Gaussische methode – Jordanië -

Op deze pagina leert u wat de Gauss-Jordan-methode is en hoe u een stelsel vergelijkingen kunt oplossen met behulp van de Gauss-methode. Daarnaast vind je ook voorbeelden en opgeloste oefeningen van systemen met de Gauss-methode zodat je deze perfect kunt oefenen en begrijpen.

Wat is de methode van Gauss?

De Gauss-Jordan-methode is een procedure die wordt gebruikt om stelsels vergelijkingen met 3 onbekenden op te lossen, dat wil zeggen als volgt:

$\left. \begin{array}{r} 3x-4y+5z=10 \\[2ex] x+5y-2z=4 \\[2ex] -x+4y+2z=-1 \end{array} \right\}$

Het doel van de methode van Gauss is om het initiële systeem van vergelijkingen om te zetten in een getrapt systeem , dat wil zeggen een systeem waarin elke vergelijking één minder onbekend heeft dan de vorige:

$\left. \begin{array}{r} a_1x+b_1y+c_1z=d_1 \\[2ex] a_2x+b_2y+c_2z=d_2 \\[2ex] a_3x+b_3y+c_3z=d_3 \end{array} \right\} \ \bm{\longrightarrow} \left. \begin{array}{r} A_1x+B_1y+C_1z=D_1 \\[2ex] B_2y+C_2z=D_2 \\[2ex] C_3z=D_3 \end{array} \right\}$

Om dit te doen, moet u echter eerst weten hoe u een stelsel vergelijkingen in matrixvorm kunt uitdrukken en welke transformaties op deze matrix zijn toegestaan . We zullen deze twee dingen dus eerder uitleggen, en daarna zullen we zien hoe we de Gauss-methode kunnen gebruiken.

Systeem-uitgebreide matrix

Voordat je ziet hoe het systeem wordt opgelost, moet je weten dat een systeem van vergelijkingen kan worden uitgedrukt in de vorm van een matrix: de coëfficiënten van de

$x}$

worden in de eerste kolom geplaatst, de coëfficiënten van de

$y}$

in de tweede kolom de coëfficiënten van de

$z$

in de derde kolom en getallen zonder onbekenden in de vierde kolom.

Bijvoorbeeld:

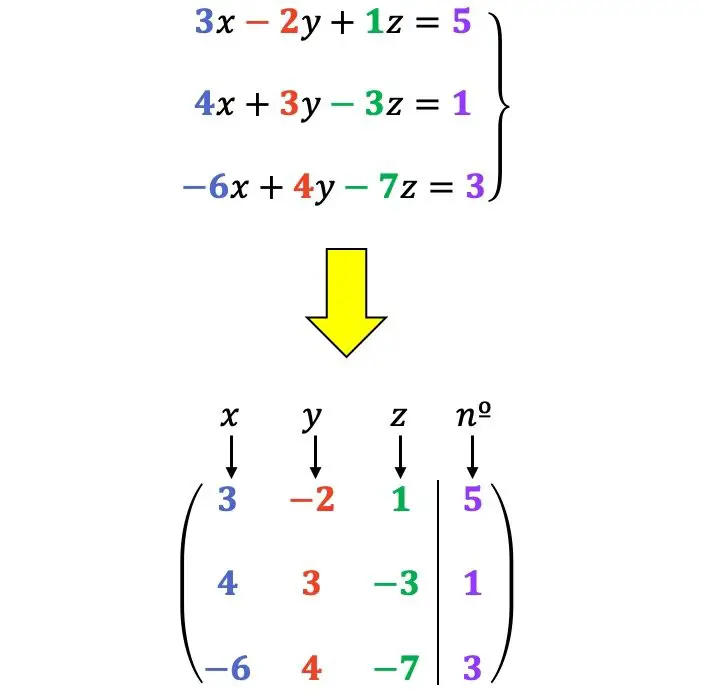
Toegestane rijtransformaties

Om het stelsel vergelijkingen om te zetten in een geschaald systeem, kan een van de volgende bewerkingen worden uitgevoerd op de matrix die bij het systeem hoort:

Wijzig de volgorde van rijen in de matrix.

We kunnen bijvoorbeeld de volgorde van regels 2 en 3 van een matrix wijzigen:

$\left( \begin{array}{ccc|c} 3 & 5 & -2 & 1 \\[2ex] -2 & 4 & -1 & 2 \\[2ex] 6 & 1 & -3 & 10 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{ f_2 \rightarrow f_3}} \\[2ex] \xrightarrow{ f_3 \rightarrow f_2}} \end{array} \left( \begin{array}{ccc|c} 3 & 5 & -2 & 1 \\[2ex] 6 & 1 & -3 & 10 \\[2ex] -2 & 4 & -1 & 2 \end{array} \right)$

Vermenigvuldig of deel alle termen in een rij met een ander getal dan 0.

We kunnen bijvoorbeeld regel 1 vermenigvuldigen met 4 en regel 3 delen met 2:

$\left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 3 & -1 & 5 & -3 \\[2ex] 2 & -4 & -2 & 6 \end{array} \right) \begin{array}{c} \xrightarrow{4 f_1} \\[2ex] \\[2ex] \xrightarrow{ f_3 / 2} \end{array} \left( \begin{array}{ccc|c} 4 & -8 & 12 & 4 \\[2ex] 3 & -1 & 5 & -3 \\[2ex] 1 & -2 & -1 & 3 \end{array} \right)$

Vervang een rij door de som van dezelfde rij plus een andere rij vermenigvuldigd met een getal.

In de volgende matrix voegen we bijvoorbeeld rij 2 toe aan rij 3, vermenigvuldigd met 1:

$\left( \begin{array}{ccc|c} -1 & -3 & 4 & 1 \\[2ex] 2 & 4 & 1 & -5 \\[2ex] 1 & -2 & 3 & -1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 + 1 \cdot f_3} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} -1 & -3 & 4 & 1 \\[2ex] 3 & 2 & 4 & -6 \\[2ex] 1 & -2 & 3 & -1 \end{array} \right)$

Hoe los je een stelsel vergelijkingen op met behulp van de Gauss-methode?

We zullen nu aan de hand van een voorbeeld de procedure bekijken voor het oplossen van een stelsel vergelijkingen met de Gauss-methode:

$\left. \begin{array}{r} -x+2y+2z=-24 \\[2ex] x+y+z=48 \\[2ex] 2x-6y+4z=12 \end{array} \right\}$

Het eerste wat u moet doen is de uitgebreide matrix van het systeem :

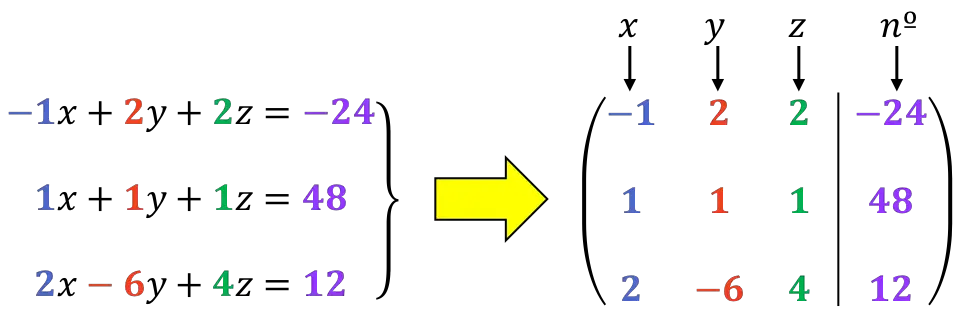
Voorbeeld van een stelsel vergelijkingen opgelost met de Gauss-methode

Zoals we later zullen zien, is het beter dat het eerste cijfer van de eerste regel een 1 is. We zullen daarom de volgorde van regels 1 en 2 veranderen:

$\left( \begin{array}{ccc|c} -1 & 2 & 2 &-24 \\[2ex] 1 & 1 & 1 & 48 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right) \begin{array}{c} \xrightarrow{ f_1 \rightarrow f_2} \\[2ex] \xrightarrow{ f_2 \rightarrow f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} \color{blue}\boxed{\color{black}1} & 1 & 1 & 48 \\[2ex] -1 & 2 & 2 &-24 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right)$

Het doel van de methode van Gauss is om de getallen onder de hoofddiagonaal 0 te maken. Dat wil zeggen, we moeten de rode cijfers naar 0 converteren:

$\left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] \color{red}\bm{-1} & 2 & 2 &-24 \\[2ex] \color{red}\bm{2} & \color{red}\bm{-6} & 4 & 12 \end{array} \right)$

Om deze getallen te elimineren, moeten we de juiste transformaties van de rijen uitvoeren.

De -1, het eerste element van de tweede rij, is bijvoorbeeld het negatief van 1, het eerste element van de eerste rij. Als we daarom de eerste regel aan de tweede regel toevoegen, wordt de -1 geëlimineerd:

$\begin{array}{lccc|c} & -1 & 2 & 2 & -24 \\ + & \phantom{-}1 & 1 & 1 & \phantom{-}48 \\ \hline & \phantom{-}0 & 3 & 3 & \phantom{-}24 \end{array} \begin{array}{l} \color{blue}\bm{\leftarrow f_2} \\ \color{blue}\bm{\leftarrow f_1} \\ \phantom{hline} \\ \end{array}$

Dus als we deze som berekenen, krijgen we de volgende matrix:

$\left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] -1 & 2 & 2 & -24 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 + f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] \color{blue}\boxed{\color{black}0} & 3 & 3 & 24 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right)$

Op deze manier zijn we erin geslaagd om -1 om te zetten in een 0.

Nu gaan we de 2 transformeren. Als je ziet, is de 2, het eerste element in de derde rij, het dubbele van 1, het eerste element in de eerste rij. Als we daarom de eerste rij vermenigvuldigd met -2 toevoegen aan de derde rij, wordt de 2 geëlimineerd:

$\begin{array}{lccc|c} & \phantom{-}2 & -6 & \phantom{-}4 & \phantom{-}12 \\ + & -2 & -2 & -2 & -96 \\ \hline & \phantom{-}0 & -8 & \phantom{-}2 & -84 \end{array} \begin{array}{l} \color{blue} \bm{\leftarrow f_3} \\ \color{blue} \bm{\leftarrow -2 f_1} \\ \phantom{hline} \\ \end{array}$

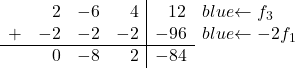
We komen dus uit op de volgende matrix:

$\left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3-2f_1} \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] \color{blue}\boxed{\color{black}0} & -8 & 2 & -84 \end{array} \right)$

Op deze manier zijn we erin geslaagd om de 2 om te zetten in een 0.

Het enige wat we nu moeten doen is de -8 omzetten naar 0. Om dit te doen, vermenigvuldigen we de derde regel met 3 en voegen we de tweede regel vermenigvuldigd met 8 toe:

$\begin{array}{lccc|r} & 0 & -24 & \phantom{2}6 & -252 \\ + & 0 & \phantom{-}24 & 24 & \phantom{-}192 \\ \hline & 0 & \phantom{-2}0 & 30 & -60 \end{array} \begin{array}{l}\color{blue}\bm{ \leftarrow 3f_3} \\\color{blue}\bm{ \leftarrow 8f_2} \\ \phantom{hline} \\ \end{array}$

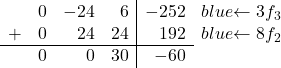
We verkrijgen daarom de volgende matrix:

$\left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] 0 & -8 & 2 & -84 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{3f_3 + 8f_2} \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] 0 & \color{blue}\boxed{\color{black}0} & 30 & -60 \end{array} \right)$

En met deze transformaties hebben we ervoor gezorgd dat alle getallen onder de hoofddiagonaal 0 zijn. Dus nu kunnen we het stelsel vergelijkingen oplossen.

We moeten nu de matrix omzetten in een systeem van vergelijkingen met onbekenden . Om dit te doen, onthoud dat de eerste kolom overeenkomt met de

$x$

, de tweede kolom van

$y$

, de derde kolom van

$z$

en de laatste kolom zijn de getallen zonder onbekenden:

$\left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] 0 & 0 & 30 & -60 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 1x+1y+1z=48 \\[2ex] 3y+3z=24 \\[2ex] 30z=-60 \end{array} \right\}$

En ten slotte moeten we, om het systeem op te lossen, de onbekenden van de vergelijkingen van onder naar boven oplossen. Omdat de laatste vergelijking slechts één onbekende heeft, kunnen we deze oplossen en de waarde ervan vinden:

$30z=-60$

$z = \cfrac{-60}{30}$

$\bm{z=-2}$

Nu we weten wat z is, kunnen we, als we de waarde ervan in de tweede vergelijking invullen, de waarde van vinden

$y$

$3y+3z=24 \ \xrightarrow{z \ = \ -2} \ 3y+3(-2)=24$

$3y-6=24$

$3y=24+6$

$3y=30$

$y=\cfrac{30}{3}$

$\bm{y=10}$

En we doen hetzelfde met de eerste vergelijking: we vervangen de waarden van de andere onbekenden en we wissen

$x$

$1x+1y+1z=48 \ \xrightarrow{y \ = \ 10 \ ; \ z \ = \ -2} \ 1x+1(10)+1(-2)=48$

$x+10-2=48$

$x=48-10+2$

$\bm{x=40}$

De oplossing van het stelsel vergelijkingen is daarom:

$\bm{x=40} \quad \bm{y=10} \quad \bm{z=-2}$

Problemen van stelsels vergelijkingen opgelost volgens de Gauss-Jordan-methode

Oefening 1

Los het volgende stelsel vergelijkingen op met behulp van de Gauss-methode:

$\left. \begin{array}{r} x+y-z=2 \\[2ex] x-2y+3z=0 \\[2ex] 2x-y+3z=3 \end{array} \right\}$

zie oplossing

Het eerste dat we moeten doen is de uitgebreide matrix van het systeem:

$\left. \begin{array}{r} x+y-z=2 \\[2ex] x-2y+3z=0 \\[2ex] 2x-y+3z=3 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 1 & 1 & -1 & 2 \\[2ex] 1 & -2 & 3 & 0 \\[2ex] 2 & -1 & 3 & 3 \end{array} \right)$

Nu moeten we alle getallen onder de hoofdarray 0 maken.

We voeren daarom rijbewerkingen uit om de laatste twee termen van de eerste kolom te annuleren:

$\left( \begin{array}{ccc|c}1 & 1 & -1 & 2 \\[2ex] 1 & -2 & 3 & 0 \\[2ex] 2 & -1 & 3 & 3 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -f_1} \\[2ex] \xrightarrow{f_3-2f_1} & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & -1 & 2 \\[2ex] 0 & -3 & 4 & -2 \\[2ex] 0 & -3 & 5 & -1 \end{array} \right)$

Nu verwijderen we het laatste element uit de tweede kolom:

$\left( \begin{array}{ccc|c}1 & 1 & -1 & 2 \\[2ex] 0 & -3 & 4 & -2 \\[2ex] 0 & -3 & 5 & -1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3-f_2} & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & -1 & 2 \\[2ex] 0 & -3 & 4 & -2 \\[2ex] 0 & 0 & 1 & 1 \end{array} \right)$

Zodra alle getallen onder de hoofddiagonaal 0 zijn, kunnen we nu het stelsel vergelijkingen oplossen. Om dit te doen, drukken we de matrix opnieuw uit in de vorm van een stelsel van vergelijkingen met onbekenden:

$\left( \begin{array}{ccc|c} 1 & 1 & -1 & 2 \\[2ex] 0 & -3 & 4 & -2 \\[2ex] 0 & 0 & 1 & 1 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x+y-z=2 \\[2ex] -3y+4z=-2 \\[2ex] 1z=1 \end{array} \right\}$

En we lossen de onbekenden van de vergelijkingen van onder naar boven op. We lossen eerst de laatste vergelijking op:

$1z= 1$

$z=\bm{1}$

Nu vervangen we de waarde van z in de tweede vergelijking om de waarde van y te vinden:

$-3y+4z=-2 \ \xrightarrow{z \ = \ 1} \ -3y+4(1)=-2$

$-3y+4=-2$

$-3y=-2-4$

$-3y=-6$

$y=\cfrac{-6}{-3} = \bm{2}$

En we doen hetzelfde met de eerste vergelijking: we vervangen de waarden van de andere onbekenden en we lossen op voor x:

$x+y-z=2 \ \xrightarrow{y \ = \ 2 \ ; \ z \ = \ 1} \ x+(2)-(1)=2$

$x+1=2$

$x=2-1$

$\bm{x=1}$

De oplossing van het stelsel vergelijkingen is daarom:

$\bm{x=1} \qquad \bm{y=2} \qquad \bm{z=1}$

Oefening 2

Vind de oplossing voor het volgende stelsel vergelijkingen met behulp van de Gauss-methode:

$\left. \begin{array}{r} 2x+y+2z=-3 \\[2ex] x+3y+2z=5 \\[2ex] 4x+2y-z=-1 \end{array} \right\}$

zie oplossing

Het eerste dat we moeten doen is de uitgebreide matrix van het systeem:

$\left. \begin{array}{r} 2x+y+2z=-3 \\[2ex] x+3y+2z=5 \\[2ex] 4x+2y-z=-1 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 2 & 1 & 2 & -3 \\[2ex] 1 & 3 & 2 & 5 \\[2ex] 4 & 2 & -1 & -1 \end{array} \right)$

Om de Gauss-methode toe te passen is het eenvoudiger als het eerste getal op de eerste regel een 1 is. We zullen daarom de volgorde van regels 1 en 2 veranderen:

$\left( \begin{array}{ccc|c}2 & 1 & 2 & -3 \\[2ex] 1 & 3 & 2 & 5 \\[2ex] 4 & 2 & -1 & -1 \end{array} \right) \begin{array}{c} \xrightarrow{f_1\rightarrow f_2} \\[2ex] \xrightarrow{f_2\rightarrow f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c}1 & 3 & 2 & 5 \\[2ex] 2 & 1 & 2 & -3 \\[2ex] 4 & 2 & -1 & -1\end{array} \right)$

Nu moeten we alle getallen onder de hoofdarray 0 maken.

We voeren dus rijbewerkingen uit om de laatste twee elementen van de eerste kolom te vervangen:

$\left( \begin{array}{ccc|c} 1 & 3 & 2 & 5 \\[2ex] 2 & 1 & 2 & -3 \\[2ex] 4 & 2 & -1 & -1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -2f_1} \\[2ex] \xrightarrow{f_3-4f_1} & \end{array} \left( \begin{array}{ccc|c} 1 & 3 & 2 & 5 \\[2ex] 0 & -5 & -2 & -13 \\[2ex] 0 & -10 & -9 & -21 \end{array} \right)$

Nu converteren we het laatste element van de tweede kolom naar nul:

$\left( \begin{array}{ccc|c}1 & 3 & 2 & 5 \\[2ex] 0 & -5 & -2 & -13 \\[2ex] 0 & -10 & -9 & -21\end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3-2f_2} & \end{array} \left( \begin{array}{ccc|c} 1 & 3 & 2 & 5 \\[2ex] 0 & -5 & -2 & -13 \\[2ex] 0 & 0 & -5 & 5 \end{array} \right)$

Zodra alle getallen onder de hoofddiagonaal 0 zijn, kunnen we het stelsel vergelijkingen oplossen. Om dit te doen, drukken we de matrix opnieuw uit in de vorm van een stelsel van vergelijkingen met onbekenden:

$\left( \begin{array}{ccc|c} 1 & 3 & 2 & 5 \\[2ex] 0 & -5 & -2 & -13 \\[2ex] 0 & 0 & -5 & 5 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x+3y+2z=5 \\[2ex] -5y-2z=-13 \\[2ex] -5z=5 \end{array} \right\}$

En we lossen de onbekenden van de vergelijkingen van onder naar boven op. We lossen eerst de laatste vergelijking op:

$-5z= 5$

$z=\cfrac{5}{-5}=\bm{-1}$

Nu vervangen we de waarde van z in de tweede vergelijking om de waarde van y te vinden:

$-5y-2z=-13 \ \xrightarrow{z \ = \ -1} \ -5y-2(-1)=-13$

$-5y+2=-13$

$-5y=-13-2$

$-5y=-15$

$y=\cfrac{-15}{-5} = \bm{3}$

En we doen hetzelfde met de eerste vergelijking: we vervangen de waarden van de andere onbekenden en we lossen op voor x:

$x+3y+2z=5 \ \xrightarrow{y \ = \ 3 \ ; \ z \ = \ -1} \ x+3(3)+2(-1)=5$

$x+9-2=5$

$x=5-9+2$

$\bm{x=-2}$

De oplossing van het stelsel vergelijkingen is daarom:

$\bm{x=-2} \qquad \bm{y=3} \qquad \bm{z=-1}$

Oefening 3

Bereken de oplossing van het volgende stelsel vergelijkingen volgens de Gauss-methode:

$\left. \begin{array}{r} 2x+3y+z=-1 \\[2ex] 6x+4y+4z=0 \\[2ex] -4x+2y-z=5 \end{array} \right\}$

zie oplossing

Het eerste dat we moeten doen is de uitgebreide matrix van het systeem:

$\left. \begin{array}{r} 2x+3y+z=-1 \\[2ex] 6x+4y+4z=0 \\[2ex] -4x+2y-z=5\end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 6 & 4 & 4 & 0 \\[2ex] -4 & 2 & -1 & 5 \end{array} \right)$

Nu moeten we alle getallen onder de bovenliggende array 0 maken.

We voeren dus rijbewerkingen uit om de laatste twee elementen van de eerste kolom te vervangen:

$\left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 6 & 4 & 4 & 0 \\[2ex] -4 & 2 & -1 & 5\end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -3f_1} \\[2ex] \xrightarrow{f_3+2f_1} & \end{array} \left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 0 & -5 & 1 & 3 \\[2ex] 0 & 8 & 1 & 3\end{array} \right)$

Nu converteren we het laatste element van de tweede kolom naar nul:

$\left( \begin{array}{ccc|c}2 & 3 & 1 & -1 \\[2ex] 0 & -5 & 1 & 3 \\[2ex] 0 & 8 & 1 & 3\end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{5f_3+8f_2} & \end{array} \left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 0 & -5 & 1 & 3 \\[2ex] 0 & 0 & 13 & 39 \end{array} \right)$

$\left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 0 & -5 & 1 & 3 \\[2ex] 0 & 0 & 13 & 39\end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 2x+3y+1z=-1 \\[2ex] -5y+z=3 \\[2ex] 13z=39 \end{array} \right\}$

En we lossen de onbekenden van de vergelijkingen van onder naar boven op. We lossen eerst de laatste vergelijking op:

$13z= 39$

$z=\cfrac{39}{13}=\bm{3}$

Nu vervangen we de waarde van z in de tweede vergelijking om de waarde van y te vinden:

$-5y+z=3 \ \xrightarrow{z \ = \ 3} \ -5y+(3)=3$

$-5y=3-3$

$-5y=0$

$y=\cfrac{0}{-5} = \bm{0}$

En we doen hetzelfde met de eerste vergelijking: we vervangen de waarden van de andere onbekenden en we lossen op voor x:

$2x+3y+1z=-1 \ \xrightarrow{y \ = \ 0 \ ; \ z \ = \ 3} \ 2x+3(0)+1(3)=-1$

$2x+0+3=-1$

$2x=-1-3$

$2x=-4$

$x=\cfrac{-4}{2}=\bm{-2}$

De oplossing van het stelsel vergelijkingen is daarom:

$\bm{x=-2} \qquad \bm{y=0} \qquad \bm{z=3}$

Oefening 4

Los het volgende stelsel vergelijkingen met 3 onbekenden op met behulp van de Gauss-methode:

$\left. \begin{array}{r} 2x-6=4y+6z \\[2ex] -y-3z=1-3x \\[2ex] -4x-y=6-3z \end{array} \right\}$

zie oplossing

Voordat we de methode van Gauss toepassen, moeten we het stelsel vergelijkingen zo rangschikken dat alle onbekenden zich aan de linkerkant van de vergelijking bevinden en de getallen aan de rechterkant:

$\left. \begin{array}{r}2x-6=4y+6z \\[2ex] -y-3z=1-3x \\[2ex] -4x-y=6-3z \end{array} \right\} \longrightarrow \left. \begin{array}{r} 2x-4y-6z=6 \\[2ex] 3x-y-3z=1 \\[2ex] -4x-y+3z=6\end{array} \right\}$

Zodra het systeem is besteld, construeren we de ontwikkelde matrix van het systeem:

$\left. \begin{array}{r} 2x-4y-6z=6 \\[2ex] 3x-y-3z=1 \\[2ex] -4x-y+3z=6 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 2 & -4 & -6 & 6 \\[2ex] 3 & -1 & -3 & 1 \\[2ex] -4 & -1 & 3 & 6 \end{array} \right)$

Omdat alle getallen in de eerste rij even zijn, delen we, voordat we met de rijen gaan werken, de eerste rij door 2. Omdat dit de berekeningen eenvoudiger maakt:

$\left( \begin{array}{ccc|c}2 & -4 & -6 & 6 \\[2ex] 3 & -1 & -3 & 1 \\[2ex] -4 & -1 & 3 & 6 \end{array} \right) \begin{array}{c} \xrightarrow{f_1/2} \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|c}1 & -2 & -3 & 3 \\[2ex] 3 & -1 & -3 & 1 \\[2ex] -4 & -1 & 3 & 6\end{array} \right)$

Nu moeten we alle getallen onder de hoofdarray 0 maken.

We voeren dus rijbewerkingen uit om de laatste twee elementen van de eerste kolom te vervangen:

$\left( \begin{array}{ccc|c} 1 & -2 & -3 & 3 \\[2ex] 3 & -1 & -3 & 1 \\[2ex] -4 & -1 & 3 & 6 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -3f_1} \\[2ex] \xrightarrow{f_3+4f_1} & \end{array} \left( \begin{array}{ccc|c} 1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & -9 & -9 & 18\end{array} \right)$

Omdat alle getallen in de laatste regel een veelvoud van 9 zijn, delen we dit net als voorheen door 9 om de berekeningen eenvoudiger te maken:

$\left( \begin{array}{ccc|c}1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & -9 & -9 & 18 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex]\xrightarrow{f_3/9} & \end{array} \left( \begin{array}{ccc|c}1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & -1 & -1 & 2\end{array} \right)$

Nu converteren we het laatste element van de tweede kolom naar nul:

$\left( \begin{array}{ccc|c}1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & -1 & -1 & 2\end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{5f_3+f_2} & \end{array} \left( \begin{array}{ccc|c} 1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & 0 & 1 & 2 \end{array} \right)$

$\left( \begin{array}{ccc|c} 1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & 0 & 1 & 2 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x-2y-3z=3 \\[2ex] 5y+6z=-8 \\[2ex] 1z=2 \end{array} \right\}$