Jacobiaanse en Jacobiaanse matrix

Op deze pagina vind je wat de Jacobiaanse matrix is en hoe je deze kunt berekenen aan de hand van een voorbeeld. Daarnaast heb je verschillende opgeloste oefeningen op Jacobiaanse matrices zodat je kunt oefenen. Je zult ook zien waarom de determinant van de Jacobiaanse matrix, de Jacobiaan, zo belangrijk is. Ten slotte leggen we de relaties uit die deze matrix onderhoudt met andere operaties en de toepassingen die deze heeft.

Wat is de Jacobiaanse matrix?

De definitie van de Jacobiaanse matrix is als volgt:

De Jacobiaanse matrix is een matrix gevormd door de partiële afgeleiden van de eerste orde van een functie.

De formule voor de Jacobiaanse matrix is daarom als volgt:

Daarom zullen Jacobiaanse matrices altijd evenveel rijen hebben als scalaire functies

$(f_1,f_2,\ldots ,f_m)$

hebben de functie, en het aantal kolommen komt overeen met het aantal variabelen

$(x_1, x_2, \ldots , x_n).$

Aan de andere kant staat deze matrix ook bekend als Jacobiaanse differentiële kaart of Jacobiaanse lineaire kaart . Soms wordt het zelfs met de letter D geschreven in plaats van de letter J:

$\displaystyle J_f = D_f$

Uit curiositeit is de Jacobiaanse matrix vernoemd naar Carl Gustav Jacobi, een belangrijke 19e-eeuwse wiskundige en professor die belangrijke bijdragen leverde aan de wereld van de wiskunde, vooral op het gebied van de lineaire algebra.

Voorbeeld van het berekenen van de Jacobiaanse matrix

Zodra we het concept van de Jacobiaanse matrix zien, zullen we stap voor stap zien hoe deze wordt berekend aan de hand van een voorbeeld:

Bepaal de Jacobiaanse matrix op punt (1,2) van de volgende functie:

$\displaystyle f(x,y)= (x^4 +3y^2x \ , \ 5y^2-2xy+1)$

Het eerste dat we moeten doen is alle partiële afgeleiden van de eerste orde van de functie berekenen:

$\displaystyle \cfrac{\partial f_1}{\partial x} = 4x^3+3y^2$

$\displaystyle \cfrac{\partial f_1}{\partial y} = 6yx$

$\displaystyle \cfrac{\partial f_2}{\partial x} = -2y$

$\displaystyle \cfrac{\partial f_2}{\partial y} = 10y-2x$

Nu passen we de Jacobiaanse matrixformule toe. In dit geval heeft de functie twee variabelen en twee scalaire functies, dus de Jacobiaanse matrix zal een vierkante matrix zijn met dimensie 2×2:

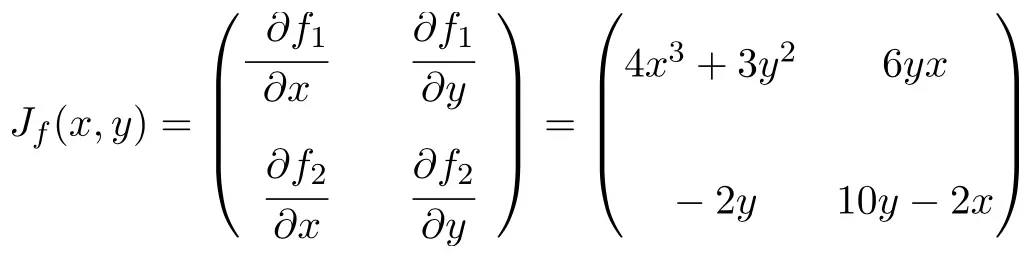
Zodra we de uitdrukking voor de Jacobiaanse matrix hebben, evalueren we deze op punt (1,2):

$\displaystyle J_f(1,2)=\begin{pmatrix} 4\cdot 1^3+3\cdot 2^2 & 6\cdot 2 \cdot 1 \\[3ex] -2\cdot 2 & 10\cdot 2-2 \cdot 1 \end{pmatrix}$

En ten slotte voeren we de handelingen uit en verkrijgen we de oplossing:

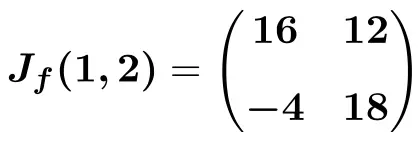
voorbeeld van het berekenen van de Jacobiaanse matrix

Zodra je hebt gezien hoe je de Jacobiaanse matrix van een functie kunt vinden, laten we je verschillende oefeningen stap voor stap oplossen, zodat je kunt oefenen.

Problemen van Jacobiaanse matrices opgelost

Oefening 1

Zoek de Jacobiaanse matrix op het punt (0,-2) van de volgende vectorfunctie in 2 variabelen:

$\displaystyle f(x,y)= (e^{xy}+y \ , \ y^2x)$

zie oplossing

De functie heeft twee variabelen en twee scalaire functies, dus de Jacobiaanse matrix zal een vierkante matrix zijn met de grootte 2×2:

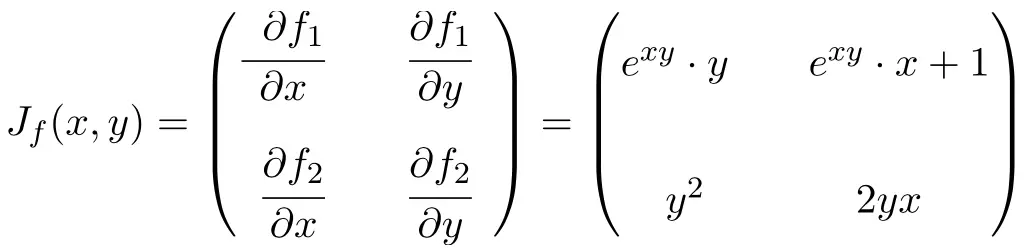
Nadat we de uitdrukking voor de Jacobiaanse matrix hebben berekend, evalueren we deze op het punt (0,-2):

$\displaystyle J_f(0,-2)=\begin{pmatrix}e^{0\cdot (-2)}\cdot (-2)\phantom{5} & \phantom{5}e^{0\cdot (-2)} \cdot 0 +1 \\[4ex](-2)^2 & 2\cdot (-2) \cdot 0 \end{pmatrix}$

En ten slotte voeren we de bewerkingen uit en verkrijgen we het resultaat:

$\displaystyle \bm{J_f(0,-2)}=\begin{pmatrix} \bm{-2} & \bm{1} \\[1.5ex] \bm{4} & \bm{0} \end{pmatrix}$

Oefening 2

Bereken de Jacobiaanse matrix op het punt (2,-1) van de volgende functie met 2 variabelen:

$\displaystyle f(x,y)= (x^3y^2 - 5x^2y^2 \ , \ y^6-3y^3x+7)$

zie oplossing

In dit geval heeft de functie twee variabelen en twee scalaire functies, dus de Jacobiaanse matrix zal een vierkante matrix van orde 2 zijn:

$\displaystyle J_f(x,y)=\begin{pmatrix}\cfrac{\phantom{5}\partial f_1}{\partial x}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial y}\phantom{5} \\[3ex] \cfrac{\partial f_2}{\partial x} & \cfrac{\partial f_2}{\partial y}\end{pmatrix} = \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}}3x^2y^2-10xy^2& 2x^3y-10x^2y \\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} -3y^3 & 6y^5-9y^2x \end{pmatrix}$

Zodra we de uitdrukking voor de Jacobiaanse matrix hebben gevonden, evalueren we deze op punt (2,-1):

$\displaystyle J_f(2,-1)=\begin{pmatrix} 3\cdot 2^2\cdot (-1)^2-10\cdot 2 \cdot (-1)^2\phantom{5} & \phantom{5}2\cdot 2^3\cdot (-1)-10\cdot 2^2\cdot (-1) \\[4ex] -3(-1)^3 & 6\cdot (-1)^5-9\cdot (-1)^2\cdot 2 \end{pmatrix}$

En ten slotte voeren we de bewerkingen uit en verkrijgen we het resultaat:

$\displaystyle \bm{J_f(1,2)}=\begin{pmatrix} \bm{-8} & \bm{24} \\[1.5ex] \bm{3} & \bm{-24} \end{pmatrix}$

Oefening 3

Bepaal de Jacobiaanse matrix op het punt (2,-2,2) van de volgende functie met 3 variabelen:

$\displaystyle f(x,y,z)= \left(z\tan (x^2-y^2) \ , \ xy\ln \left( \frac{z}{2} \right)\right)$

zie oplossing

In dit geval heeft de functie drie variabelen en twee scalaire functies, daarom zal de Jacobiaanse matrix een rechthoekige matrix zijn met dimensie 2×3:

$\displaystyle J_f(x,y,z)= \begin{pmatrix}\cfrac{\phantom{5}\partial f_1}{\partial x}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial y}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial z}\phantom{5} \\[3ex] \cfrac{\partial f_2}{\partial x} & \cfrac{\partial f_2}{\partial y} &\cfrac{\partial f_2}{\partial z}\end{pmatrix}$

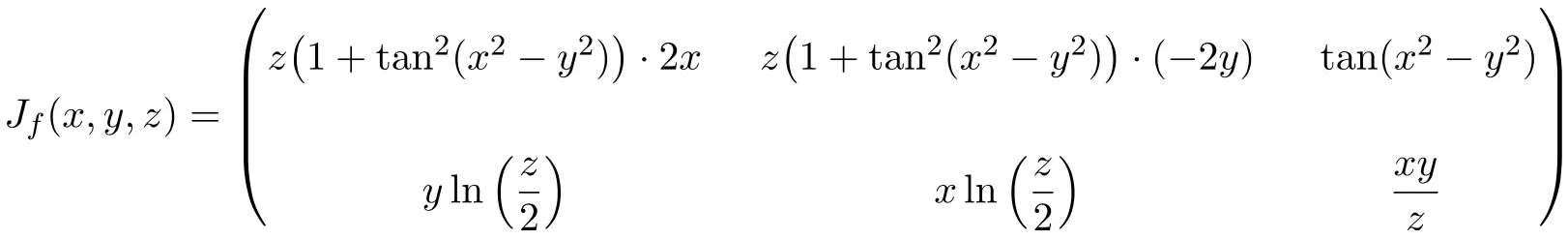
Jacobiaanse matrix loste oefening van 3 variabelen op

Zodra we de uitdrukking voor de Jacobiaanse matrix hebben, evalueren we deze op het punt (2,-2,2):

$\displaystyle J_f(2,-2,2)= \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}}2\bigl(1+\tan^2 (2^2-(-2)^2)\bigr) \cdot 2\cdot 2 & 2\bigl(1+\tan^2 (2^2-(-2)^2)\bigr) \cdot (-2\cdot (-2)) & \tan (2^2-(-2)^2)\\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} \displaystyle -2\ln \left( \frac{2}{2} \right) & \displaystyle 2\ln \left( \frac{2}{2} \right) &\displaystyle \frac{2\cdot (-2)}{2} \right)\end{pmatrix}$

Wij voeren de berekeningen uit:

$\displaystyle J_f(2,-2,2)= \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}}2\bigl(1+\tan^2 (0)\bigr) \cdot 4 \phantom{5} & 2\bigl(1+\tan^2 (0)\bigr) \cdot 4 & \phantom{5}\tan (0)\\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} -2\cdot 0 & 2\cdot 0 &-2 \right)\end{pmatrix}$

En we blijven doorgaan totdat het niet langer eenvoudiger kan:

$\displaystyle \bm{J_f(2,-2,2)=} \begin{pmatrix}\bm{8} & \bm{8} & \bm{0} \\[2ex] \bm{0} & \bm{0} &\bm{-2} \right)\end{pmatrix}$

Oefening 4

Bepaal de Jacobiaanse matrix op het punt

$(\pi, \pi)$

van de volgende multivariabele functie:

$\displaystyle f(x,y)= \left( \frac{\cos (x-y)}{x} \ , \ e^{x^2-y^2} \ , \ x^3\sin (2y) \right)$

zie oplossing

In dit geval heeft de functie twee variabelen en drie scalaire functies, daarom zal de Jacobiaanse matrix een rechthoekige matrix zijn met dimensie 3×2:

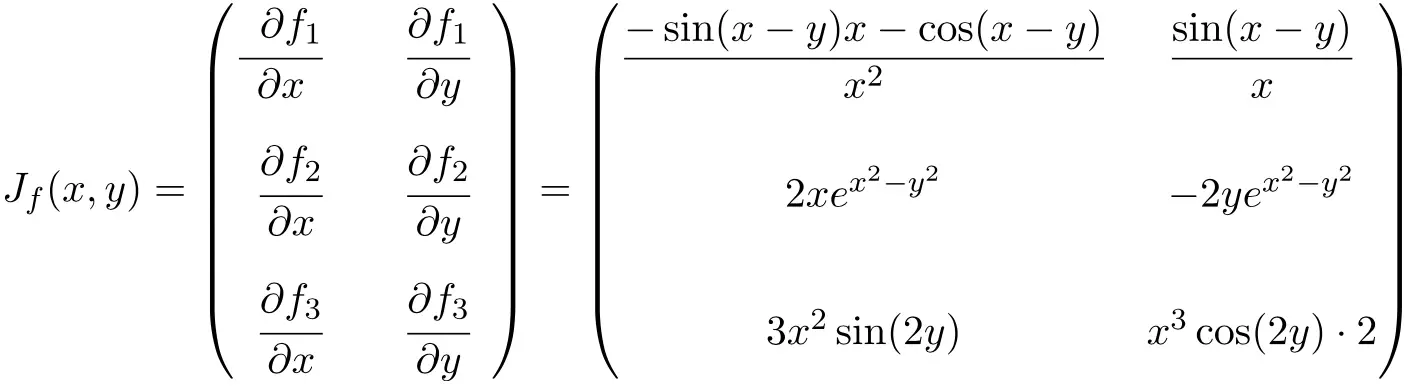
oefening stap voor stap opgelost volgens de Jacobiaanse matrix

Zodra we de uitdrukking voor de Jacobiaanse matrix hebben, evalueren we deze tot op het punt

$(\pi, \pi):$

$\displaystyle J_f(\pi,\pi)= \begin{pmatrix} \displaystyle \vphantom{\cfrac{\partial f_3}{\partial y}}\frac{-\sin(\pi-\pi)\pi-\cos(\pi-\pi)}{\pi^2} & \displaystyle\frac{\sin (\pi- \pi)}{\pi} \\[3ex] \vphantom{\cfrac{\partial f_3}{\partial y}}2\pi e^{\pi^2-\pi^2} & -2\pi e^{\pi^2-\pi^2} \\[3ex] \vphantom{\cfrac{\partial f_3}{\partial y}} 3\pi^2\sin(2\pi) & \pi^3 \cos(2\pi)\cdot 2 \end{pmatrix}$

Wij voeren de bewerkingen uit:

$\displaystyle J_f(\pi,\pi)= \begin{pmatrix} \displaystyle \vphantom{\cfrac{\partial f_3}{\partial y}}\displaystyle\frac{-0-1}{\pi^2} & \displaystyle\frac{0}{\pi} \\[3ex] \vphantom{\cfrac{\partial f_3}{\partial y}}2\pi e^{0} & -2\pi e^{0} \\[3ex] \vphantom{\cfrac{\partial f_3}{\partial y}} 3\pi^2\cdot 0 & \pi^3 \cdot 1 \cdot 2 \end{pmatrix}$

De Jacobiaanse matrix van de vectorfunctie op het beschouwde punt is dus de volgende waarde:

$\displaystyle \bm{J_f(\pi,\pi)=} \begin{pmatrix}\displaystyle -\frac{\bm{1}}{\bm{\pi^2}} & \bm{0} \\[3ex] \bm{2\pi} & \bm{-2\pi}\\[3ex]\bm{0} & \bm{2\pi^3} \right)\end{pmatrix}$

Oefening 5

Bereken de Jacobiaanse matrix op het punt

$(3,0,\pi)$

van de volgende functie met 3 variabelen:

$\displaystyle f(x,y,z)= \left(xe^{2y}\cos(-z) \ , \ (y-2)^3\cdot \sin\left(\frac{z}{2}\right) \ , \ e^{2y}\cdot \ln\left(\frac{x}{3}\right) \right)$

zie oplossing

In dit geval bestaat de functie uit drie variabelen en drie scalaire functies, daarom zal de Jacobiaanse matrix een vierkante matrix zijn met dimensie 3×3:

$\displaystyle J_f(x,y,z)=\begin{pmatrix}\phantom{5}\cfrac{\partial f_1}{\partial x}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial y}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial z}\phantom{5} \\[3ex] \cfrac{\partial f_2}{\partial x} & \cfrac{\partial f_2}{\partial y} & \cfrac{\partial f_2}{\partial z} \\[3ex] \cfrac{\partial f_3}{\partial x} & \cfrac{\partial f_3}{\partial y} & \cfrac{\partial f_3}{\partial z}\end{pmatrix}$

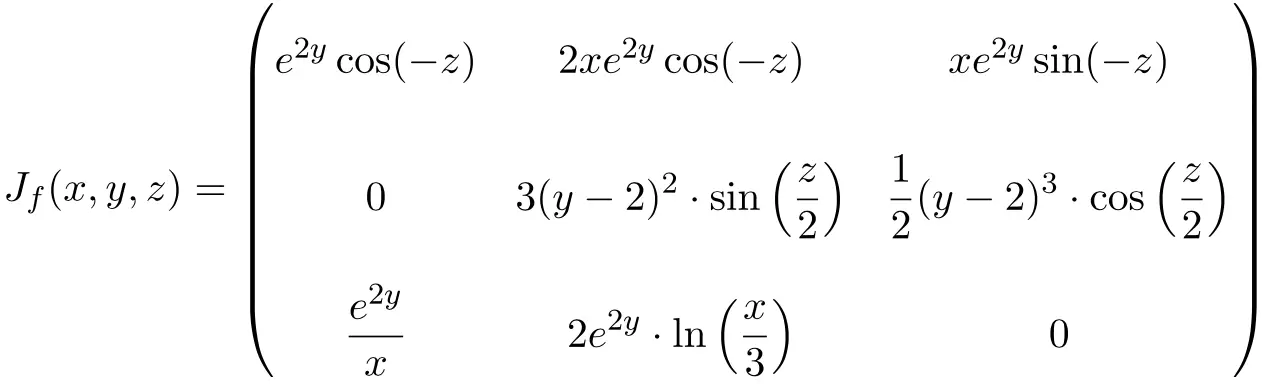
Opgeloste oefening van 3x3 Jacobiaanse matrix met 3 variabelen

Zodra we de Jacobiaanse matrix hebben gevonden, evalueren we deze op het punt

$(3,0,\pi):$

$\displaystyle J_f(3,0,\pi)= \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}} e^{2\cdot 0}\cos(-\pi) & 2\cdot 3e^{2\cdot 0}\cos(-\pi) & 3e^{2\cdot 0}\sin(-\pi) \\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} 0 & \displaystyle 3(0-2)^2\cdot \sin\left(\frac{\pi}{2}\right) & \displaystyle\frac{1}{2}(0-2)^3\cdot \cos\left(\frac{\pi}{2}\right)\\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}}\displaystyle\frac{e^{2\cdot 0}}{3} &\displaystyle 2e^{2\cdot 0}\cdot \ln\left(\frac{3}{3}\right) & 0\end{pmatrix}$

We berekenen de bewerkingen:

$\displaystyle J_f(3,0,\pi)= \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}} 1\cdot (-1) & 6\cdot 1\cdot (-1) & 3\cdot 1 \cdot 0 \\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} 0 & \displaystyle 3\cdot 4 \cdot 1 & \displaystyle\frac{1}{2}\cdot (-8)\cdot 0\\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}}\displaystyle\frac{1}{3} &\displaystyle 2\cdot 1\cdot 0 & 0\end{pmatrix}$

En het resultaat van de Jacobiaanse matrix op dit punt is:

$\displaystyle \bm{J_f(3,0,\pi)=} \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}} \bm{-1} & \bm{-6} & \phantom{-}\bm{0} \\[2ex] \bm{0} & \bm{12} & \displaystyle \bm{0} \\[2ex] \displaystyle \frac{\bm{1}}{\bm{3}} &\bm{0}& \bm{0}\end{pmatrix}$

Determinant van de Jacobiaanse matrix: de Jacobiaan

De determinant van de Jacobiaanse matrix wordt Jacobiaanse determinant of Jacobiaan genoemd. Er moet rekening mee worden gehouden dat de Jacobiaan alleen kan worden berekend als de functie hetzelfde aantal variabelen heeft als de scalaire functies, omdat de Jacobiaanse matrix dan hetzelfde aantal rijen als kolommen zal hebben en daarom een vierkant zal zijn. Matrix. .

Jacobiaans voorbeeld

Laten we een voorbeeld bekijken van het berekenen van de Jacobiaanse determinant van een functie met twee variabelen:

$\displaystyle f(x,y)= (x^2-y^2 \ , \ 2xy)$

We berekenen eerst de Jacobiaanse matrix van de functie:

$\displaystyle J_f(x,y)=\begin{pmatrix}\cfrac{\phantom{5}\partial f_1}{\partial x}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial y}\phantom{5} \\[3ex] \cfrac{\partial f_2}{\partial x} & \cfrac{\partial f_2}{\partial y}\end{pmatrix} = \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}}2x \phantom{5}& -2y \\[2ex] \vphantom{\cfrac{\partial f_2}{\partial x}} 2y & 2x \end{pmatrix}$

En nu lossen we de determinant van de 2×2 matrix op:

$\displaystyle \text{det}\bigl(J_f(x,y)\bigr) =\begin{vmatrix} 2x&-2y \\[2ex] 2y & 2x \end{vmatrix} = \bm{4x^2+4y^2}$

De Jacobiaan en de invertibiliteit van een functie

Nu je het concept van de Jacobiaan hebt gezien, heb je waarschijnlijk gedacht… nou, wat heeft het voor zin?

Welnu, het belangrijkste gebruik van de Jacobiaan is om te bepalen of een functie kan worden omgekeerd. De inverse functiestelling zegt dat als de determinant van de Jacobiaanse matrix (de Jacobiaan) verschillend is van 0, dit betekent dat deze functie inverteerbaar is.

$\displaystyle \text{det}\bigl(J_f\bigr) \neq 0 \ \longrightarrow \ \exists \ f^{-1}$

Opgemerkt moet worden dat deze voorwaarde noodzakelijk maar niet voldoende is, dat wil zeggen dat als de determinant niet nul is, we kunnen beweren dat de matrix kan worden omgekeerd. Als de determinant echter 0 is, kunnen we niet weten of de matrix kan worden omgekeerd. functie heeft een inverse of Nee.

In het eerder geziene voorbeeld van hoe je de Jacobiaan van een functie kunt vinden, geeft de determinant bijvoorbeeld

$4x^2+4y^2$

. In dit geval kunnen we beweren dat de functie altijd kan worden omgekeerd, behalve op het punt (0,0), aangezien dit punt het enige is waar de Jacobiaanse determinant gelijk is aan nul en we daarom niet weten of de inverse functie bestaat op dit punt.

Relatie van Jacobiaanse matrix met andere bewerkingen

De Jacobiaanse matrix houdt verband met de gradiënt en de Hessische matrix van een functie:

Helling

Als de functie een scalaire functie is, zal de Jacobiaanse matrix een rijmatrix zijn die equivalent zal zijn aan de gradiënt :

$\displaystyle f: \mathbb{R}^n \to \mathbb{R}$

$\displaystyle J_f = \nabla f = \begin{pmatrix}\phantom{5} \cfrac{\partial f}{\partial x_1} \phantom{5}& \cfrac{\partial f}{\partial x_2}& \dots & \cfrac{\partial f}{\partial x_n}\phantom{5} \end{pmatrix}$

Hessische matrix

De Jacobiaanse matrix van de gradiënt van een functie is gelijk aan de Hessische matrix :

$\displaystyle H_f = J(\nabla f)$

De Hessiaan is een zeer belangrijke matrix voor het afleiden van functies met meer dan één variabele, omdat deze wordt gevormd door de tweede afgeleide van de functie. In feite zou je kunnen zeggen dat de Hessische matrix de continuïteit is van de Jacobiaanse matrix. Maar het is zo belangrijk dat we een hele pagina hebben waarop dit in detail wordt uitgelegd. Als je dus precies wilt weten wat deze matrix is en waarom deze zo bijzonder is, kun je op de link klikken.

Toepassingen van de Jacobiaanse matrix

Naast het nut dat we hebben gezien van de Jacobiaan, die bepaalt of een functie inverteerbaar is, heeft de Jacobiaanmatrix nog andere toepassingen.

De Jacobiaanse matrix wordt gebruikt om de kritische punten van een multivariate functie te berekenen, die vervolgens via de Hessische matrix worden geclassificeerd in maxima, minima of zadelpunten. Om de kritische punten te vinden, moet je de Jacobiaanse matrix van de functie berekenen, deze gelijkstellen aan 0 en de resulterende vergelijkingen oplossen.

$\displaystyle J_f(x)=0$

Bovendien wordt een andere toepassing van de Jacobiaanse matrix gevonden in de integratie van functies met meer dan één variabele, dat wil zeggen in dubbele, drievoudige integralen, enz. Omdat de determinant van de Jacobiaanse matrix een verandering van variabele in meerdere integralen mogelijk maakt volgens de volgende formule:

$\displaystyle x=T(x^*)$

$\displaystyle \int_\Omega f(x)dx=\int_{\Omega^*} f\bigl(T(x^*)\bigr)\cdot \begin{vmatrix} \text{det}\bigl(JT(x^*)\bigr)\end{vmatrix} dx^*$

Waarbij T de variabele veranderingsfunctie is die de oorspronkelijke variabelen relateert aan de nieuwe.

Ten slotte wordt de Jacobiaanse matrix ook gebruikt om een lineaire benadering van elke functie te maken

$f$

rond een punt

$p$

$\displaystyle f(x) \approx f(p) + J_f(p)(x-p)$

Jacobiaanse en jacobiaanse matrix

Wat is de Jacobiaanse matrix?

Voorbeeld van het berekenen van de Jacobiaanse matrix

Problemen van Jacobiaanse matrices opgelost

Oefening 1

Oefening 2

Oefening 3

Oefening 4

Oefening 5

Determinant van de Jacobiaanse matrix: de Jacobiaan

Jacobiaans voorbeeld

De Jacobiaan en de invertibiliteit van een functie

Relatie van Jacobiaanse matrix met andere bewerkingen

Helling

Hessische matrix

Toepassingen van de Jacobiaanse matrix

Laat een reactie achter Reactie annuleren