Op deze pagina wordt uitgelegd wat een irrationele functie, ook wel radicale functie genoemd, is, evenals alle kenmerken van dit type functie. Je ontdekt ook hoe je het domein van radicale of irrationele functies kunt berekenen en bovendien kun je zien hoe je ze in een grafiek met voorbeelden kunt weergeven en oefenen met oefeningen en problemen die stap voor stap worden opgelost.
Wat is een irrationele (of radicale) functie?
Een irrationele functie betekent hetzelfde als een radicale functie en daarom delen ze een definitie:
Een irrationele functie , ook wel radicale functie genoemd, is een functie met de onafhankelijke variabele x onder het symbool van een wortel.
Zoals we al weten, kan het resultaat van een wortel positief of negatief zijn. De weergave van een irrationele (of radicale) functie heeft dus twee mogelijke curven:
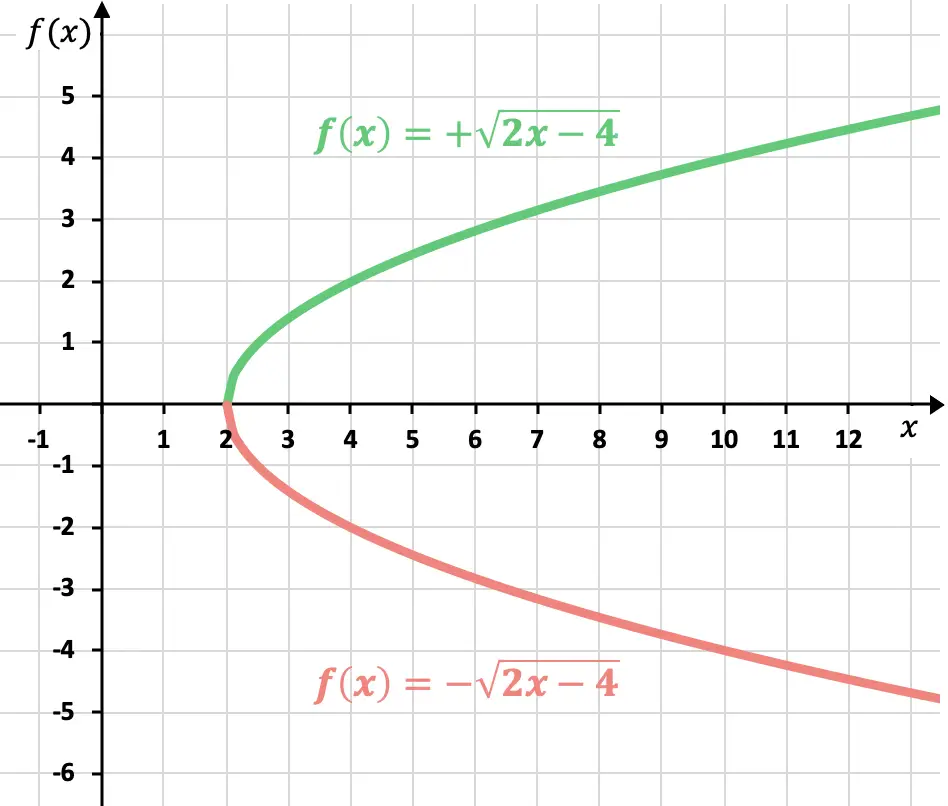
Maar als het teken niet is gespecificeerd, wordt verondersteld dat de positieve functie wordt weergegeven.
Aan de andere kant mag een irrationele functie niet worden verward met een rationele functie. Hoewel ze zeer vergelijkbare namen hebben, zijn het twee totaal verschillende soorten functies.
Domein van een irrationele of radicale functie
Het domein van een functie met wortels hangt af van de pariteit van de wortelindex, dat wil zeggen, het hangt ervan af of de radicale index even of oneven is.
Domein van een functie met wortel of even index
Zoals u wel weet, bestaat er geen wortel (zelfs index) van een negatief getal. Daarom zal een radicale functie met een even index bestaan zolang de inhoud gelijk is aan of groter is dan 0.
Laten we als voorbeeld eens kijken hoe het domein van de volgende radicale of irrationele functie wordt berekend:
![]()
Dit is een radicaal even indexfunctie, dus we moeten kijken wanneer de inhoud positief of nul is :
![]()
We lossen de ongelijkheid op:
![]()
De functie zal dus bestaan wanneer x groter is dan of gelijk is aan 4, en wordt aangegeven door het volgende interval:
![]()
Domein van een functie met wortel van oneven index
Irrationele functies met oneven index hebben dit probleem niet, aangezien de oneven indexwortel van een negatief getal bestaat:
![]()
Daarom bestaan er radicale functies met een oneven index voor elke waarde van x . Of, met andere woorden, het domein bestaat alleen uit reële getallen .
We zullen bijvoorbeeld het definitiedomein berekenen van de volgende radicale functie waarvan de index oneven is:
![]()
Omdat het een irrationele functie is met een oneven index, bestaat het domein uit reële getallen:
![]()
Hoe een irrationele of radicale functie weer te geven
Laten we aan de hand van een voorbeeld kijken hoe we een functie met wortels in een grafiek kunnen weergeven.
- Teken de volgende radicale of irrationele functie in een grafiek:
![]()
Het eerste dat u moet doen, is het domein van de functie vinden. Omdat het een vierkantswortel is, moet alles wat erin staat positief zijn, aangezien er geen vierkantswortel is van een negatief getal. Daarom zal de radicale functie bestaan zolang de inhoud gelijk is aan of groter is dan 0:
![]()
![]()
Het domein van de functie bestaat dus uit alle getallen groter dan of gelijk aan -2. Dat is te zeggen:
![]()
Zodra we het domein van de functie kennen, maken we een tabel met waarden. Het is duidelijk dat hoe meer punten we berekenen, hoe nauwkeuriger de weergave van de functie zal zijn. Maar het berekenen van 3 of 4 punten in het domeininterval is voldoende:
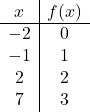
We geven nu de verkregen punten weer in een grafiek :
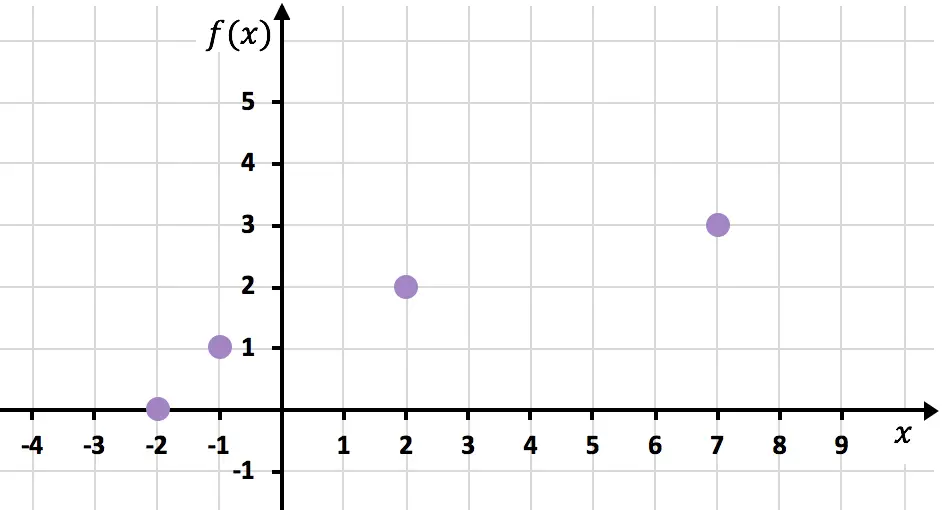
En ten slotte voegen we de punten samen en verlengen we de curve om aan te geven dat de functie blijft groeien:
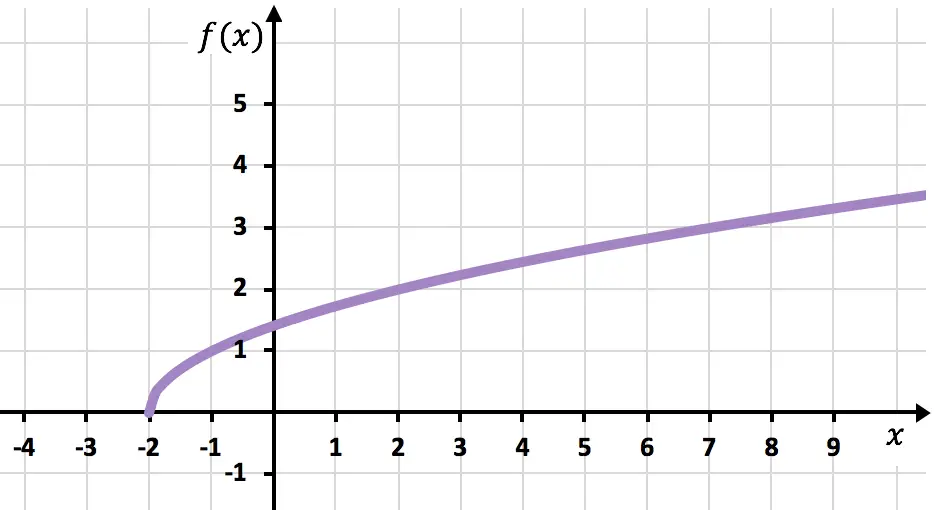
Opgeloste oefeningen over irrationele of radicale functies
Oefening 1
Zoek het domein van de volgende radicale functie:
![]()
De vierkantswortel van een negatief getal bestaat niet. Daarom zal de functie bestaan als het hoofdargument positief of nul is:
![]()
![]()
![]()
![]()
![]()
Oefening 2
Zoek het domein van de volgende irrationele functie:
![]()
De vierkantswortel van een negatief getal heeft geen echte oplossing. Daarom zal de functie bestaan zolang de inhoud van de wortel positief of nul is:
![]()
![]()
![]()
Bedenk dat als we bij een ongelijkheid de zijden van een negatief getal dat vermenigvuldigt of deelt veranderen, we ook het teken van de ongelijkheid moeten roteren.
![]()
![]()
Oefening 3
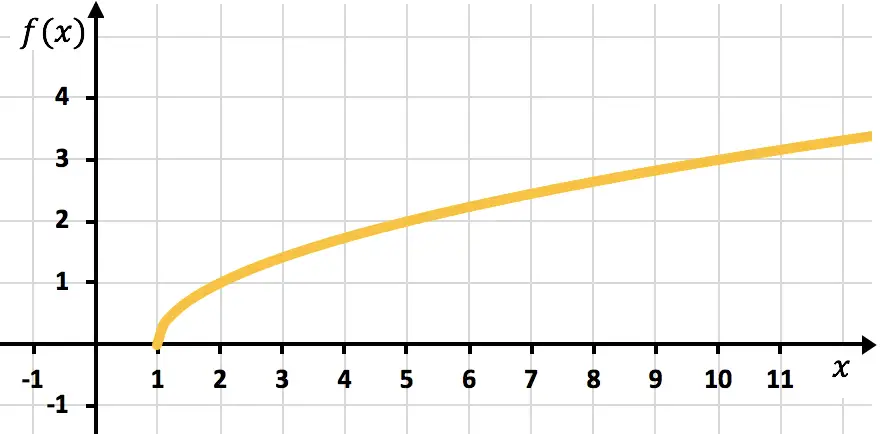
Teken de volgende irrationele functie in een grafiek:
![]()
Allereerst moeten we het domein van de functie berekenen:
![]()
![]()
![]()
Nu creëren we een array van waarden door de waarden van de functie in het domeinbereik te geven:
![]()
![]()
![]()
![]()

Ten slotte plotten we de punten en plotten we de functie in de grafiek:
Oefening 4
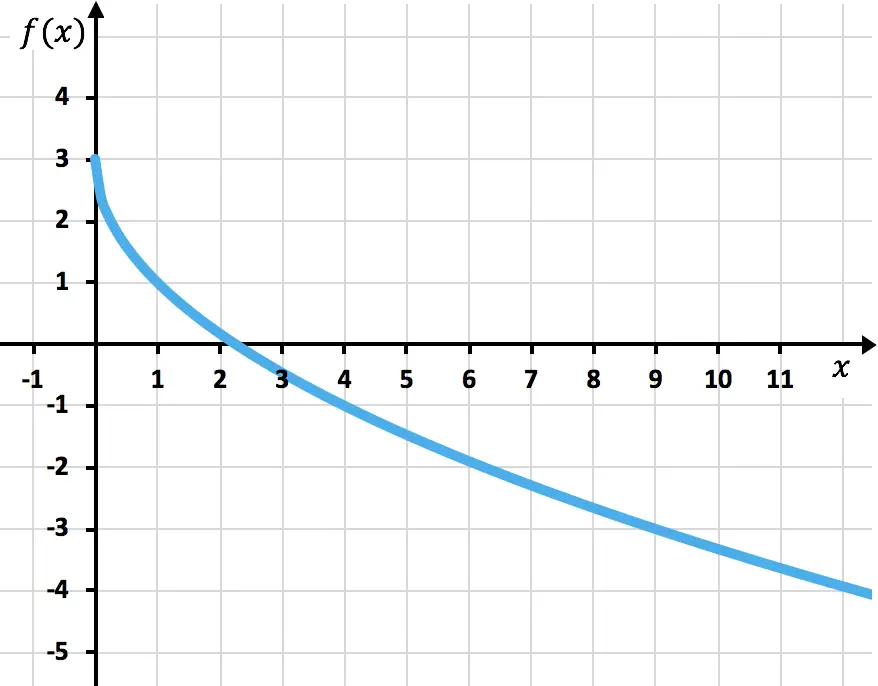
Maak een grafiek van de volgende irrationele of radicaalfunctie:
![]()
Allereerst moeten we het domein van de functie berekenen:
![]()
![]()
Nu creëren we een array van waarden door de waarden van de functie in het domeinbereik te geven:
![]()
![]()
![]()
![]()

Ten slotte plotten we de punten en tekenen we de functie in de grafiek:
Oefening 5
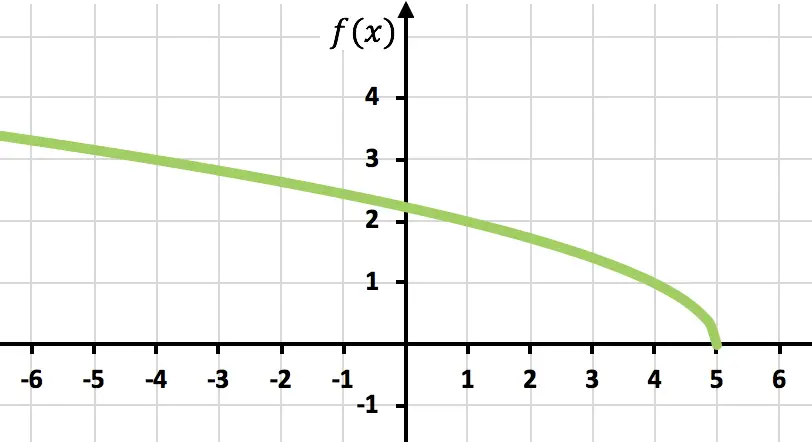
Maak een grafiek van de volgende irrationele of radicaalfunctie:
![]()
Voordat we de functie plotten, moeten we het domein van de functie berekenen:
![]()
![]()
![]()
Bedenk dat als we bij een ongelijkheid de zijden van een negatief getal dat vermenigvuldigt of deelt, veranderen, we ook het teken van de ongelijkheid moeten veranderen.
![]()
![]()
Nu construeren we een tabel met waarden door de functie te evalueren op punten die tot het domein van de functie behoren:
![]()
![]()
![]()
![]()

En tot slot, geef gewoon de punten weer en schilder de functie in de grafiek:
Oefening 6
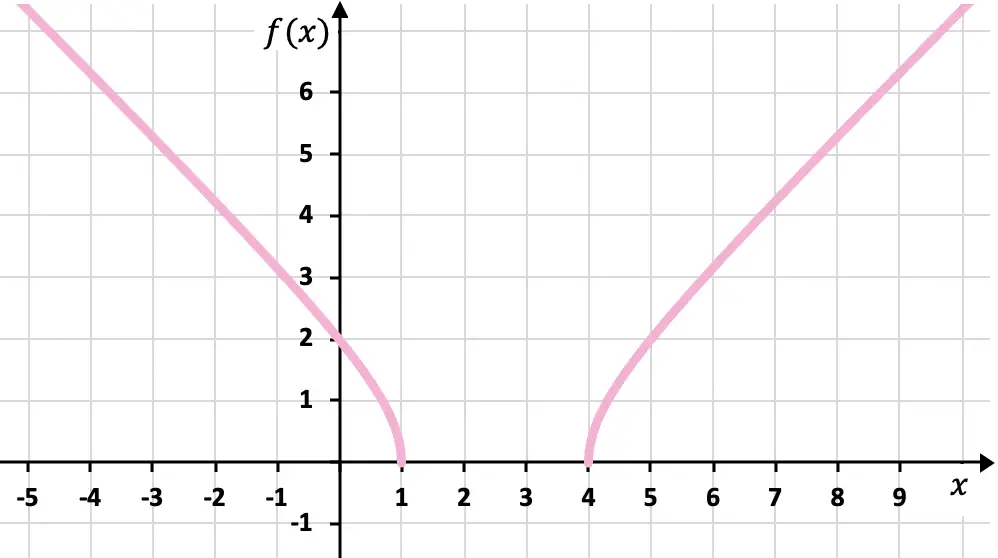
Teken de volgende irrationele of radicale functie in een grafiek:
![]()
We moeten eerst het domein van de functie berekenen:
![]()
In dit geval hebben we een ongelijkheid van de tweede graad verkregen, dus moeten we de formule van de kwadratische vergelijkingen toepassen om deze op te lossen:
![]()
![Rendered by QuickLaTeX.com \displaystyle x=\cfrac{-(-5)\pm \sqrt{(-5)^2-4\cdot 1\cdot 4}}{2\cdot 1} = \cfrac{5\pm 3}{2} =\begin{cases} 4 \\[2ex] 1 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3e5bc09c561e2790b1af96a618a015a0_l3.png)
We verdelen de lijn in drie stukken met de verkregen wortels:

En we vervangen een getal voor elke sectie van de ongelijkheid, om te zien welke secties aan de ongelijkheid voldoen en daarom tot het domein behoren:
![x^2-5x+4\ge 0 \ \xrightarrow{x\ = \ 0} <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://mathority.org/wp-content/ql-cache/quicklatex.com-7c214e08b91825263231bc6eddbbdee1_l3.png" height="54" width="404" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[0^2-5\cdot 0+4\ge 0 \ \longrightarrow \ 4\ge 0 $ ✅$x^2-5x+4\ge 0 \ \xrightarrow{x\ = \ 2}\]" title="Rendered by QuickLaTeX.com"/> 2^2-5\cdot 2+4\ge 0 \ \longrightarrow \ -10\ \cancel{\ge } \ 0″ title=”Rendered by QuickLaTeX.com”></p>
</p>
<p>❌</p>
</p>
<p class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-c9c9c5a39dc152cdcb902dbf0b2e5b59_l3.png)
![]()
![]()
✅
De secties die de ongelijkheid respecteren, zijn dus die van de zijkanten:

Het domein van de functie is daarom:
![]()
Nadat we het domein van de functie hebben berekend, construeren we een waardentabel met de waarden van de functie in het interval van het domein:
![]()
![]()
![]()
![]()
![]()
![]()

Ten slotte vertegenwoordigen we de verkregen punten in de grafiek en plotten we de functie:
Oefening 7
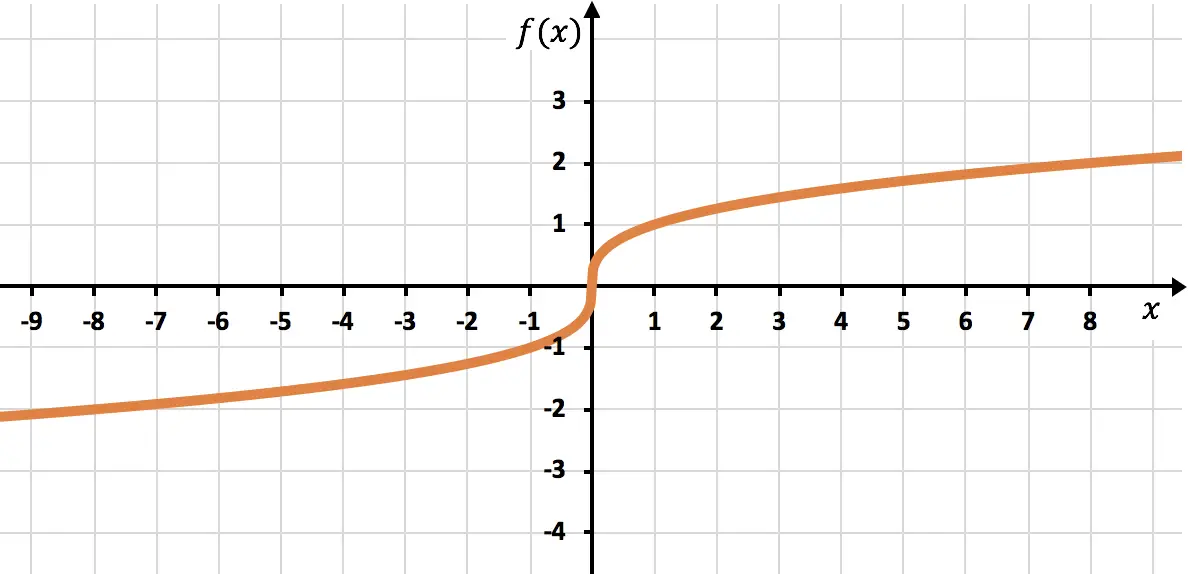
Geef in de grafiek de volgende functie weer, gevormd door een wortel:
![]()
Het is een irrationele functie waarvan de wortel een oneven index heeft, dus het domein van de functie bestaat uit reële getallen:
![]()
We kunnen daarom elk punt gebruiken om de waardentabel te maken. In dit geval zullen we naar veel punten zoeken omdat het een derdemachtswortel is:
![]()
![]()
![]()
![]()
![]()
![]()
![]()

Ten slotte plotten we de gevonden punten en plotten we de functie in de grafiek:
Oefening 8
Los het volgende probleem op dat verband houdt met irrationele (of radicale) functies:
Het verbruik van de batterij van een mobiele telefoon wordt gegeven door de volgende functie:
![]()
Waarbij het verbruik wordt uitgedrukt in milliampère (mA) en
![]()
is de verstreken tijd in minuten.
Bepaal de waarde van de constante
![]()
zodat na 4 minuten het verbruik 35 mA bedraagt.
Dat na 4 minuten het verbruik 35 mA is, betekent dat als t 4 is, f(t) 35 is. Dus f(4)=35.
![]()
![]()
Nu moeten we de vergelijking die we hebben verkregen oplossen. Als je goed kijkt, is het een irrationele vergelijking, omdat het een wortel heeft. Bij dit soort vergelijkingen is het eerste wat je moet doen het isoleren van de wortel van één zijde, die in dit geval al geïsoleerd is. Eenmaal geïsoleerd, moeten we beide zijden van de vergelijking kwadrateren:
![]()
Vervolgens vereenvoudigen we de wortel:
![]()
En we lossen de vergelijking op:
![]()
![]()
![]()
Ten slotte moeten bij irrationele vergelijkingen de oplossingen worden geverifieerd. We moeten daarom K=-1221 in de vergelijking aan het begin vervangen:
![]()
![]()
![]()
![]()
Omdat aan de gelijkheid is voldaan, is K=-1221 een oplossing.