Involutionele matrix

Op deze pagina leer je wat een involuerende matrix is. We laten u ook voorbeelden zien van involutieve matrices met de afmetingen 2×2, 3×3 en 4×4. En ten slotte vind je de formule voor een involutionele matrix.

Wat is een involutionele matrix?

De betekenis van involutionele matrix is als volgt:

Definitie van involutieve matrix : een inverteerbare vierkante matrix waarvan de inverse matrix de matrix zelf is.

$A^{-1} = A$

Goud

$A$

is een willekeurige matrix en

$A^{-1}$

vertegenwoordigt het omgekeerde.

Een involutionele matrix is dus duidelijk een voorbeeld van een reguliere of niet-gedegenereerde matrix .

Als je niet weet wat de inverse van een matrix is, kun je hier zien hoe je de 3×3 inverse matrix berekent. Het is belangrijk om te weten hoe je een matrix moet omkeren, hiervoor moet je echter ook weten hoe de adjoint van een matrix wordt berekend.

Maar terug naar het onderwerp: wanneer een matrix involutief is, geeft de vermenigvuldiging van de matrix met de matrix zelf de identiteitsmatrix. Bekijk de demo:

Elke matrix vermenigvuldigd met zijn inverse geeft de identiteitsmatrix (of eenheidsmatrix). DUS:

$\displaystyle A \cdot A^{-1} = I$

En aangezien het omgekeerde van een involutionele matrix de matrix zelf is:

$\displaystyle A \cdot A = I$

Bijgevolg geeft een kwadratische involutiematrix de identiteitsmatrix:

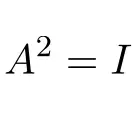
Voorbeelden van involutionele matrices

Voorbeeld van een 2×2 involuerende matrix:

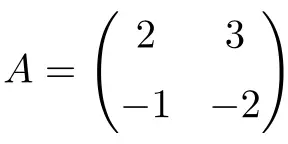
voorbeeld van een involutieve matrix met dimensie 2x2

We kunnen verifiëren dat het een involutionele matrix is door de tweede macht van de matrix te berekenen:

$\displaystyle A^2=\begin{pmatrix} 2 & 3 \\[1.1ex] -1 & -2 \end{pmatrix} \cdot \begin{pmatrix} 2 & 3 \\[1.1ex] -1 & -2 \end{pmatrix}= \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

Omdat matrix A in het kwadraat de identiteitsmatrix is, is matrix A een 2×2 involutionele matrix.

Voorbeeld van een 3×3 involuerende matrix:

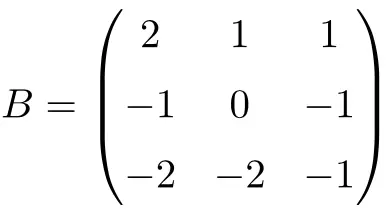
voorbeeld van een involutieve matrix met dimensie 3x3

We kunnen verifiëren dat het een involutionele matrix is door het product van de matrix zelf op te lossen:

$\displaystyle B^2=\begin{pmatrix} 2 & 1 & 1 \\[1.1ex] -1 & 0 & -1 \\[1.1ex] -2 & -2 & -1 \end{pmatrix}\cdot \begin{pmatrix} 2 & 1 & 1 \\[1.1ex] -1 & 0 & -1 \\[1.1ex] -2 & -2 & -1 \end{pmatrix}= \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

Omdat matrix B in het kwadraat de identiteitsmatrix is, is matrix B een 3×3 involutionele matrix.

Voorbeeld van een 4×4 involuerende matrix:

De identiteitsmatrix (of eenheidsmatrix) is, ongeacht de dimensie ervan, per definitie een involutionele matrix.

$\displaystyle I=\begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}$

We kunnen verifiëren dat het een involutionele matrix is door de matrix naar 2 te verhogen:

$\displaystyle I^2=\begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}\cdot \begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}= \begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}$

Omdat de gekwadrateerde identiteitsmatrix de identiteitsmatrix is, is de identiteitsmatrix een 4×4 involutionele matrix.

Het is duidelijk dat de identiteitsmatrix elke dimensie kan hebben, aangezien het eenvoudigweg een diagonale matrix is met alle 1-en op de hoofddiagonaal en de rest 0. De identiteitsmatrix zal dus altijd een involutiematrix zijn, ongeacht de volgorde ervan.

Involuerende matrixformule

Een van de eigenschappen van de involutiematrix is dat de formule ervan bekend kan zijn. Maar het bewijs van de formule voor een involutionele matrix van de tweede orde is behoorlijk vervelend, dus we laten je meteen over aan het resultaat, dat is wat echt belangrijk is. Als je meer geïnteresseerd bent in de demo, kun je deze hieronder stap voor stap in de reacties zien uitgelegd.

De formule voor een involutieve matrix met dimensie 2 × 2 is als volgt:

Daarom zal elke matrix waarvan de belangrijkste diagonale waarden tegengesteld zijn en waarvan de determinant -1 is, een involutionele matrix zijn.

Naast de matrices die door deze formule worden beschreven, moet er echter rekening mee worden gehouden dat de identiteitsmatrix en het tegenovergestelde ervan ook involutionele matrices van orde 2 zijn :

$\displaystyle \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix} \qquad \begin{pmatrix} -1 & 0 \\[1.1ex] 0 & -1 \end{pmatrix}$

Eigenschappen van een involuerende matrix

Involutionele matrices hebben de volgende kenmerken:

De determinant van een involutionele matrix is altijd gelijk aan -1 of +1.

Er bestaat een relatie tussen involutionele matrices en idempotente matrices : de matrix
$A$

is involutioneel als en slechts als de matrix

$\displaystyle Q= \cfrac{1}{2} \cdot (A+I)$

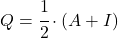
is idempotent.

Ja
$A$

En

$B$

zijn twee pendelende involutionele matrices, dan is het matrixproduct

$AB$

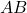
is ook een andere involutionele matrix.

Elke macht van een involutionele matrix resulteert in een andere involutionele matrix. In het bijzonder zal een involutionele matrix die tot een oneven exponent wordt verhoogd, gelijk zijn aan zichzelf, maar als deze wordt verhoogd tot een even exponent zal deze equivalent zijn aan de Identiteitsmatrix.

$A^2 = I$

$A^3 = A$