Impliciete, algemene of cartesiaanse vergelijking van het vlak

Uitleg over hoe de impliciete vlakvergelijking (formule), ook wel de algemene of cartesiaanse vergelijking genoemd, wordt berekend. Bovendien zult u ontdekken hoe u de vergelijking van het vlak kunt vinden op basis van zijn normaalvector. En bovendien kun je stap voor stap voorbeelden en oefeningen zien die opgelost zijn.

Wat is de impliciete of algemene vergelijking van het plan?

In de analytische meetkunde is de impliciete vergelijking van een vlak , ook wel de algemene of cartesiaanse vergelijking van het vlak genoemd, een vergelijking waarmee elk vlak wiskundig kan worden uitgedrukt. Om de impliciete of algemene vergelijking van een vlak te vinden, hebben we een punt en twee lineair onafhankelijke vectoren nodig die bij dat vlak horen.

Formule van de impliciete of algemene vergelijking van het plan

Beschouw een punt en twee richtingsvectoren van een vlak:

$\begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}$

De impliciete, algemene of cartesiaanse vergelijking van een vlak wordt verkregen door de volgende determinant op te lossen en het resultaat gelijk te stellen aan 0:

$\displaystyle \begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} = 0$

De impliciete of algemene vergelijking van het resulterende plan zal dus als volgt zijn:

$Ax+By+Cz+D=0$

Het is belangrijk dat de twee vectoren in de formule lineair onafhankelijk van elkaar zijn, dat wil zeggen dat ze verschillende richtingen moeten hebben. En om aan deze voorwaarde te voldoen is het voldoende dat de twee vectoren niet evenwijdig zijn.

impliciete of algemene of cartesiaanse vergelijking van pan xy in r3

Hoewel het niet nodig is om de reden voor deze formule te weten, kunt u hieronder de demonstratie ervan zien.

Vertrekkend van de parametervergelijkingen van een plan, gaan we verder met de impliciete (of algemene) vergelijking van het plan:

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

Eerst geven we de onafhankelijke term van elke parametervergelijking door naar de andere kant van de vergelijking:

$\displaystyle \begin{cases}x-P_x= \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y-P_y = \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z-P_z = \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

Of gelijkwaardig:

$\displaystyle \begin{cases} \lambda \text{u}_x + \mu \text{v}_x =x-P_x\\[1.7ex] \lambda \text{u}_y + \mu \text{v}_y=y-P_y \\[1.7ex] \lambda\text{u}_z + \mu \text{v}_z =z-P_z\end{cases}$

Wil het bovenstaande stelsel vergelijkingen een haalbare oplossing hebben, dan moet de rangorde van de volgende matrix gelijk zijn aan 2 (stelling van Rouche-Frobenius):

$\displaystyle\begin{pmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z\end{pmatrix}$

Dus als het bereik van de vorige matrix twee moet zijn, moet de 3×3-determinant noodzakelijkerwijs gelijk zijn aan nul:

$\displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0$

En door deze determinant op te lossen, verkrijgen we de algemene, impliciete of cartesiaanse vergelijking van een vlak:

$Ax+By+Cz+D=0$

We hebben dus zojuist de impliciete (of algemene) vergelijking en de parametrische vergelijkingen van het vlak gezien, maar er zijn nog meer manieren om een vlak analytisch uit te drukken, zoals de vectorvergelijking en de canonieke vergelijking. U kunt de formule en uitleg van alle vergelijkingen in het plan bekijken via deze link.

Voorbeeld van hoe u de impliciete of algemene vergelijking van het vlak kunt vinden

Laten we eens kijken hoe we de impliciete (of algemene of cartesiaanse) vergelijking van een vlak kunnen bepalen aan de hand van een voorbeeld:

Zoek de impliciete of algemene vergelijking van het vlak dat door het punt gaat
$P(3,1,-1)$

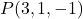
en bevat de vectoren

$\vv{\text{u}}=(2,0,3)$

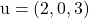
En

$\vv{\text{v}}=(4,-1,2).$

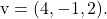
Om de algemene of impliciete vergelijking van het vlak te berekenen, is het noodzakelijk om de volgende determinant op te lossen, gevormd door de twee vectoren, de variabelen en de coördinaten van het punt:

$\displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0$

Dus vervangen we de vectoren en het punt in de formule:

$\displaystyle\begin{vmatrix}2 & 4 & x-3 \\[1.1ex]0 & -1 & y-1 \\[1.1ex]3& 2 & z-(-1) \end{vmatrix} =0$

$\displaystyle\begin{vmatrix}2 & 4 & x-3 \\[1.1ex]0 & -1 & y-1 \\[1.1ex]3& 2 & z+1 \end{vmatrix} =0$

En nu lossen we de determinant van orde 3 op, bijvoorbeeld met de Sarrus-regel of door cofactoren (of plaatsvervangers):

$-2(z+1)+12(y-1)+3(x-3)-4(y-1) = 0$

Nu werken en groeperen we de termen:

$3(x-3)+8(y-1) -2(z+1) = 0$

$3x-9+8y-8 -2z-2 = 0$

$3x+8y-2z-19 = 0$

Daarom is de impliciete of algemene vergelijking van het plan:

$\bm{3x+8y-2z-19 = 0}$

Bereken de impliciete of algemene vergelijking van een vlak op basis van zijn normaalvector

Een heel typisch probleem bij vergelijkingen van een vlak is het vinden van hoe de vergelijking van een bepaald vlak eruit ziet, gegeven een punt en zijn normale (of loodrechte) vector. Laten we dus eens kijken hoe het werkt.

Maar je moet eerst weten dat de componenten X, Y, Z van de vector loodrecht op een vlak respectievelijk samenvallen met de coëfficiënten A, B, C van de impliciete (of algemene) vergelijking van dat vlak.

$\displaystyle \color{orange} \boxed{ \color{black} \quad \pi : \ Ax+By+C+D = 0 \quad \iff \quad \vv{n} = (A,B,C) \quad \vphantom{\Bigl(}}$

Goud

$\vv{n}$

is de vector loodrecht op het vlak

$\pi.$

Zodra we de vorige relatie kennen, laten we een voorbeeld bekijken van het oplossen van dit soort vlakvergelijkingsproblemen:

Bepaal de impliciete of algemene vergelijking van het vlak dat door het punt gaat
$P(1,0,-2)$

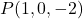
en een van zijn normaalvectoren is

$\vv{n}=(3,-1,2) .$

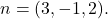
De formule voor de impliciete, algemene of cartesiaanse vergelijking van een vlak is:

$Ax+By+Cz+D=0$

Uit de normaalvector kunnen we dus de coëfficiënten A, B en C vinden, omdat ze equivalent zijn aan de componenten van zijn normaalvector:

$\vv{n}=(3,-1,2) \ \longrightarrow \ 3x-1y+2z+D=0$

Hoewel we alleen de parameter D hoeven te vinden. Om dit te doen, vervangen we de coördinaten van het punt dat bij het vlak hoort in de vergelijking:

$P(1,0,-2)$

$3\cdot 1-0+2\cdot (-2)+D=0$

$3-4+D=0$

$-1+D=0$

$D=1$

De impliciete of algemene vergelijking van het plan is dus:

$\bm{3x-y+2z+1 = 0}$

Opgeloste problemen van de impliciete of algemene vergelijking van het vlak

Oefening 1

Zoek de impliciete of algemene vergelijking van het vlak dat door het punt gaat

$P(-2,1,3)$

en bevat de vectoren

$\vv{\text{u}}=(4,1,3)$

$\vv{\text{v}}=(5,3,-1).$

zie oplossing

Om de algemene of impliciete vergelijking van het vlak te berekenen, is het noodzakelijk om de volgende determinant op te lossen, gevormd door de twee vectoren, de drie variabelen en de coördinaten van het punt:

$\displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0$

Dus vervangen we de vectoren en het punt in de formule:

$\displaystyle\begin{vmatrix}4 & 5 & x+2 \\[1.1ex]1 & 3 & y-1 \\[1.1ex]3& 1 & z+1 \end{vmatrix} =0$

En nu lossen we de determinant van de 3×3 matrix op met de methode van jouw keuze:

$12(z+1)+15(y-1)+1(x+2)-9(x+2)-4(y-1)-5(z+1) = 0$

Ten slotte voeren we de bewerkingen uit en groeperen we vergelijkbare termen:

$-8(x+2)+11(y-1)+7(z+1) = 0$

$-8x-16+11y-11+7z+7=0$

$-8x+11y+7z-20= 0$

De impliciete of algemene vergelijking van het plan is dus:

$\bm{-8x+11y+7z-20 = 0}$

Oefening 2

Bepaal of het punt is

$P(-1,5,-3)$

behoort tot het volgende plan:

$\pi : \ 2x+y+6z-5=0$

zie oplossing

Om het punt in het vlak te laten liggen, moet de vergelijking ervan worden geverifieerd. Daarom moeten we de cartesiaanse coördinaten van het punt in de vergelijking van het vlak vervangen en controleren of aan de vergelijking is voldaan:

$2x+y+6z-5=0$

$P(-1,5,-3)$

$2\cdot (-1)+5+6\cdot (-3)-5=0$

$-2+5-18-5=0$

$-20\neq 0$

Het punt respecteert de vergelijking van het vlak niet en maakt dus geen deel uit van dit vlak.

Oefening 3

Zoek de impliciete (of algemene) vergelijking van het plan die de volgende drie punten bevat:

$A(5,-1,-2) \qquad B(2,1,3) \qquad C(4,1,-2)$

zie oplossing

Om de impliciete vergelijking van het vlak te vinden, moeten we twee lineair onafhankelijke vectoren vinden die in het vlak binden. En hiervoor kunnen we twee vectoren berekenen die worden gedefinieerd door de 3 punten:

$\vv{AB} = B - A = (2,1,3) - (5,-1,-2) = (-3,2,5)$

$\vv{AC} = C - A = (4,1,-2) - (5,-1,-2) = (-1,2,0)$

De coördinaten van de twee gevonden vectoren zijn niet proportioneel, dus zijn ze feitelijk lineair onafhankelijk van elkaar.

Nu kennen we al twee richtingsvectoren en één punt van het vlak, dus we kunnen de formule voor de algemene vergelijking van het vlak al toepassen:

$\displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0$

We vervangen de vectoren en een van de drie punten in de formule:

$\displaystyle\begin{vmatrix}-3 & -1 & x-5 \\[1.1ex]2 & 2 & y+1 \\[1.1ex]5& 0 & z+2 \end{vmatrix} =0$

En ten slotte lossen we de determinant op:

$-6(z+2)-5(y+1)-10(x-5)+2(z+2)=0$

$-10(x-5)-5(y+1)-4(z+2)=0$

$-10x+50-5y-5-4z-8=0$

$-10x-5y-4z+37=0$

Kortom, de impliciete, algemene of cartesiaanse vergelijking van het betreffende vlak is:

$\bm{-10x-5y-4z+37=0}$

Oefening 4

Berekent de impliciete of algemene vergelijking van het vlak in de ruimte dat door het punt gaat

$P(3,4,-3)$

en een van zijn normaalvectoren is

$\vv{n}=(5,-2,-3) .$

zie oplossing

De formule voor de impliciete, algemene of cartesiaanse vergelijking van een vlak is:

$Ax+By+Cz+D=0$

Welnu, uit de normaalvector kunnen we de coëfficiënten A, B en C vinden, omdat ze respectievelijk gelijk zijn aan de componenten van de normaalvector:

$\vv{n}=(5,-2,-3) \ \longrightarrow \ 5x-2y-3z+D=0$