Hier vind je wat de identiteitsfunctie is. Bovendien kunt u zien hoe u de identiteitsfunctie grafisch kunt weergeven en wat de kenmerken ervan zijn.
Wat is een identiteitsfunctie?
Een identiteitsfunctie is die functie die als afbeelding dezelfde waarde heeft als het argument. De identiteitsfunctie kan worden uitgedrukt met de term id .
Daarom is de wiskundige uitdrukking voor de identiteitsfunctie:
![]()
Het beeld van de identiteitsfunctie voor x=1 is bijvoorbeeld 1 waard, het beeld van x=2 is 2 waard, het beeld van x=3 is 3 waard,…
![Rendered by QuickLaTeX.com \begin{array}{c}f(1)=1\\[2ex]f(2)=2\\[2ex]f(3)=3\\ \bm{\vdots}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4b85e48e3f36d1eb4271b265aaf35bef_l3.png)
De identiteitsfunctie is een voorbeeld van een lineaire functie. In de volgende link kunt u meer voorbeelden van dit soort functies zien:
➤ Zie: voorbeelden van lineaire functies
Grafische weergave van de identiteitsfunctie
De grafiek van de identiteitsfunctie komt overeen met een lijn die de bissectrice is van het eerste en derde kwadrant.
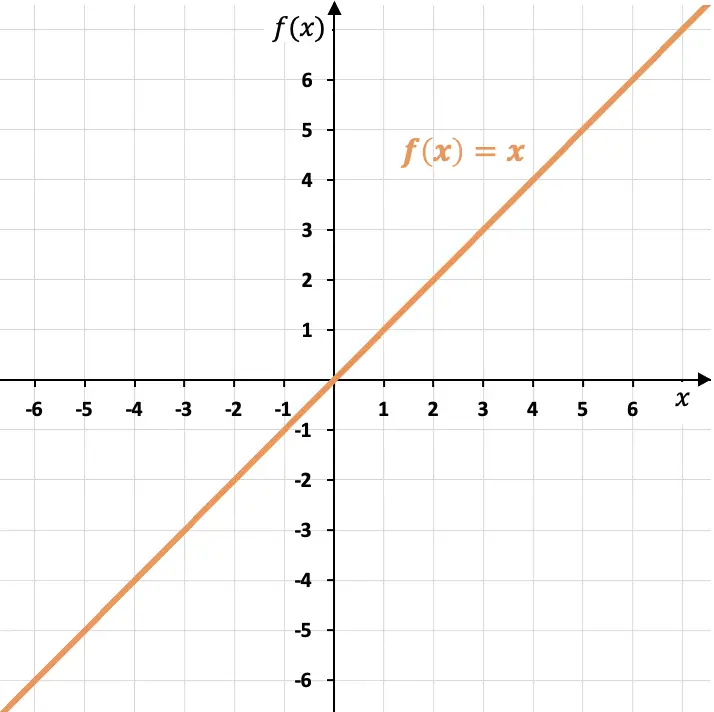
Zoals u kunt zien, gaat de identiteitsfunctie door de oorsprong van de coördinaten (punt (0,0)) en heeft een helling gelijk aan eenheid (m=1), aangezien één eenheid van de variabele toeneemt en voor elke waarde van de onafhankelijke variabele X. Bovendien vormt de identiteitsfunctie een hoek van 45º met de X-as.
Kenmerken van de identiteitsfunctie
De identiteitsfunctie heeft de volgende eigenschappen:
- Het domein van de identiteitsfunctie bestaat uit alle reële getallen:
![]()
- Het bereik (of bereik) van de identiteitsfunctie bestaat ook uit alle reële getallen:
![]()
- De identiteitsfunctie is een continue en bijectieve functie.
- Bovendien bestaat de identiteitsfunctie uit een oneven functie, wat betekent dat het een symmetrische functie is ten opzichte van de oorsprong van de coördinaten.
![]()
➤ Zie: oneven symmetrische functie
- De identiteitsfunctie neemt over het hele domein toe en de helling is gelijk aan 1.
![]()
- Snijdt de x-as (OX-as) en de y-as (Y-as) op hetzelfde punt: de coördinaatoorsprong.
![]()
- Het kan worden geclassificeerd als een polynomiale functie van de eerste graad.
- De identiteitsfunctie fungeert als een neutraal element van de functiesamenstelling . Zodat elke functie die met de identiteitsfunctie is samengesteld, resulteert in de functie zelf.
![]()
- De waarde
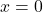
is de enige wortel van dit type functie.
- De limiet van de identiteitsfunctie wanneer x neigt naar plus oneindig of minus oneindig geeft respectievelijk plus oneindig en minus oneindig:
![]()
![]()
- De identiteitsfunctie heeft dus geen asymptoot.
- De afgeleide van de identiteitsfunctie is de constante functie met waarde 1:
![]()
- De integraal van de identiteitsfunctie is de kwadratische functie:
![]()