Opmerkelijke identiteiten (of opmerkelijke producten) -

Hier vindt u de uitleg over de resolutie van alle soorten opmerkelijke identiteiten (of opmerkelijke producten). Je zult kunnen zien wat de formules van alle opmerkelijke identiteiten zijn, evenals voorbeelden en oefeningen die stap voor stap worden opgelost. Daarnaast laten we u zien waarvoor deze beroemde wiskundige regels worden gebruikt.

👉👉 Hieronder leggen we elke opvallende identiteit stap voor stap uit, maar als je wilt, kun je direct naar de tabel 😉 gaan waar alle formules zijn samengevat . 👈👈

Wat zijn opmerkelijke identiteiten (of opmerkelijke producten)?

Opmerkelijke identiteiten , ook wel opmerkelijke producten of opmerkelijke gelijkheden genoemd, zijn wiskundige regels waarmee bewerkingen met polynomen direct kunnen worden opgelost.

De meest voorkomende opmerkelijke identiteitsformules zijn het kwadraat van een som , het kwadraat van een verschil (of aftrekking) en de som maal het verschil .

opmerkelijke productidentiteiten of gelijkheden

Maar hieronder leren we je niet alleen hoe je deze opmerkelijke producten kunt berekenen, maar laten we je ook alle soorten opmerkelijke identiteiten zien die er bestaan.

Opmerkelijke identiteitsformules (of producten)

Zodra we de definitie van opmerkelijke producten (of opmerkelijke gelijkheden) hebben gezien, zullen we zien wat de formules voor opmerkelijke identiteiten zijn. Aan de andere kant, als u geïnteresseerd bent in formuledemo’s, kunt u deze formule bekijken door op de knoppen “demo bekijken” te klikken.

kwadraat van een som

Het kwadraat van een som , of som kwadraat , is een van de belangrijkste opmerkelijke identiteiten. Preciezer gezegd, het is een binomiaal met twee positieve termen tot de macht 2, dat wil zeggen dat de algebraïsche uitdrukking (a+b) ² is.

De formule voor het kwadraat van een som is dus:

opmerkelijke identiteiten in het kwadraat van een som

Zie de formuledemonstratie

Als we uitgaan van een positieve binomiaal verhoogd naar 2:

$(a+b)^2$

Wiskundig gezien is het bovenstaande kwadraat gelijk aan de factor

$(a+b)$

vermenigvuldigd met zichzelf:

$(a+b)^2=(a+b)\cdot (a+b)$

We vermenigvuldigen dus polynomen met behulp van de distributieve eigenschap:

$\begin{aligned} (a+b)\cdot (a+b) & = a\cdot a +a\cdot b +b\cdot a +b\cdot b \\[2ex] &=a^2+ab+ba+b^2 \end{aligned}$

Van de vier verkregen termen,

$ab$

$ba$

lijken op elkaar, zodat we ze kunnen groeperen:

$a^2+ab+ba+b^2 = a^2+2ab+b^2$

Zozeer zelfs dat we al zijn aangekomen bij de uitdrukking van de formule voor een kwadratische som, waarvoor deze is afgeleid:

$(a+b)^2= a^2+2ab+b^2$

Uit curiositeit wordt de ontwikkeling van de expressie voor dit soort opmerkelijke producten een perfecte vierkante trinominaal genoemd.

Zodat het kwadraat van een som gelijk is aan het kwadraat van de eerste term, plus tweemaal het product van de eerste door de tweede, plus het kwadraat van de tweede.

Om een kwadratische som op te lossen is het dus niet voldoende om elke optelling van beide te verhogen, maar bovendien moeten de twee optellingen met elkaar en met 2 worden vermenigvuldigd. Het is belangrijk om dit te onthouden omdat dit een zeer typische fout van dit type is. van product Het is opmerkelijk om deze term te vergeten.

opmerkelijke polynomiale en binominale identiteiten

Voorbeeld:

Bereken de volgende opmerkelijke identiteit door de overeenkomstige formule toe te passen:

$(x+5)^2$

Zoals we zojuist hebben gezien, is de formule voor de opmerkelijke gelijkheid van een kwadraatsom:

$(a+b)^2=a^2+2ab+b^2$

Daarom moeten we eerst de parameters identificeren

$a$

$b$

van de formule. In dit geval,

$a$

vertegenwoordigt de

$x$

van het paar en

$b$

komt overeen met nummer 5:

$\left. \begin{array}{l} (a+b)^2\\[2ex] (x+5)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=5 \end{array}$

Dus nu we de waarden kennen van

$a$

en van

$b,$

we kunnen de formule voor een kwadraat van een positieve binomiaal gebruiken om het resultaat te vinden:

voorbeelden van opmerkelijke vierkante identiteiten

kwadraat van een verschil

Het kwadraat van een verschil , of het kwadraat van het verschil , is een van de drie meest gebruikte opmerkelijke identiteiten. In het bijzonder komt het overeen met een binomiale term die wordt gevormd door een positieve term en een andere negatieve term verhoogd tot 2, dat wil zeggen dat de algebraïsche uitdrukking ervan (ab) ² is.

De formule voor het kwadraat van een verschil (of het kwadraat van een aftrekking) is dus als volgt:

Bekijk de formuledemo

Uit de binomiale uitdrukking van een kwadratische aftrekking:

$(a-b)^2$

Het is duidelijk dat de vorige macht gelijk is aan het product van de factor

$(a-b)$

vermenigvuldigd met zichzelf:

$(a-b)^2= (a-b)\cdot (a-b)$

Nu vermenigvuldigen we de twee haakjes door de distributieve eigenschap toe te passen:

$\begin{aligned}(a-b)\cdot (a-b) & = a\cdot a +a\cdot (-b) - b\cdot a - b \cdot (-b) \\[2ex] & = a^2-ab-ba+b^2 \end{aligned}$

U hoeft dus alleen maar vergelijkbare termen te groeperen om de controle van de formule te voltooien:

$a^2-ab-ba+b^2 = a^2-2ab +b^2$

Vervolgens wordt de formule voor het kwadraat van een verschil wiskundig bewezen:

$(a-b)^2=a^2-2ab+b^2$

Zodat het kwadraat van een verschil gelijk is aan het kwadraat van de eerste term, minus tweemaal het product van de eerste en de tweede, plus het kwadraat van de tweede.

Wat betreft de opmerkelijke gelijkheid van de som in het kwadraat, mogen we niet vergeten de middelste term van de formule te gebruiken, aangezien de volgende vergelijking onjuist is:

veelvoorkomende opmerkelijke identiteitsfouten

Voorbeeld:

Los de volgende opmerkelijke gelijkheid van een kwadraatverschil op:

$(x-3)^2$

Het is het opmerkelijke product van een kwadratische aftrekking, daarom is het noodzakelijk om de overeenkomstige formule toe te passen:

$(a-b)^2=a^2-2ab+b^2$

Vervolgens moeten we identificeren wat de waarden van de onbekenden zijn.

$a$

$b$

van de formule. In dit geval,

$a$

is de variabele

$x$

$b$

komt overeen met nummer 3:

$\left. \begin{array}{l} (a-b)^2\\[2ex] (x-3)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=3 \end{array}$

Houd er rekening mee dat het minteken geen deel uitmaakt van de parameter

$b,$

maar u moet altijd het getal zonder teken nemen om deze formule correct toe te passen.

We kennen de waarden dus al van

$a$

en van

$b$

, is het daarom voldoende om deze waarden in de formule te vervangen om de opmerkelijke identiteit op te lossen:

voorbeelden en oefeningen die stap voor stap worden opgelost van opmerkelijke gelijkheden

som per verschil

Het product van een som en een verschil is een van de 3 meest gebruikte opmerkelijke identiteiten. Zoals de naam doet vermoeden, is het een positieve binominale vermenigvuldiging met zijn geconjugeerde binominale waarde (dezelfde binomiale maar met een gewijzigd tussenteken), dat wil zeggen dat de algebraïsche uitdrukking van dit type opmerkelijk product (a +b) · (ab) is. .

De formule voor de opmerkelijke identiteit van het product van een som door een verschil is als volgt:

identiteiten, producten en opmerkelijke gelijkheden van middelbare scholen 2, 3 en 4 die

Zie de formuledemonstratie

Beginnend met het product van een som door twee willekeurige termen af te trekken:

$(a+b)\cdot (a-b)$

Om de formule aan te tonen, hoeven we alleen maar het eerste haakje te vermenigvuldigen met het tweede haakje met behulp van de distributieve eigenschap:

$\begin{array}{l}(a+b)\cdot (a-b)= \\[2ex] = a\cdot a +a\cdot (-b) +b \cdot a +b\cdot (-b) =\\[2ex] = a^2 -ab+ba-b^2\end{array}$

Nu groeperen we soortgelijke termen samen:

$a^2 -ab+ba-b^2=a^2-b^2$

En zo hebben we de uitdrukking van opmerkelijke gelijkheid bereikt. Zo wordt de formule voor dit opmerkelijke type identiteit gedemonstreerd:

$(a+b)\cdot (a-b) =a^2-b^2$

Het product van de som door het verschil van twee grootheden is dus gelijk aan het verschil van de kwadraten van deze grootheden. Of met andere woorden: het vermenigvuldigen van de som van twee verschillende termen door diezelfde twee termen van elkaar af te trekken, komt neer op het kwadrateren van elk van de twee termen en ze aftrekken.

Voorbeeld:

Vind, met behulp van de overeenkomstige formule, het volgende opmerkelijke product van de som door het verschil van twee verschillende termen:

$(x+2)\cdot (x-2)$

Zoals we hierboven hebben gezien, is de formule voor de opmerkelijke gelijkheid van een som vermenigvuldigd met een verschil als volgt:

$(a+b)\cdot (a-b) =a^2-b^2$

Allereerst moeten we de waarden van de letters identificeren

$a$

$b$

van de formule. In dit geval

$a$

corresponderen met de variabele

$x$

$b$

komt overeen met nummer 2.

$\left. \begin{array}{l} (a+b)\cdot (a-b) \\[2ex] (x+2)\cdot (x-2) \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=2 \end{array}$

En als we al weten welke waarden de parameters aannemen

$a$

$b,$

We passen de formule toe voor het product van de som door het verschil:

kwadraat van een trinominaal

Het kwadraat van een trinominaal (veelterm gevormd uit 3 termen) is gelijk aan het kwadraat van de eerste term, plus het kwadraat van de tweede term, plus het kwadraat van de derde term, plus tweemaal de eerste bij de tweede, plus tweemaal de eerste bij de derde, plus tweemaal de tweede voor de derde.

Wat zijn de formules voor alle opmerkelijke identiteiten, producten of gelijkheden?

Bekijk de formuledemo

Van elk trinominaal kwadraat:

$(a+b+c)^2$

Het bovenstaande vierkant kan worden verwerkt in de trinominaal, vermenigvuldigd met zichzelf:

$(a+b+c)^2 = (a+b+c)(a+b+c)$

Nu lossen we de polynomiale vermenigvuldiging op:

$(a+b+c)(a+b+c)= a^2+ab+ac+ba+b^2+bc+ca+cb+c^2$

En ten slotte groeperen we soortgelijke termen:

$a^2+ab+ac+ba+b^2+bc+ca+cb+c^2 = a^2+b^2+c^2+2ab+2ac+2bc$

Op deze manier zijn we al aangekomen bij de uitdrukking van de formule, dus de formule voor het kwadraat van een trinominaal wordt gedemonstreerd:

$(a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc$

Voorbeeld:

Zoek de volgende opmerkelijke gelijkheid:

$\left(x^2+x+3\right)^2$

De formule voor het kwadraat van een trinominaal is:

$(a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc$

Zoals bij alle opmerkelijke gelijkheden moet je eerst de waarden van de onbekenden in de formule identificeren. Bij deze oefening

$a$

Oosten

$x^2,$

de coëfficiënt

$b$

overeenkomen met de

$x,$

$c$

is de onafhankelijke term 3:

$\left. \begin{array}{c} (a+b+c)^2\\[2ex] \left(x^2+x+3\right)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x^2 \\[2ex] b=x \\[2ex] c=3 \end{array}$

En als we de waarden al kennen, vervangt u deze waarden eenvoudigweg in de formule en voert u de berekeningen uit:

rekenmachine van opmerkelijke identiteiten, producten en gelijkheden

Opmerkelijke identiteiten (of producten) in blokjes

We hebben zojuist alle opmerkelijke identiteiten in het kwadraat bestudeerd, dat wil zeggen alle soorten opmerkelijke identiteiten die worden gevormd door machten verhoogd tot 2. Nu gaan we opmerkelijke identiteiten analyseren in de derde macht. Natuurlijk zijn gekubeerde identiteitsformules iets ingewikkelder, maar ze zijn ook erg handig.

kubus van een som

Het opmerkelijke kubusproduct van een som is een binomiaal (polynoom met slechts twee monomialen) tot de macht 3 waarvan de twee elementen positief zijn. Daarom wordt de derde macht van een som algebraïsch uitgedrukt als (a+b) ³ .

De formule voor de opmerkelijke gelijkheid van de derde macht van een som is:

Wat zijn alle opmerkelijke producten, identiteiten of banden?

Zie de formuledemonstratie

Uitgaande van een positieve binominale kubus:

$(a+b)^3$

De bovenstaande macht kan worden verwerkt in het product van de factor

$(a+b)$

door zijn vierkant:

$(a+b)^3=(a+b)\cdot (a+b)^2$

Op dezelfde manier, zoals we zagen bij opmerkelijke kwadratische gelijkheden, de binomiaal

$(a+b)$

Het kan worden opgelost met de formule voor het kwadraat van een som:

$(a+b)\cdot (a+b)^2=(a+b)\cdot (a^2+2ab+b^2)$

Vervolgens vermenigvuldigen we de twee polynomen met elkaar:

$\begin{aligned} (a+b)\cdot (a^2+2ab+b^2) & = a\cdot a^2 +a\cdot 2ab + a\cdot b^2+b\cdot a^2 +b\cdot 2ab +b \cdot b^2 \\[2ex] & = a^3+2a^2b+ab^2+ba^2+2ab^2+b^3 \end{aligned}$

Ten slotte hoeven we alleen maar vergelijkbare termen te groeperen:

$a^3+2a^2b+ab^2+ba^2+2ab^2+b^3 = a^3+3a^2b+3ab^2+b^3$

En zo wordt de formule voor de opmerkelijke identiteit van een binominale som in de derde macht geverifieerd:

$(a+b)^3 = a^3+3a^2b+3ab^2 +b^3$

Kortom, een som verhoogd tot 3 is gelijk aan de derde macht van de eerste, plus drie keer het kwadraat van de eerste bij de tweede, plus drie keer de eerste bij het kwadraat van de tweede, plus de derde macht van de tweede.

Voorbeeld:

Los de volgende opmerkelijke identiteit van een gekubeerde som op met behulp van de overeenkomstige formule:

$(x+2)^3$

In dit probleem hebben we een binomiaal tot de macht 3 waarvan de twee termen positief zijn. We moeten daarom de formule voor een kubusvormige som gebruiken:

$(a+b)^3 = a^3+3a^2b+3ab^2 +b^3$

We moeten nu de waarde van de parameters vinden

$a$

$b$

van de formule. In dit geval,

$a$

corresponderen met de variabele

$x$

$b$

staat op nummer 2.

$\left. \begin{array}{l} (a+b)^3\\[2ex] (x+2)^3 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=2 \end{array}$

Waarmee we het opmerkelijke product berekenen door de waarden van te vervangen

$a$

en van

$b$

in de formule:

10 voorbeelden van opmerkelijke producten of identiteiten

kubus van een verschil

De kubus van een verschil , of de kubus van een aftrekking , is een binomiaal tot de macht 3 met een term met een negatief teken. De wiskundige uitdrukking voor dit opmerkelijke producttype is dus (ab) ³ .

De formule voor de derde macht van een verschil (of aftrekking) is:

opmerkelijke kubieke identiteiten, producten of gelijkheden

Zie de formuledemonstratie

Het is duidelijk dat het bewijs van deze formule sterk lijkt op dat van het opmerkelijke product van een som in blokjes. Maar in dit geval gaan we uit van een negatief derdegraads binomiaal:

$(a-b)^3$

Het is duidelijk dat de eerdere potentiëring kan worden ontleed in het product van de factor

$(a-b)$

vermenigvuldigd met het kwadraat:

$(a-b)^3=(a-b)\cdot (a-b)^2$

Dus, zoals we bestudeerden in opmerkelijke kwadratische identiteiten, de binomiale

$(a-b)$

Het kan worden berekend met de formule voor het kwadraat van een verschil:

$(a-b)\cdot (a-b)^2=(a-b)\cdot (a^2-2ab+b^2)$

We produceren nu het product van de twee polynomen:

$\begin{aligned} (a-b)\cdot (a^2-2ab+b^2) & = a\cdot a^2 +a\cdot (-2ab) + a\cdot b^2-b\cdot a^2 -b\cdot (-2ab)-b \cdot b^2 \\[2ex] & = a^3-2a^2b+ab^2-ba^2+2ab^2-b^3 \end{aligned}$

En de laatste stap is het groeperen van vergelijkbare termen:

$a^3-2a^2b+ab^2-ba^2+2ab^2-b^3 = a^3-3a^2b+3ab^2-b^3$

Zo wordt de formule voor de opmerkelijke identiteit van een afgetrokken binomiaal verheven tot de kubus geverifieerd:

$(a-b)^3 = a^3-3a^2b+3ab^2-b^3$

Dus een verschil (of aftrekking) verhoogd tot drie is gelijk aan de derde macht van de eerste, minus drie keer het kwadraat van de eerste door de tweede, plus drie keer de eerste door het kwadraat van de tweede, minus de derde macht van de tweede.

Voorbeeld:

Bereken de volgende gekubeerde binomiaal (verschil) met behulp van de bijbehorende formule:

$(3x-2)^3$

In deze oefening hebben we een paar met een positief element en een negatief element. We moeten daarom de formule voor een kubusvormig verschil gebruiken:

$(a-b)^3 = a^3-3a^2b+3ab^2 -b^3$

Eerst identificeren we, zoals altijd, de waarde van de onbekenden

$a$

$b$

van de formule. In dit geval

$a$

vertegenwoordigt het monomiaal

$3x$

$b$

is de onafhankelijke term van de binominale term, dat wil zeggen 2.

$\left. \begin{array}{l} (a-b)^3\\[2ex] (3x-2)^3 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=3x \\[2ex] b=2 \end{array}$

Houd er rekening mee dat de parameter

$b$

is eenvoudigweg gelijk aan 2, zonder het negatieve teken van het getal. Het is belangrijk om dit in gedachten te houden om de formule goed toe te passen.

Ten slotte vinden we de opmerkelijke identiteit door de waarden van

$a$

en van

$b$

in de formule:

opmerkelijke identiteiten, producten en gelijkheden ontwikkelen

Overzichtstabel van opmerkelijke identiteiten

Samenvattend hebben we een tabel gemaakt met alle opmerkelijke identiteiten (of producten) die we hebben gezien, zodat u ze gemakkelijker kunt bestuderen. 😉

formules van identiteiten of gelijkheden van opmerkelijke producten

Opgeloste oefeningen van opmerkelijke identiteiten (of producten)

Om ervoor te zorgen dat je het begrip van opmerkelijke identiteiten, ook wel opmerkelijke producten of opmerkelijke gelijkheden genoemd, begrijpt, hebben we verschillende oefeningen voorbereid die stap voor stap worden opgelost. Je kunt ze proberen uit te voeren en dan controleren of je het goed hebt gedaan met de oplossingen van de oefeningen.

⬇⬇ Vergeet niet dat je ons hieronder in de reacties al je vragen kunt stellen! ⬇⬇

Oefening 1

Vouw de volgende opmerkelijke identiteiten uit (somkwadraten):

$\text{A)} \ (x+3)^2$

$\text{B)} \ (6x+2)^2$

$\text{C)} \ \left(x^2+7\right)^2$

$\text{D)} \ (5x+8y)^2$

zie oplossing

Alle opmerkelijke identiteiten in het probleem zijn gekwadrateerde sommen, dus in dit geval moeten we altijd dezelfde formule toepassen:

$(a+b)^2=a^2+2ab+b^2$

$\text{A)} \ \begin{aligned}(x+3)^2& =x^2+2\cdot x\cdot 3 +3^2\\[2ex] & = \bm{x^2+6x +9}\end{aligned}$

$\text{B)} \ \begin{aligned}(6x+2)^2 & =(6x)^2+2\cdot 6x \cdot 2+2^2\\[2ex] & = \bm{36x^2+24x+4}\end{aligned}$

$\text{C)} \ \begin{aligned}\left(x^2+7\right)^2 & = \left(x^2\right)^2+2\cdot x^2\cdot 7 +7^2\\[2ex] & = \bm{x^4+14x^2 +49}\end{aligned}$

$\text{D)} \ \begin{aligned}(5x+8y)^2 & =(5x)^2+2\cdot 5x\cdot 8y +(8y)^2\\[2ex] & = \bm{25x^2+80xy+64y^2}\end{aligned}$

Oefening 2

Ontwikkel de volgende opmerkelijke producten (verschillen in het kwadraat):

$\text{A)} \ (x-2)^2$

$\text{B)} \ (3-7x)^2$

$\text{C)} \ \left(x^2-6\right)^2$

$\text{D)} \ (-3x+y)^2$

zie oplossing

Alle opmerkelijke producten in deze oefening zijn kwadratische aftrekkingen, dus we hoeven maar één formule toe te passen:

$(a-b)^2=a^2-2ab+b^2$

$\text{A)} \ \begin{aligned}(x-2)^2& =x^2-2\cdot x\cdot 2 +2^2\\[2ex] & = \bm{x^2-4x +4}\end{aligned}$

$\text{B)} \ \begin{aligned}(3-7x)^2 & =3^2-2\cdot 3\cdot 7x +(7x)^2\\[2ex] & = \bm{9-42x+49x^2}\end{aligned}$

$\text{C)} \ \begin{aligned}\left(x^2-6\right)^2 & = \left(x^2\right)^2-2\cdot x^2\cdot 6 +6^2\\[2ex] & = \bm{x^4-12x^2 +36}\end{aligned}$

$\text{D)} \ \begin{aligned}(-3x+y)^2 & = (y-3x)^2 \\[2ex] & = y^2-2\cdot y\cdot 3x +(3x)^2\\[2ex] & = \bm{y^2-6yx+9x^2}\end{aligned}$

Oefening 3

Ontwikkel de volgende opmerkelijke gelijkheden (producten van sommen door verschillen):

$\text{A)} \ (x+5)(x-5)$

$\text{B)} \ (2x+6)(2x-6)$

$\text{C)} \ (x+7)(x-7)$

$\text{D)} \ (x-4y)(x+4y)$

zie oplossing

Omdat alle opmerkelijke gelijkheden in deze oefening vermenigvuldigingen van sommen met verschillen zijn, worden ze allemaal opgelost met dezelfde formule:

$(a+b)\cdot (a-b) =a^2-b^2$

$\text{A)} \ \begin{aligned}(x+5)(x-5) &=x^2-5^2\\[2ex] & = \bm{x^2-25}\end{aligned}$

$\text{B)} \ \begin{aligned}(2x+6)(2x-6) & =(2x)^2-6^2 \\[2ex] & = \bm{4x^2-36}\end{aligned}$

$\text{C)} \ \begin{aligned}(x+7)(x-7) & =x^2-7^2 \\[2ex] & = \bm{x^2-49}\end{aligned}$

$\text{D)} \ \begin{aligned}(x-4y)(x+4y) & =(x+4y)(x-4y) \\[2ex] & =x^2-(4y)^2\\[2ex] & = \bm{x^2-16y^2}\end{aligned}$

Oefening 4

Los alle volgende opmerkelijke identiteiten op:

$\text{A)} \ \left(x^2+10\right)\left(x^2-10\right)$

$\text{B)} \ \left(4x^2+2y^3\right)^2$

$\text{C)} \ \left(6x^3-4y^4\right)^2$

$\text{D)} \ \left(8x^3+y^2\right)\left(8x^3-y^2\right)$

$\text{E)} \ \left(5x^2-9x\right)^2$

zie oplossing

$\text{A)} \ \begin{aligned}\left(x^2+10\right)\left(x^2-10\right) & =\left(x^2\right)^2-10^2\\[2ex] & = \bm{x^4-100}\end{aligned}$

$\text{B)} \ \begin{aligned}\left(4x^2+2y^3\right)^2 & =\left(4x^2\right)^2+2\cdot 4x^2\cdot 2y^3 +\left(2y^3\right)^2\\[2ex] & = \bm{16x^4+16x^2y^3+4y^6}\end{aligned}$

$\text{C)} \ \begin{aligned}\left(6x^3-4y^4\right)^2 & =\left(6x^3\right)^2-2\cdot 6x^3\cdot 4y^4 +\left(4y^4\right)^2 = \\[2ex] &= \bm{36x^6-48x^3y^4+16y^8}\end{aligned}$

$\text{D)} \ \begin{aligned}\left(8x^3+y^2\right)\left(8x^3-y^2\right) & =\left(8x^3\right)^2-\left(y^2\right)^2 \\[2ex] & = \bm{64x^6-y^4}\end{aligned}$

$\text{E)} \ \begin{aligned}\left(5x^2-9x\right)^2 & =\left(5x^2\right)^2-2\cdot 5x^2\cdot 9x +\left(9x\right)^2 \\[2ex] & = \bm{25x^4-90x^3+81x^2}\end{aligned}$

Oefening 5

Bereken de volgende opmerkelijke producten:

$\text{A)} \ (x+4)^3$

$\text{B)} \ \left(x^2-5\right)^3$

$\text{C)} \ \left(2x-1\right)^3$

$\text{D)} \ (5x+2)^3$

zie oplossing

Om alle opmerkelijke producten van het probleem te vinden, is het noodzakelijk om de formules voor een som en een verschil toe te passen, gekubeerd volgens de gevallen:

$(a+b)^3 = a^3+3a^2b+3ab^2 +b^3$

$(a-b)^3 = a^3-3a^2b+3ab^2-b^3$

$\text{A)} \ \begin{aligned}(x+4)^3& =x^3+3\cdot x^2\cdot 4 +3\cdot x\cdot 4^2+4^3\\[2ex] & =x^3+3\cdot x^2\cdot 4 +3\cdot x\cdot 16+64 \\[2ex] & = \bm{x^3+12x^2+48x+64}\end{aligned}$

$\text{B)} \ \begin{aligned}\left(x^2-5\right)^3& =\left(x^2\right)^3-3\cdot \left(x^2\right)^2\cdot 5 +3\cdot x^2\cdot 5^2-5^3\\[2ex] & =x^6-3\cdot x^4\cdot 5 +3\cdot x^2\cdot 25-125 \\[2ex] & = \bm{x^6-15x^4+75x^2-125}\end{aligned}$

$\text{C)} \ \begin{aligned}\left(2x-1\right)^3& =\left(2x\right)^3-3\cdot \left(2x\right)^2\cdot 1 +3\cdot 2x\cdot 1^2-1^3\\[2ex] & =8x^3-3\cdot 4x^2\cdot 1 +3\cdot 2x\cdot 1-1 \\[2ex] & = \bm{8x^3-12x^2+6x-1}\end{aligned}$

$\text{D)} \ \begin{aligned}(5x+2)^3& =(5x)^3+3\cdot \left(5x\right)^2\cdot 2 +3\cdot 5x\cdot 2^2+2^3\\[2ex] & =125x^3+3\cdot 25x^2\cdot 2 +3\cdot 5x\cdot 4+8 \\[2ex] & = \bm{125x^3+150x^2+60x+8}\end{aligned}$

Oefening 6

Los de volgende opmerkelijke gelijkheden op:

$\text{A)} \ \left(x^2+x+5\right)^2$

$\text{B)} \ \left(x^2+3x-4\right)^2$

$\text{C)} \ \left(4x^2-6x+3\right)^2$

$\text{D)} \ \left(x^3-3x^2-9x\right)^2$

zie oplossing

Om al deze opmerkelijke identiteiten op te lossen, moeten we de formule gebruiken voor het kwadraat van een trinominaal, namelijk:

$(a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc$

$\text{A)} \ \begin{array}{l} \left(x^2+x+5\right)^2 = \\[2ex] = \left(x^2\right)^2+x^2+5^2+2\cdot x^2 \cdot x + 2 \cdot x^2 \cdot 5 +2 \cdot x \cdot 5 = \\[2ex] = x^4+x^2+25+2x^3 + 10x^2 +10x = \\[2ex] = \bm{x^4+2x^3+11x^2+10x+25} \end{array}$

$\text{B)} \ \begin{array}{l}\left(x^2+3x-4\right)^2 = \\[2ex] = \left(x^2\right)^2+(3x)^2+(-4)^2+2\cdot x^2 \cdot 3x + 2 \cdot x^2 \cdot (-4) +2 \cdot 3x \cdot (-4) = \\[2ex] = x^4+9x^2+16+6x^3-8x^2-24x = \\[2ex] = \bm{x^4+6x^3+x^2-24x+16} \end{array}$

$\text{C)} \ \begin{array}{l}\left(4x^2-6x+3\right)^2 = \\[2ex] = \left(4x^2\right)^2+(-6x)^2+3^2+2\cdot 4x^2 \cdot (-6x) + 2 \cdot 4x^2 \cdot 3 +2 \cdot (-6x) \cdot 3 = \\[2ex] = 16x^4+36x^2+9-48x^3+24x^2-36x = \\[2ex] = \bm{16x^4-48x^3+60x^2-36x+9} \end{array}\end{array}$

$\text{D)} \ \begin{array}{l} \left(x^3-3x^2-9x\right)^2 = \\[2ex] = \left(x^3\right)^2+\left(-3x^2\right)^2+(-9x)^2+2\cdot x^3 \cdot (-3x^2) + 2 \cdot x^3 \cdot (-9x) +2 \cdot (-3x^2) \cdot (-9x) = \\[2ex] = x^6+9x^4+81x^2-6x^5-18x^4+54x^3 = \\[2ex] = \bm{x^6-6x^5-9x^4+54x^3+81x^2} \end{array}$

Oefening 7

Bereken de volgende opmerkelijke identiteiten met wortels en breuken (hoge moeilijkheidsgraad):

$\text{A)} \ \displaystyle \left(\sqrt{2x}-\sqrt{8x}\right)^2$

$\text{B)} \ \displaystyle \left(\frac{1}{2}x^2+\frac{5}{3}x\right)\left(\frac{1}{2}x^2-\frac{5}{3}x\right)$

$\text{C)} \ \displaystyle \left(\frac{4}{3}x^2+\frac{3}{2}x\right)^2$

$\text{D)} \ \Bigl(9x^3+\sqrt{5x}\Bigr)\Bigl(9x^3-\sqrt{5x}\Bigr)$

zie oplossing

Sectie A) bestaat uit een kwadratische aftrekking, dus om dit op te lossen moet de overeenkomstige formule worden toegepast en bovendien moet er rekening mee worden gehouden dat als een wortel in het kwadraat is, deze vereenvoudigd wordt:

$\text{A)} \ \begin{aligned}\left(\sqrt{2x}-\sqrt{8x}\right)^2 & =\left(\sqrt{2x}\right)^2-2\cdot \sqrt{2x}\cdot \sqrt{8x} +\left(\sqrt{8x}\right)^2\\[2ex] & =2x-2\sqrt{2x\cdot 8x} +8x \\[2ex] & = 10x-2\sqrt{16x^2} \\[2ex] &= 10x-2\cdot 4x = \\[2ex] & = 10x -8x \\[2ex] & = \bm{2x}\end{aligned}$

Sectie B) gaat over optellen door aftrekken en monomials hebben breukcoëfficiënten, waarmee dit opmerkelijke product moet worden bepaald met behulp van de formule voor optellen door aftrekken en de eigenschappen van breuken:

$\text{B)} \ \begin{aligned}\displaystyle \left(\frac{1}{2}x^2+\frac{5}{3}x\right)\left(\frac{1}{2}x^2-\frac{5}{3}x\right) & \displaystyle =\left(\frac{1}{2}x^2\right)^2-\left(\frac{5}{3}x\right)^2\\[4ex] \displaystyle & =\frac{1^2}{2^2}x^4-\frac{5^2}{3^2}x^2\\[4ex]\displaystyle & = \mathbf{\frac{1}{4}}\bm{x^4-}\mathbf{\frac{25}{9}}\bm{x^2} \end{aligned}$

De opmerkelijke gelijkheid in sectie C) is een som verhoogd tot 2 en is eveneens samengesteld uit breuken. Om dit te berekenen moeten we daarom de formule gebruiken voor een kwadratische som plus de eigenschappen van breuken:

$\text{C)} \ \displaystyle \begin{aligned} \left(\frac{4}{3}x^2+\frac{3}{2}x\right)^2 & = \left(\frac{4}{3}x^2\right)^2+2\cdot \frac{4}{3}x^2\cdot \frac{3}{2}x +\left(\frac{3}{2}x\right)^2\\[2ex] & = \frac{4^2}{3^2}x^4+2\cdot \frac{12}{6}x^3 +\frac{3^2}{2^2}x^2 \\[2ex] &= \frac{16}{9}x^4 +2\cdot 2x^3+\frac{9}{4}x^2 \\[2ex] & = \mathbf{\frac{16}{9}} \bm{x^4+4x^3+}\mathbf{\frac{9}{4}}\bm{x^2}\end{aligned}$

De laatste opmerkelijke identiteit gaat over een som maal een verschil met irrationele coëfficiënten, dus passen we de formule toe voor een som maal een verschil en vereenvoudigen vervolgens de kwadratische wortels:

$\text{D)} \ \begin{aligned}\Bigl(9x^3+\sqrt{5x}\Bigr)\Bigl(9x^3-\sqrt{5x}\Bigr) & =\Bigl(9x^3\Bigr)^2-\left(\sqrt{5x}\right)^2\\[2ex] & = \bm{81x^6-5x}\end{aligned}$

Andere opmerkelijke identiteitstypen

Alle opmerkelijke identiteiten die we hierboven hebben besproken, zijn de meest gebruikte. In de wiskunde zijn er echter nog andere opmerkelijke productsoorten die ook interessant zijn om te weten, omdat ze voor verschillende doeleinden worden gebruikt.

som van kubussen

De som van de kubussen komt overeen met een binomiaal waarvan de twee termen positief zijn en bovendien de kubieke wortels exact zijn. Daarom is de algebraïsche uitdrukking voor een som van kubussen a ³ +b ³ .

opmerkelijke identiteiten, producten of banden opgelost

De formule voor dit opmerkelijke product wordt gebruikt om een polynoom in factoren te ontbinden, dat wil zeggen: via de formule transformeren we een polynoom in een product van een binomiaal door een trinominaal.

Dus je kunt zien hoe het werkt. Hier is een voorbeeldtoepassing van deze opmerkelijke identiteit:

$x^3+8$

De vorige uitdrukking bestaat inderdaad uit een optelling van kubussen omdat de derdemachtswortel van de monomiaal is

$x^3$

is exact (geeft geen decimaal getal) en het getal 8 ook:

$\sqrt[3]{x^3} = x$

$\sqrt[3]{8} = 2$

$x^3+8=x^3+2^3$

Daarom kunnen we de formule voor de som van perfecte kubussen gebruiken om de kubieke uitdrukking om te zetten in een product van een binomiaal door een trinominaal:

$a^3+b^3 = (a+b)(a^2-ab+b^2)$

$\begin{aligned} x^3 +2^3 & = (x+2)(x^2-x \cdot 2 + 2^2) \\[2ex] & = (x+2)(x^2-2x + 4) \end{aligned}$

verschil in kubussen

Het verschil (of aftrekken) van kubussen is een binominale term die bestaat uit een positieve term en een negatieve term waarvan de kubieke wortels exact zijn. Met andere woorden, een kubusverschil wordt uitgedrukt in de vorm a ³ -b ³ .

Opgeloste oefeningen voor het ontbinden van polynomen met opmerkelijke identiteiten

Laten we een voorbeeld maken, zodat u kunt zien hoe dit opmerkelijke identiteitstype wordt opgelost:

$x^3-27$

Het is een kubusverschil omdat zowel de kubieke wortel van de monomial is

$x^3$

aangezien 27 correct zijn:

$\sqrt[3]{x^3} = x$

$\sqrt[3]{27} = 3$

$x^3-27=x^3-3^3$

Je kunt daarom de formule voor het verschil tussen perfecte kubussen gebruiken om de binomiaal te ontbinden:

$a^3-b^3 = (a-b)(a^2+ab+b^2)$

$\begin{aligned} x^3 -3^3 & = (x-3)(x^2+x \cdot 3 + 3^2) \\[2ex] & =(x-3)(x^2+3x + 9) \end{aligned}$

Product van binominale termen met een gemeenschappelijke term

Dit opmerkelijke product wordt gebruikt om een product van twee binomialen die een gemeenschappelijke term hebben, om te zetten in een kwadratische polynoom.

opmerkelijke identiteiten, producten of gelijkheden pdf

Hier is een uitgebreid voorbeeld van dit soort opmerkelijke producten:

$\begin{aligned} (x+4)(x+5) &= x^2+(4+5)x+4\cdot 5 \\[2ex] & = x^2+9x+20 \end{aligned}$

meer identiteiten

Hoewel opmerkelijke identiteiten het meest bekend zijn omdat ze het meest voorkomen, moet worden opgemerkt dat er ook meer identiteiten met andere namen zijn. Hier is een lijst met andere, minder bekende identiteiten, voor het geval je nieuwsgierig bent:

Lagrange-identiteiten:

$(a^2+b^2)\cdot (x^2+y^2) =(ax+by)^2+(ay-bx)^2$
$(a^2-b^2)\cdot (x^2-y^2) =(ax+by)^2-(ay+bx)^2$

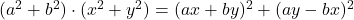
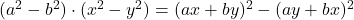
Legendre identiteiten:

$(a+b)^2+(a-b)^2=2(a^2+b^2)$
$(a+b)^2-(a-b)^2=4ab$
$(a+b)^4-(a-b)^4=8ab(a^2+b^2)$

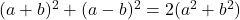
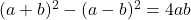
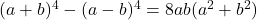
Argands identiteit:

$(x^2+x+1)(x^2-x+1) = x^4+x^2+1$

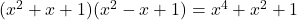
Gaussiaanse identiteiten:

$a^3+b^3+c^3-3abc= (a+b+c)(a^2+b^2+c^2-ab-bc-ac)$
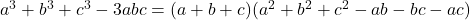
$a^3+b^3+c^3-3abc= \frac{1}{2} (a+b+c)\left[(a-b)^2+(b-c)^2+(a-c)^2\right]$

Opmerkelijke identiteits-apps

Als je zo ver bent gekomen, betekent dit dat je al weet hoe je berekeningen met opmerkelijke identiteiten moet uitvoeren. Helder! Maar echt… waar dienen opmerkelijke identiteiten voor? En wanneer worden opmerkelijke identiteiten gebruikt?

Zoals we in dit artikel hebben gezien, is het belangrijkste doel van opmerkelijke identiteiten het vereenvoudigen van berekeningen. Dat wil zeggen dat we dankzij opmerkelijke producten bepaalde machten van complexe polynomen direct kunnen oplossen zonder moeilijke bewerkingen uit te hoeven voeren.

Maar opmerkelijke gelijkheden hebben ook andere functies, zoals het ontbinden van polynomen en het invullen van kwadraten. Vervolgens zullen we zien waaruit elk van deze applicaties bestaat.

Veeltermen ontbinden in factoren

Sommige zeer specifieke soorten polynomen kunnen worden gecombineerd met opmerkelijke identiteiten. Als we bijvoorbeeld een polynoom vinden dat is samengesteld uit twee termen die perfecte kwadraten zijn (hun vierkantswortels zijn exact), kunnen we deze ontbinden in factoren met behulp van de opmerkelijke gelijkheidsformule van het product van een som met een verschil:

$a^2-b^2 =(a+b)(a-b)$

$x^2-9 =(x+3)(x-3)$

Op dezelfde manier kunnen trinomialen die de opmerkelijke identiteit van het kwadraat van een optelling of aftrekking respecteren, worden ontbonden in factoren:

$a^2+2ab+b^2=(a+b)^2$

$x^2+4x+4=(x+2)^2$

$a^2-2ab+b^2=(a-b)^2$

$x^2-10x+25=(x-5)^2$

Op dezelfde manier kunnen, zodra een polynoom in factoren is verwerkt, de wortels (of nullen) van dat polynoom worden gevonden. Toch is dit concept iets ingewikkelder om te begrijpen, dus als je meer geïnteresseerd bent, raden we je aan de uitleg in de zoekmachine op onze website (rechtsboven) te zoeken, aangezien we een heel artikel hebben waarin dit wordt uitgelegd.

vierkante voltooiing

Het invullen van kwadraten is een wiskundige procedure die wordt gebruikt om een kwadratische trinominaal om te zetten in de som van een kwadraat plus (of min) een getal.

Gegeven elke trinominaal:

$ax^2+bx+c$

Vervolgens kan de trinominaal worden omgezet in de volgende uitdrukking:

$a(x+h)^2+k$

waar de parameters

$h$

$k$

worden berekend met de volgende formules:

$h=\cfrac{b}{2a} \qquad \qquad k=c-ah^2$

Zelfs als het je niet zo lijkt, zijn deze twee formules afgeleid van opmerkelijke identiteiten. Dankzij de opmerkelijke producten kunnen de vierkanten dus worden voltooid.

Als voorbeeld zullen we deze procedure toepassen op de volgende trinominaal:

$2x^2+4x+3$

We berekenen de parameters

$h$

$k:$

$h=\cfrac{b}{2a}=\cfrac{4}{2\cdot 2} =1$

$k=c-ah^2 = 3-2\cdot 1^2 = 1$

En daarom blijft de polynoom:

$2(x+1)^2+1$

Wat zijn opmerkelijke identiteiten (of opmerkelijke producten)?

Opmerkelijke identiteitsformules (of producten)

kwadraat van een som

Voorbeeld:

kwadraat van een verschil

Voorbeeld:

som per verschil

Voorbeeld:

kwadraat van een trinominaal

Voorbeeld:

Opmerkelijke identiteiten (of producten) in blokjes

kubus van een som

Voorbeeld:

kubus van een verschil

Voorbeeld:

Overzichtstabel van opmerkelijke identiteiten

Opgeloste oefeningen van opmerkelijke identiteiten (of producten)

Oefening 1

Oefening 2

Oefening 3

Oefening 4

Oefening 5

Oefening 6

Oefening 7

Andere opmerkelijke identiteitstypen

som van kubussen

verschil in kubussen

Product van binominale termen met een gemeenschappelijke term

meer identiteiten

Opmerkelijke identiteits-apps

Veeltermen ontbinden in factoren

vierkante voltooiing

Laat een reactie achter Reactie annuleren