Hier vindt u alles over hyperbool: wat het is, wat de karakteristieke elementen ervan zijn, hoe u de vergelijking kunt vinden, voorbeelden, opgeloste oefeningen, enz.
Wat is hyperbool?
De hyperbool is een open curve met twee takken, waarvan de wiskundige definitie als volgt is:
In de analytische meetkunde is een hyperbool de verzameling punten op het vlak die aan de volgende voorwaarde voldoet: de absolute waarde van het verschil in afstanden tussen elk punt van de hyperbool en twee vaste punten (de zogenaamde brandpunten) moet constant zijn.
Bovendien is de waarde van het aftrekken van deze twee afstanden altijd gelijk aan de afstand tussen de twee hoekpunten van de hyperbool.
![]()

Hieronder zullen we zien wat de coëfficiënt betekent
![]()
van een hyperbool.
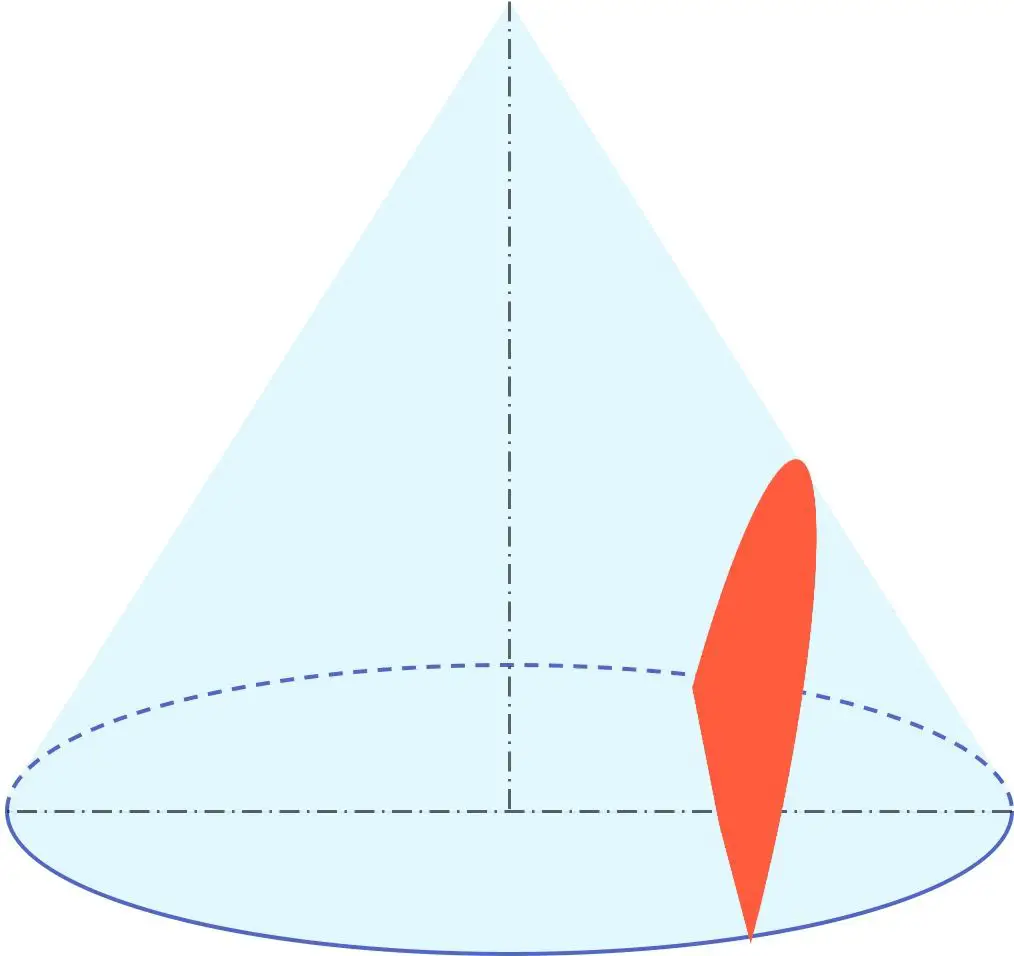
Bovendien maakt de hyperbool deel uit van de geometrische groep die kegelsneden wordt genoemd, samen met de omtrek, de ellips en de parabool. Daarom is een hyperbool een kegelsnede, of met andere woorden, deze kan worden verkregen uit een kegel.
In het bijzonder is een hyperbool het resultaat van de doorsnede van een kegel door een vlak met een hoek die kleiner is dan de hoek gevormd door de generator van de kegel ten opzichte van zijn omwentelingsas.
Elementen van een hyperbool
De kenmerken van een hyperbool zijn afhankelijk van het volgende:
- De brandpunten : dit zijn twee vaste punten die kenmerkend zijn voor elke hyperbool (punten F en F’ in de onderstaande grafiek). De absolute waarde van het verschil tussen de afstanden van elk punt van de hyperbool tot elk brandpunt is constant en gelijk aan

- Brandpunt of hoofdas : het is de lijn die door de twee brandpunten van de hyperbool loopt. Het komt overeen met een symmetrieas van genoemde geometrische figuur. Ook wel dwars- of dwarsas genoemd.
- Secundaire as : het is de bissectrice van het segment FF’ (lijn die door de punten B en B’ loopt). Bovendien is het een lijn loodrecht op de brandpuntsas en is het een andere symmetrieas van de hyperbool
- Centrum (O) : is het snijpunt van de twee assen en het middelpunt van de twee hoekpunten en de twee brandpunten. Omdat de hyperbool twee symmetrieassen heeft, is deze ook het symmetriecentrum.
- Hoekpunten (A en A’) : zijn de snijpunten van de takken van de hyperbool met de brandpuntsas.
- Vectorstralen (R) : dit zijn de segmenten die van elk punt op de hyperbool naar elk brandpunt gaan.
- Brandpuntsafstand : dit is de lengte van het samengestelde segment tussen de twee brandpunten.
- Hoofdas of reële as: het is het segment dat van punt A naar punt A gaat, de lengte is gelijk aan

- Kleine as of denkbeeldige as: het is het segment dat van punt B naar punt B gaat, de lengte is gelijk aan
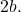
- Asymptoten : zijn de stippellijnen die in de grafiek worden weergegeven. Hoe ze worden berekend, zullen we hieronder zien.
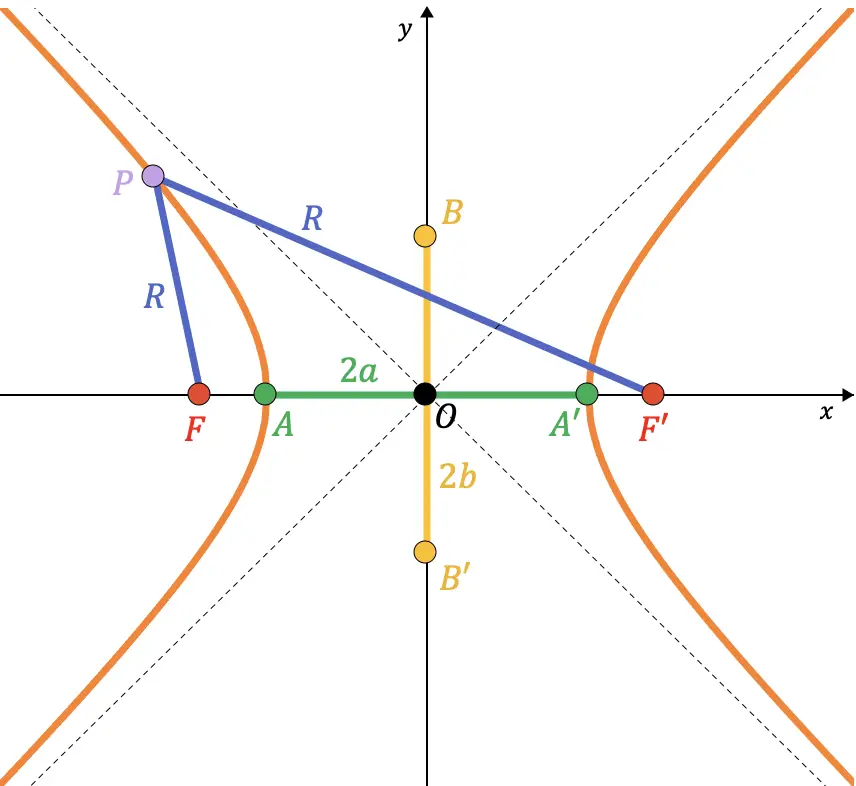
Relatie tussen de elementen van een hyperbool
Allereerst zeggen we dat halve as de helft van een as betekent. De echte halve as is bijvoorbeeld het segment dat van punt A naar het midden van de hyperbool gaat, waarvan de lengte gelijk is aan
![]()
Er is dus een zeer belangrijke relatie tussen de werkelijke halve as, de denkbeeldige halve as en de halve brandpuntsafstand. In feite wordt de formule die we hierna gaan afleiden veel gebruikt om hyperbooloefeningen en -problemen op te lossen.
U moet weten dat de punten B en B’ van een hyperbool overeenkomen met de snijpunten van de hoofdas en de denkbeeldige straalcirkel
![]()
(semi-brandpuntsafstand) van het middelpunt naar punt A. Daarom, zoals u kunt zien in de volgende grafische weergave, valt het segment dat punt A en punt B verbindt samen met de straal van genoemde cirkel (
![]()
):
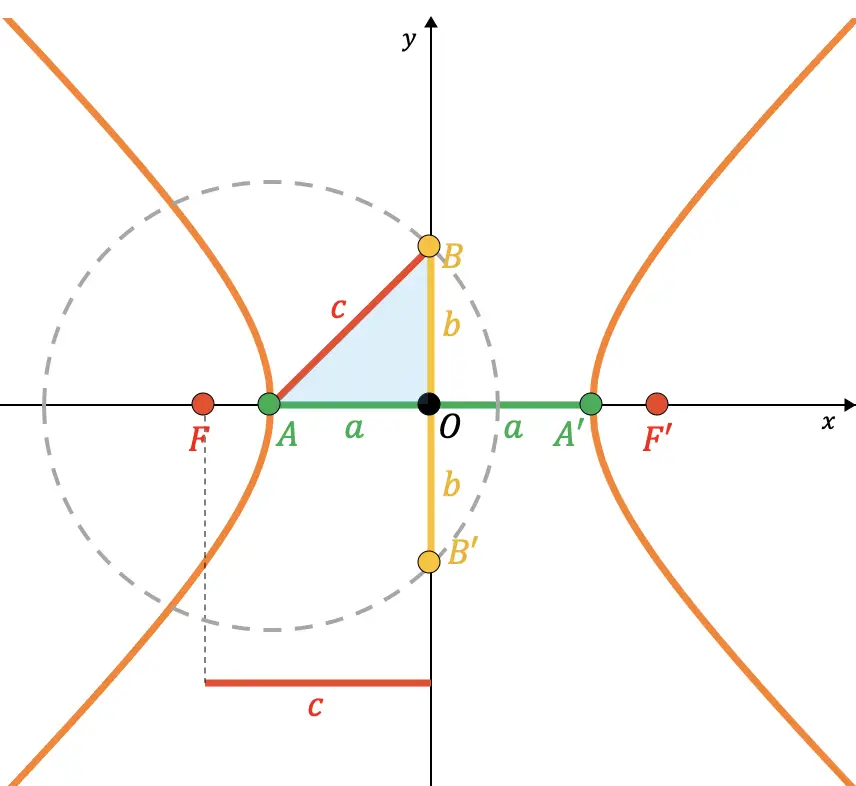
Uit de stelling van Pythagoras kan dus worden aangetoond dat de relatie tussen de parameters
![]()
En
![]()
is de volgende:
![]()
hyperbool vergelijking
Er zijn verschillende soorten hyperboolvergelijkingen, omdat afhankelijk van de eigenschappen de ene of de andere wordt gebruikt om het wiskundig uit te drukken. Vervolgens zullen we ze allemaal in detail analyseren.
Ten eerste hebben we de gewone vergelijking van de hyperbool. Ten tweede zullen we een variant van de gewone vergelijking zien, dit is de gereduceerde of canonieke vergelijking van de hyperbool. Vervolgens zullen we bestuderen hoe de algemene vergelijking van een hyperbool is. En ten slotte zullen we de vergelijkingen van twee speciale gevallen van hyperbolen analyseren: de gelijkzijdige hyperbool en de geconjugeerde hyperbolen .
Gewone vergelijking van de hyperbool
Wanneer we door een vergelijking een hyperbool willen definiëren met een buitencentrum op de oorsprong van de coördinaten (punt (0,0)), moeten we de volgende formule gebruiken:
De formule voor de gewone vergelijking van de hyperbool in cartesiaanse coördinaten is als volgt:
![]()
Goud:
-

En

zijn de coördinaten van het middelpunt van de hyperbool:
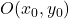
-

is de lengte van de halve lange as van de hyperbool.
-

is de lengte van de halve korte as van de hyperbool.
Met deze vergelijking kun je hyperbolen beschrijven waarvan de brandpuntsas horizontaal is (takken open naar links en rechts), wat hyperbolen normaal gesproken zijn. Maar als we werken met een verticale brandpuntsas (takken open van boven naar beneden), gaat het negatieve teken over van de variabele y naar de variabele x :
![]()
Goud
![]()
En
![]()
zijn, zoals voorheen, de coördinaten van het middelpunt van de hyperbool en de termen
![]()
En
![]()
ze zijn nog steeds de semi-hoofdas en de semi-kleine as van de hyperbool, hoewel deze twee nu, in tegenstelling tot voorheen, respectievelijk verticaal en horizontaal georiënteerd zullen zijn.
Canonieke of gereduceerde vergelijking van de hyperbool
Dit type hyperboolvergelijking lijkt sterk op de gewone vergelijking. Het enige verschil is dat de canonieke vergelijking wordt gebruikt om hyperbolen analytisch uit te drukken waarvan het middelpunt het punt (0,0) is. Daarom gebruiken we de canonieke of gereduceerde vergelijking van de hyperbool wanneer het midden van de hyperbool de oorsprong van de coördinaten is.
We zullen nu de formule voor de gereduceerde vergelijking van de hyperbool afleiden uit de gewone vergelijking:
![]()
Als het middelpunt van de hyperbool de oorsprong van de coördinaten zou moeten zijn, dat wil zeggen het punt (0,0), zal het volgende altijd waar zijn:
![]()
![]()
De canonieke of gereduceerde vergelijkingsformule van de hyperbool zal dus zijn:
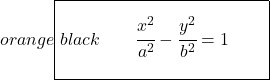
Als de brandpuntsas verticaal zou zijn in plaats van horizontaal, zou de negatieve variabele, net als voorheen, x zijn:
![]()
Algemene vergelijking van de hyperbool
De formule voor de algemene vergelijking van een hyperbool is als volgt:
![]()
Om de bovenstaande vergelijking echter een hyperbool te laten zijn, zijn de coëfficiënten
![]()
En
![]()
Ze moeten verschillend zijn van nul en tegelijkertijd het tegenovergestelde teken hebben.
Gelijkzijdige hyperboolvergelijking
Een gelijkzijdige hyperbool is een hyperbool waarbij de lengte van de werkelijke halve as gelijk is aan de lengte van de denkbeeldige halve as, dit betekent dat
![]()
Daarom is de vergelijking van een gelijkzijdige hyperbool:
![]()
Bovendien staan de asymptoten van de gelijkzijdige hyperbolen loodrecht op elkaar. En de vergelijkingen van deze lijnen zijn als volgt:
![]()
![]()
Als we goed kijken, zijn deze twee vergelijkingen de bissectrices van respectievelijk het eerste (en derde) kwadrant en het tweede (en vierde) kwadrant. Dus als we een gelijkzijdige hyperbool 45° naar links draaien, nemen de asymptoten de plaats in van de coördinaatassen:
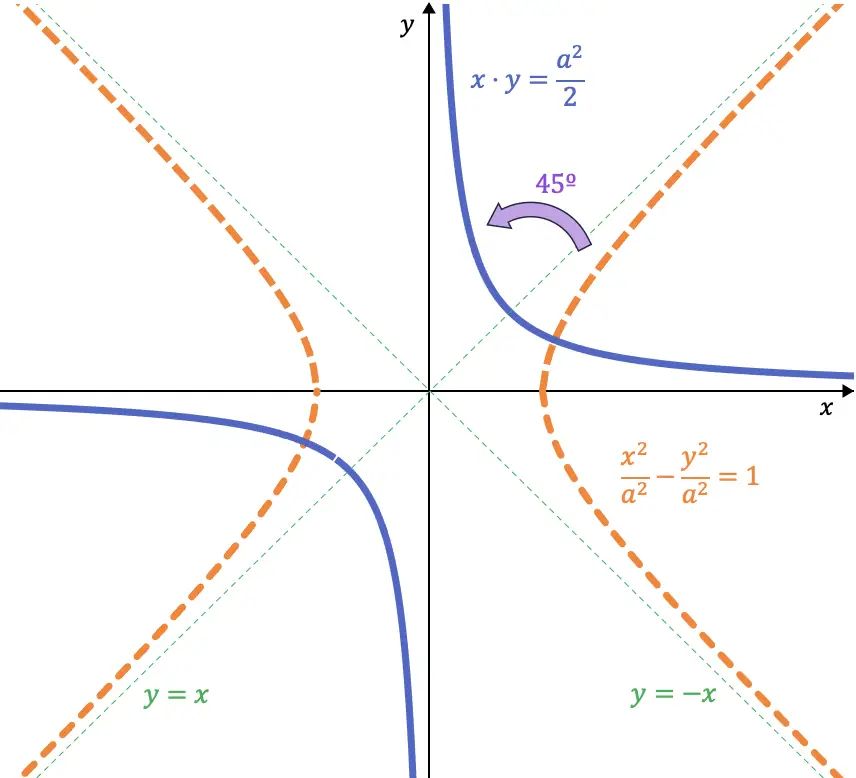
Dus als we een bocht van 45 graden maken, is de vergelijking voor de hyperbool:
![]()
geconjugeerde hyperbolen
Twee hyperbolen zijn geconjugeerd als de reële as van de ene equivalent is aan de denkbeeldige as van de andere . Daarom is het enige verschil tussen de vergelijkingen van twee geconjugeerde hyperbolen welke variabele wordt genegeerd, omdat de coëfficiënten van de noemers hetzelfde moeten blijven.
Hier is een voorbeeld van de vergelijkingen van twee hyperbolen die aan elkaar zijn geconjugeerd:
![]()
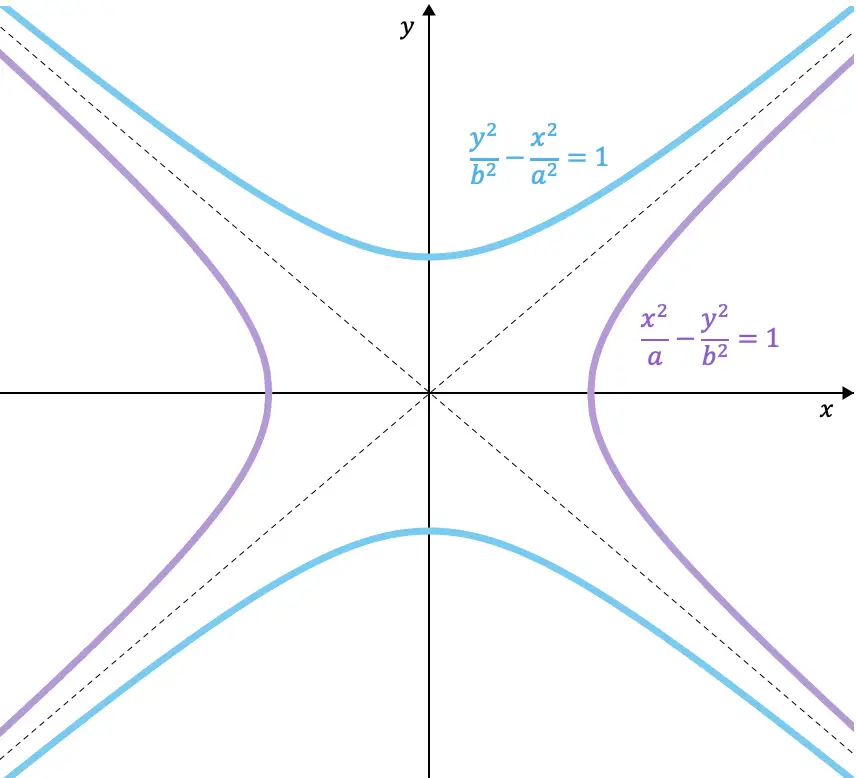
Bovendien delen de geconjugeerde hyperbolen, zoals u kunt zien aan de hand van de hyperbolen die in een grafiek zijn weergegeven, dezelfde asymptoten.
Asymptoten van de hyperbool
Zoals je in de vorige grafieken hebt gezien, heeft elke hyperbool twee asymptoten. Bedenk dat een asymptoot een rechte lijn is die een functie heel dicht benadert, maar deze nooit helemaal snijdt of raakt.
De formules die overeenkomen met de asymptoten van de hyperbolen zijn dus:
![]()
![]()
Zodat de asymptoten van elke hyperbool eenvoudig kunnen worden bepaald met behulp van hun coëfficiënten
![]()
En
![]()
die respectievelijk de lengtes zijn van de werkelijke halve as en de denkbeeldige halve as van de hyperbool.
Excentriciteit van de hyperbool
De excentriciteit van een hyperbool is een karakteristieke parameter die bepaalt hoe open of gesloten deze is. Numeriek wordt de excentriciteit van een hyperbool berekend door de halve brandpuntsafstand te delen door de werkelijke halve as:
![]()
De excentriciteit van elke hyperbool is altijd groter dan 1:
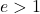
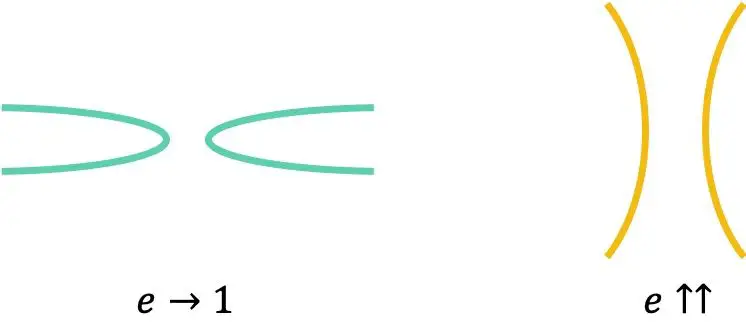
Ten slotte moet worden opgemerkt dat de excentriciteit van een gelijkzijdige hyperbool altijd gelijk is aan
![]()
Hyperboolproblemen opgelost
Hieronder kun je de concepten die we hebben gezien oefenen met problemen en opgeloste oefeningen van hyperbolen en de hyperboolvergelijking.
Oefening 1
Wat is de vergelijking van de hyperbool met het middelpunt op het punt (-1,3), de lengte van de echte halve as van 3 eenheden en de lengte van de denkbeeldige halve as (parallel aan de Y-as) van 7 eenheden?
Om de vergelijking van de hyperbool te vinden, past u eenvoudigweg de formule voor de gewone vergelijking van de hyperbool toe:
![]()
We vervangen de coördinaten van het middelpunt van de hyperbool in de vergelijking:
![]()
![]()
En ten slotte vervangen we de waarden van de onbekenden
![]()
En
![]()
![]()
![]()
Oefening 2
Vind de coördinaten van het centrum, de hoekpunten, de brandpunten, de waarde van de excentriciteit en de asymptoten van de hyperbool waarvan de vergelijking wordt gedefinieerd door:
![]()
Allereerst moet worden opgemerkt dat de negatieve variabele in de vergelijking de variabele y is, dus de takken van de hyperbool zullen naar rechts en naar links openen (brandpuntsas evenwijdig aan de X-as).
Ten tweede komt de vergelijking overeen met de canonieke (of gereduceerde) vergelijking van de hyperbool, dus het middelpunt is de oorsprong van de coördinaten.
![]()
Zodra we het middelpunt van de hyperbool kennen, moeten we, om al het andere te berekenen, de waarde van de echte halve as vinden (parameter
![]()
) en de denkbeeldige halve as (parameter
![]()
). We kunnen beide afleiden uit de formule van de canonieke (of gereduceerde) vergelijking van de hyperbool:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Dus als er een afstand van 5 eenheden is tussen het centrum en de hoekpunten, impliceert dit dat de hoekpunten van de hyperbolen zijn:
![]()
Om de coördinaten van elk brandpunt te bepalen, moet u de waarde van de halve brandpuntsafstand kennen (parameter
![]()
). En hiervoor kunnen we de formule gebruiken die de elementen van een hyperbool met elkaar verbindt:
![]()
![]()
![]()
Tussen het centrum en de woningen bevindt zich dus een ruimte van 13 eenheden. De coördinaten van elk huishouden zijn dus:
![]()
Om vervolgens de excentriciteit van de hyperbool te berekenen, moeten we de overeenkomstige formule gebruiken:
![]()
En ten slotte vinden we de asymptoten van de hyperbool met hun formules:
![]()
![]()
Oefening 3
Bereken de vergelijking van de hyperbool met het middelpunt op de oorsprong van de coördinaten, wetende dat het verschil in de afstanden van een punt van de hyperbool tot de brandpunten F(-4.0) en F(4.0) 6 eenheden is.
Omdat het middelpunt van de hyperbool zich in de oorsprong van de coördinaten bevindt, zullen we eerst de canonieke of gereduceerde vergelijking gebruiken:
![]()
Vervolgens moet, volgens de definitie van een hyperbool, de absolute waarde van het verschil in afstanden van een van zijn punten tot de brandpunten (in dit geval 6) gelijk zijn aan de lengte van de reële as (
![]()
). Nog:
![]()
![]()
![]()
![]()
Aan de andere kant is het middelpunt van de hyperbool het punt (0,0) en een focus is het punt (4,0). Zodat de afstand tot de twee punten (parameter
![]()
) zijn 4 eenheden.
![]()
We kunnen nu de waarde van de parameter kennen
![]()
met de wiskundige relatie tussen de 3 karakteristieke coëfficiënten van de hyperbool:
![]()
![]()
![]()
![]()
De vergelijking van de hyperbool is dus:
![]()
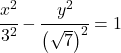
![]()