Hyperbolische sinusfunctie

In dit artikel vind je alles over de hyperbolische sinus: wat is de formule, de grafische weergave, al zijn kenmerken, de relaties met andere functies,…

Hyperbolische sinusformule

De hyperbolische sinusfunctie is een van de belangrijkste hyperbolische functies en wordt weergegeven door het symbool sinh(x) of sinh(x) . De hyperbolische sinus is gelijk aan e ^x minus e ^-x gedeeld door 2.

De formule voor de hyperbolische sinus is daarom als volgt:

$\displaystyle\text{senh}(x)=\cfrac{e^{x}-e^{-x}}{2}$

De hyperbolische sinus houdt dus verband met de exponentiële functie.

➤ Zie: kenmerken van de exponentiële functie

Grafische weergave van de hyperbolische sinus

Met behulp van de formule die we in de vorige sectie hebben gezien, kunnen we een tabel maken met de hyperbolische sinuswaarden en de functie in een grafiek zetten:

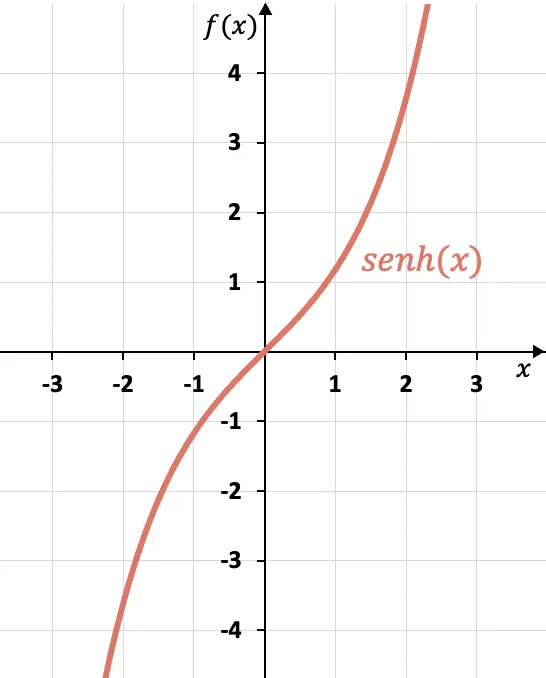
In deze grafiek kunnen we zien dat de hyperbolische sinus een vreemde functie is, omdat de tegenovergestelde x’s tegengestelde afbeeldingen hebben, of met andere woorden: de hyperbolische sinusgrafiek is symmetrisch ten opzichte van de oorsprong van de coördinaten (0, 0).

Zoals u kunt zien, is de hyperbolische sinusgrafiek heel anders dan die van de sinus, wat een periodieke functie is. Je kunt de grafische weergave van de sinus en alle verschillen met de hyperbolische sinus zien in de volgende link:

➤ Zie: Grafische weergave van de sinusfunctie

Kenmerken van de hyperbolische sinus

De hyperbolische sinus heeft de volgende eigenschappen:

Het domein van de hyperbolische sinusfunctie bestaat uit alle reële getallen:

$\text{Dom } f = \mathbb{R}$

Het bereik of bereik van de hyperbolische sinusfunctie zijn ook allemaal reële getallen.

$\text{Im } f= \mathbb{R}$

De hyperbolische sinus is een continue en oneven functie.

$\displaystyle \text{senh}(-x) =- \text{senh}(x)$

Onderschept de X-as en de Y-as op hetzelfde snijpunt, de coördinaatoorsprong:

$(0,0)$

De limiet van de hyperbolische sinusfunctie wanneer x neigt naar plus/min oneindig is gelijk aan plus/min oneindig:

$\displaystyle\lim_{x\to+\infty}\text{senh}(x)=+\infty$

$\displaystyle\lim_{x\to-\infty}\text{senh}(x)=-\infty$

De hyperbolische sinus neemt over het hele domein strikt toe en heeft dus geen maxima of minima.

Het verandert echter zijn kromming op het punt x = 0, dus het is een buigpunt van de functie. Voor waarden kleiner dan x=0 is het een concave functie, voor waarden groter dan x=0 is het daarentegen een convexe functie.

De afgeleide van de hyperbolische sinusfunctie is de hyperbolische cosinus:

$f(x)=\text{senh}(x) \ \longrightarrow \ f'(x)=\text{cosh}(x)$

Op dezelfde manier is de integraal van de hyperbolische sinusfunctie de hyperbolische cosinus:

$\displaystyle \int \text{senh}(x) \ dx= \text{cosh}(x) + C$

De Taylorreeks van de hyperbolische sinusfunctie is gelijk aan de volgende uitdrukking:

$\displaystyle\text{senh}(x)=x+\cfrac{x^3}{3!}+\cfrac{x^5}{5!}+\cfrac{x^7}{7!}+\dots=\sum_{n=0}^\infty\cfrac{x^{2n+1}}{(2n+1)!}$

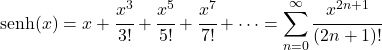
De Laplace-transformatie van de hyperbolische sinusfunctie is als volgt:

$\mathcal{L}\bigl[\text{senh}(at)\bigr]=\cfrac{a}{s^2-a^2}$

Wiskundige relaties van hyperbolische sinus

De hyperbolische sinus is gekoppeld aan de andere hyperbolische functies door de volgende vergelijkingen:

De fundamentele vergelijking relateert de hyperbolische sinus aan de hyperbolische cosinus:

$\text{cosh}^2(x)-\text{senh}^2(x)=1$

Daarom zijn de hyperbolische sinus- en cosinusfuncties gerelateerd aan de hyperboolvergelijking, namelijk x ² -y ² =1. In tegenstelling tot de trigonometrische sinus- en cosinusfuncties die met elkaar verbonden zijn door de cirkelvergelijking (x ² +y ² =1).

De hyperbolische functies van sinus, cosinus en tangens kunnen met elkaar in verband worden gebracht door de volgende vergelijking:

$\text{tanh}(x)=\cfrac{\text{senh}(x)}{\text{cosh}(x)}$

Aan de andere kant kan de hyperbolische sinus van het optellen of aftrekken van twee verschillende getallen worden berekend met de volgende formules:

$\text{senh}(x+y)=\text{senh}(x)\text{cosh}(y)+\text{senh}(y)\text{cosh}(x)$

$\text{senh}(x-y)=\text{senh}(x)\text{cosh}(y)-\text{senh}(y)\text{cosh}(x)$

De hyperbolische sinus van tweemaal een getal kan worden bepaald door de volgende wiskundige relatie toe te passen:

$\text{senh}(2x)=2\text{senh}(x)\text{cosh}(x)$

De som of aftrekking van twee hyperbolische sinussen kan worden gevonden met behulp van de volgende formules:

$\displaystyle\text{senh}(x)+\text{senh}(y)=2\text{senh}\left(\frac{x+y}{2}\right)\text{cosh}\left(\frac{x-y}{2}\right)$

$\displaystyle\text{senh}(x)-\text{senh}(y)=2\text{senh}\left(\frac{x-y}{2}\right)\text{cosh}\left(\frac{x+y}{2}\right)$

Ten slotte kan het kwadraat van de hyperbolische sinus worden berekend door de volgende formule toe te passen:

$\text{senh}^2(x)=\cfrac{1}{2}\Bigl(\text{cosh}(2x)-1\Bigr)$

Hyperbolische sinusformule

Grafische weergave van de hyperbolische sinus

Kenmerken van de hyperbolische sinus

Wiskundige relaties van hyperbolische sinus

Laat een reactie achter Reactie annuleren