Afgeleide van de hyperbolische sinus

Hier vindt u hoe u de hyperbolische sinus (formule) kunt afleiden. Bovendien ziet u verschillende opgeloste voorbeelden van de hyperbolische sinusderivaat. En ten slotte bewijzen we de formule voor de afgeleide van dit type trigonometrische functie.

Formule afgeleid van hyperbolische sinus

De afgeleide van de hyperbolische sinus van x is de hyperbolische cosinus van x.

$f(x)=\text{senh}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(x)$

Daarom is de afgeleide van de hyperbolische sinus van een functie gelijk aan het product van de hyperbolische cosinus van de functie en de afgeleide van die functie.

$f(x)=\text{senh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(u)\cdot u'$

Eigenlijk zijn de bovenstaande twee formules hetzelfde, het enige verschil is dat we in de tweede formule de kettingregel toepassen. En aangezien de afgeleide van x 1 is, verandert dit niets aan de functie.

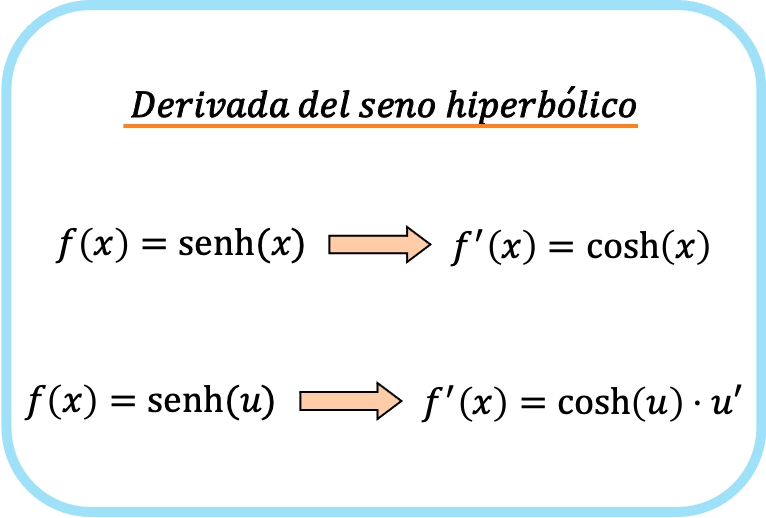
Zoals je kunt zien, lijkt de formule voor de hyperbolische sinusderivaat sterk op de formule voor de sinusderivaat .

Voorbeelden van de hyperbolische sinusderivaat

Nadat we al hebben gezien wat de formule van de hyperbolische sinusderivaat is, gaan we nu verder met het oplossen van verschillende voorbeelden van de hyperbolische sinusderivaat. U twijfelt dus zeker niet aan de manier waarop dit wordt gedaan.

Voorbeeld 1: Afgeleide van de hyperbolische sinus van 2x

$f(x)=\text{senh}(2x)$

In dit geval hebben we in het hyperbolische sinusargument een andere functie dan x. Daarom moeten we de hyperbolische sinusafgeleide formule met de kettingregel gebruiken om de afgeleide te vinden:

$f(x)=\text{senh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(u)\cdot u'$

De afgeleide van 2x is 2, dus de afgeleide van de hyperbolische sinus van 2x is de hyperbolische cosinus van 2x maal 2.

$f(x)=\text{senh}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(2x)\cdot 2=2\text{cosh}(2x)$

Voorbeeld 2: Afgeleide van de hyperbolische sinus van x kwadraat

$f(x)=\text{senh}(x^2)$

De formule voor de afgeleide van de hyperbolische sinusfunctie is:

$f(x)=\text{senh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(u)\cdot u'$

Aan de andere kant is de afgeleide van de kwadratische functie x ² 2x. De afgeleide van de gehele functie is daarom:

$f(x)=\text{senh}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(x^2)\cdot 2x$

Bewijs van de formule voor de afgeleide van de hyperbolische sinus

Ten slotte zullen we de formule voor de hyperbolische sinusderivaat demonstreren. Om dit te doen, zullen we uitgaan van de wiskundige definitie van de hyperbolische sinus:

$\text{senh}(x)=\cfrac{e^x-e^{-x}}{2}$