Hyperbolische cosinusfunctie

Hier vindt u alles over de hyperbolische cosinusfunctie: wat is de formule, de grafische weergave, de kenmerken ervan, de wiskundige relaties met andere functies, enz.

Hyperbolische cosinusformule

De hyperbolische cosinusfunctie is een van de belangrijkste hyperbolische functies en wordt weergegeven door het symbool cosh(x) . De hyperbolische cosinus is gelijk aan de som van e ^x plus e ^-x gedeeld door 2.

Daarom is de formule voor de hyperbolische cosinus:

$\displaystyle\text{cosh}(x)=\cfrac{e^{x}+e^{-x}}{2}$

De hyperbolische cosinus is dus wiskundig gerelateerd aan de exponentiële functie. In de volgende link kunt u de eigenschappen van dit type functie zien:

➤ Zie: eigenschappen van de exponentiële functie

Grafische weergave van de hyperbolische cosinus

De grafische weergave van de hyperbolische cosinusfunctie heeft de vorm van een kwadratische functie (of parabool):

➤ Zie: Grafische weergave van een kwadratische functie .

In deze grafiek kunnen we duidelijk zien dat de hyperbolische cosinus een even functie is, omdat deze symmetrisch is rond de y-as.

Aan de andere kant is de grafiek van de hyperbolische cosinus heel anders dan die van de cosinus (trigonometrische functie), die een periodieke functie is. U kunt de grafische weergave van de cosinus en alle verschillen met de hyperbolische cosinus zien in de volgende link:

➤ Zie: grafische weergave van de cosinusfunctie

Kenmerken van de hyperbolische cosinus

De hyperbolische cosinus respecteert de volgende eigenschappen:

Het domein van de hyperbolische cosinusfunctie bestaat uit alle reële getallen:

$\text{Dom } f = \mathbb{R}$

In plaats daarvan is het bereik (of bereik) van de hyperbolische cosinusfunctie 1 en alle getallen groter dan 1:

$\text{Im } f= [1,+\infty)$

De hyperbolische cosinus is een continue en even functie.

$\displaystyle \text{cosh}(-x)=\text{cosh}(x)$

De functie snijdt de Y-as in het punt x=0.

$(0,1)$

Aan de andere kant heeft de functie geen snijpunt met de X-as.

De twee grenzen tot oneindig (positief en negatief) van de hyperbolische cosinusfunctie geven plus oneindig.

$\displaystyle\lim_{x\to+\infty}\text{cosh}(x)=+\infty$

$\displaystyle\lim_{x\to-\infty}\text{cosh}(x)=+\infty$

De hyperbolische cosinus neemt af tot x = 0 en neemt vanaf dat punt oneindig toe, dus de functie heeft een minimum bij x = 0.

$(0,1)$

De functie is over het hele domein convex en heeft dus geen buigpunt.

De afgeleide van de hyperbolische cosinusfunctie is de hyperbolische sinus:

$f(x)=\text{cosh}(x) \ \longrightarrow \ f'(x)=\text{senh}(x)$

De integraal van de hyperbolische cosinusfunctie is de hyperbolische sinus:

$\displaystyle \int \text{cosh}(x) \ dx= \text{senh}(x) + C$

Het Taylor-polynoom (of Maclaurin-reeks) van de hyperbolische cosinusfunctie is als volgt:

$\displaystyle\text{cosh}(x)=1+\cfrac{x^2}{2!}+\cfrac{x^4}{4!}+\cfrac{x^6}{6!}+\dots=\sum_{n=0}^\infty\cfrac{x^{2n}}{(2n)!}$

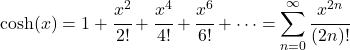
De Laplace-transformatie van de hyperbolische cosinusfunctie is als volgt:

$\mathcal{L}\bigl[\text{cosh}(at)\bigr]=\cfrac{s}{s^2-a^2}$

Wiskundige relaties van hyperbolische cosinus

Vervolgens zullen we zien hoe de hyperbolische cosinus kan worden berekend op basis van andere hyperbolische functies, aangezien ze allemaal wiskundig gerelateerd zijn.

De fundamentele vergelijking relateert de hyperbolische cosinus aan de hyperbolische sinus:

$\text{cosh}^2(x)-\text{senh}^2(x)=1$

➤ Zie: hyperbolische sinus

De drie belangrijkste hyperbolische functies (hyperbolische sinus, cosinus en tangens) kunnen met elkaar in verband worden gebracht door de volgende vergelijking:

$\text{tanh}(x)=\cfrac{\text{senh}(x)}{\text{cosh}(x)}$

Aan de andere kant kan de hyperbolische cosinus van het optellen (of aftrekken) van twee verschillende getallen worden bepaald met de volgende formules:

$\text{cosh}(x+y)=\text{cosh}(x)\text{cosh}(y)+\text{senh}(y)\text{senh}(x)$

$\text{cosh}(x-y)=\text{cosh}(x)\text{cosh}(y)-\text{senh}(y)\text{senh}(x)$

De hyperbolische cosinus van tweemaal een getal is gelijk aan de som van de kwadraten van de hyperbolische cosinus en de hyperbolische sinus van dit getal:

$\text{cosh}(2x)=\text{cosh}^2(x)+\text{senh}^2(x)$

Het optellen of aftrekken van twee hyperbolische cosinussen kan worden berekend door de volgende formules toe te passen:

$\displaystyle\text{cosh}(x)+\text{cosh}(y)=2\text{cosh}\left(\frac{x+y}{2}\right)\text{cosh}\left(\frac{x-y}{2}\right)$

$\displaystyle\text{cosh}(x)-\text{cosh}(y)=2\text{senh}\left(\frac{x+y}{2}\right)\text{senh}\left(\frac{x-y}{2}\right)$

Ten slotte kan het kwadraat van de hyperbolische cosinus worden berekend met de volgende formule:

$\text{cosh}^2(x)=\cfrac{1}{2}\Bigl(\text{cosh}(2x)+1\Bigr)$

Hyperbolische cosinusformule

Grafische weergave van de hyperbolische cosinus

Kenmerken van de hyperbolische cosinus

Wiskundige relaties van hyperbolische cosinus

Laat een reactie achter Reactie annuleren