Afgeleide van hyperbolische boogcosinus

Op deze pagina ziet u wat de afgeleide is van de hyperbolische boogcosinus (formule). Je vindt ook oefeningen die stap voor stap worden opgelost voor afgeleiden van de hyperbolische boogcosinus van een functie. En ten slotte vind je de demonstratie van de formule voor de afgeleide van dit type trigonometrische functie.

Formule voor de afgeleide van de hyperbolische boogcosinus

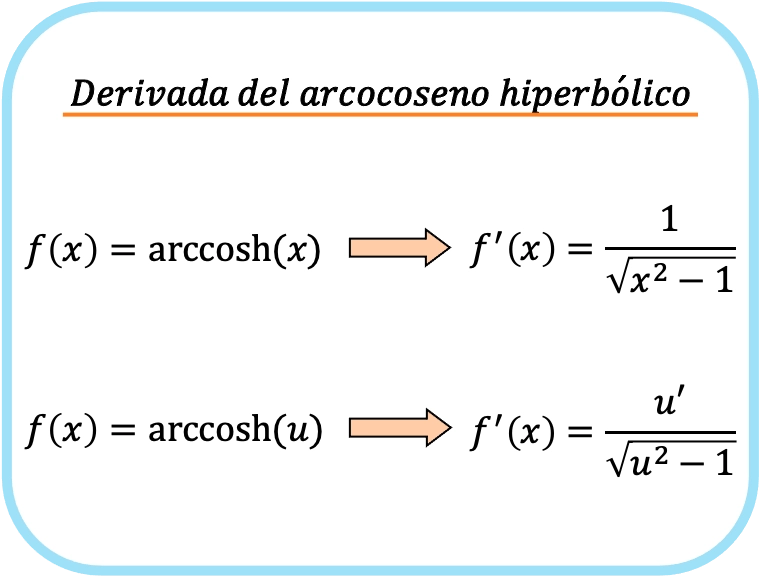
De afgeleide van de hyperbolische arccosinus van x is één gedeeld door de wortel van x in het kwadraat min 1.

f(x)=\text{arccosh}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{1}{\sqrt{x^2-1}}

Daarom is de afgeleide van de hyperbolische boogcosinus van een functie gelijk aan het quotiënt van de afgeleide van die functie gedeeld door de vierkantswortel van die functie in het kwadraat min één.

f(x)=\text{arccosh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{u^2-1}}

De tweede formule omvat de kettingregel en kan daarom worden gebruikt om elke hyperbolische arccosinus af te leiden. Als we x vervangen door de u, krijgen we in feite de eerste formule. In plaats daarvan werkt de eerste formule alleen voor de hyperbolische arccosinusderivaat van x.

afgeleide van de hyperbolische boogcosinus

Hyperbolische arccosinus is de inverse functie van hyperbolische cosinus, en daarom zijn de twee functies gerelateerd. U kunt de formule voor de afgeleide van deze trigonometrische functie bekijken door hier te klikken:

➤ Zie: formule voor de afgeleide van de hyperbolische cosinus

Voorbeelden van het hyperbolische arcsinusderivaat

voorbeeld 1

f(x)=\text{arccosh}(5x)

Om de afgeleide van de hyperbolische arccosinus te vinden, moeten we de overeenkomstige formule gebruiken, namelijk:

f(x)=\text{arccosh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{u^2-1}}

Daarom moeten we in de teller van de breuk de afgeleide van 5x plaatsen, wat 5 is. En in de noemer hoeven we alleen maar de vierkantswortel van de argumentfunctie in het kwadraat min 1 te plaatsen:

f(x)=\text{arccosh}(5x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{5}{\sqrt{(5x)^2-1}}=\cfrac{5}{\sqrt{25x^2-1}}

Voorbeeld 2

f(x)=\text{arccosh}(x^4-5x^2)

De uit deze oefening af te leiden functie is een hyperbolische arccosinus, dus gebruiken we de volgende formule om deze af te leiden:

f(x)=\text{arccosh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{u^2-1}}

Dus schrijven we in de teller de afgeleide van het argument van de functie en in de noemer de vierkantswortel van de functie van het argument verhoogd tot 2 min 1:

f(x)=\text{arccosh}(x^4-5x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{4x^3-10x}{\sqrt{\left(x^4-5x^2\right)^2-1}}

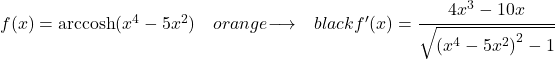
Bewijs van de afgeleide van de hyperbolische boogcosinus

Ten slotte zullen we de formule demonstreren voor de afgeleide van de hyperbolische boogcosinus.

y=\text{arccosh}(x)

Eerst transformeren we de hyperbolische boogcosinus in een hyperbolische cosinus:

x=\text{cosh}(y)

Van beide kanten van de gelijkheid leiden we het volgende af:

1=\text{senh}(y)\cdot y'

Wij zuiveren u:

y'=\cfrac{1}{\text{senh}(y)}

We gebruiken nu de trigonometrische identiteit die de hyperbolische sinus en de hyperbolische cosinus met elkaar in verband brengt om de noemer te wijzigen:

\text{cosh}^2(y)-\text{senh}^2(y)=1 \ \longrightarrow \ \text{senh}(y)=\sqrt{\text{cosh}^2(y)-1}

y'=\cfrac{1}{\sqrt{\text{cosh}^2(y)-1}}

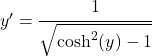
Maar eerst hebben we afgeleid dat x equivalent is aan de hyperbolische cosinus van y, dus de vergelijking blijft:

y'=\cfrac{1}{\sqrt{x^2-1}}

Gelijkwaardige producten

Laat een reactie achter

Je e-mailadres wordt niet gepubliceerd. Vereiste velden zijn gemarkeerd met *

Scroll naar boven