Het is heel gebruikelijk om functies weer te geven om de relatie tussen de verschillende variabelen waaruit deze functie bestaat grafisch te kunnen analyseren. Of soms worden dit soort representaties zelfs gebruikt om meerdere functies aan te schaffen. Dit wordt vooral gebruikt bij het uitvoeren van statistische onderzoeken. Dat gezegd hebbende, gaan we je vandaag een heel eenvoudige methode uitleggen die slechts uit 3 stappen bestaat om elke functie in een grafiek te kunnen zetten. Daarnaast bespreken we ook hoe we het grafische resultaat kunnen analyseren om conclusies te trekken.
Soorten functies
Ten eerste moeten we de kenmerken van verschillende soorten functies begrijpen en met welke verschillen rekening moet worden gehouden bij de representatie ervan. Op deze manier zal het voor ons gemakkelijker zijn om de grafische weergave uit te voeren, daarom zullen we nu kort commentaar geven op elk type. Het is de moeite waard om op te merken dat er veel soorten functies zijn, dus we zullen ons concentreren op de twee belangrijkste soorten polynomiale functies en stuksgewijs functies.
lineaire functies
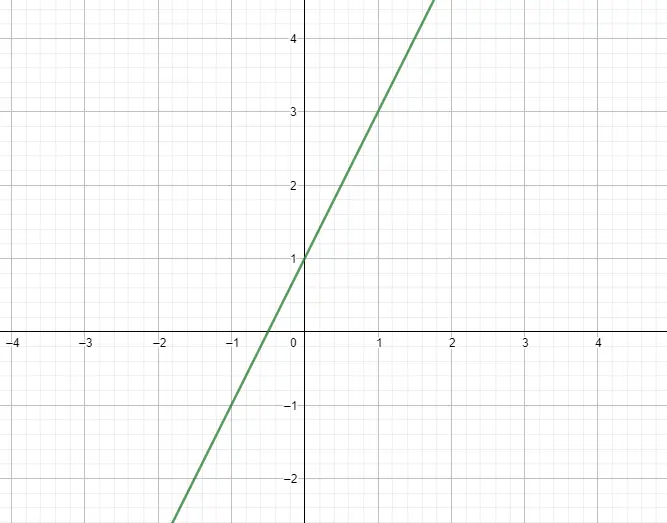
De lineaire functie of polynoomfunctie van de eerste graad is de functie waarvan de uitdrukking een polynoom van graad 1 is. Vervolgens volgt de uitdrukking ervan het model f(x) = mx + n , waarbij m de helling is en n de ordinaat. In principe hebben deze functies een grafische vorm die equivalent is aan een lijn. Hieronder ziet u een voorbeeld:
kwadratische functies
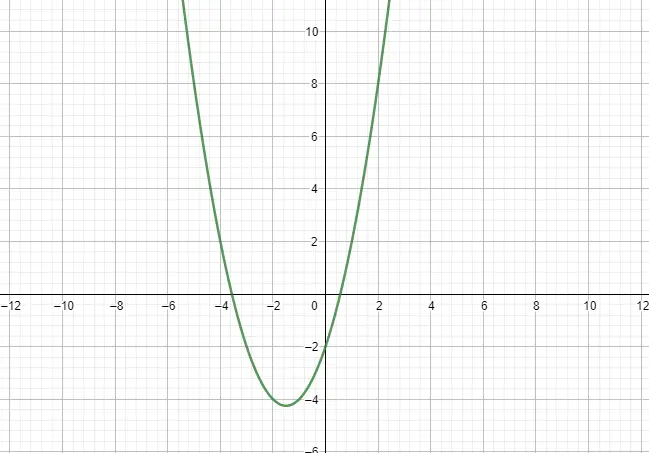
De kwadratische functie of parabolische functie wordt uitgedrukt door middel van een tweedegraads polynoom en heeft daarom een parabolische vorm. Als model dat we moeten volgen, zullen we rekening houden met de volgende uitdrukking: f(x) = ax² + bx + c, waarbij a ≠ 0. Er zijn ook twee andere opmerkelijke kenmerken van deze functies: amplitude en groei. Hieronder ziet u een voorbeeld:
Stuksgewijze functies
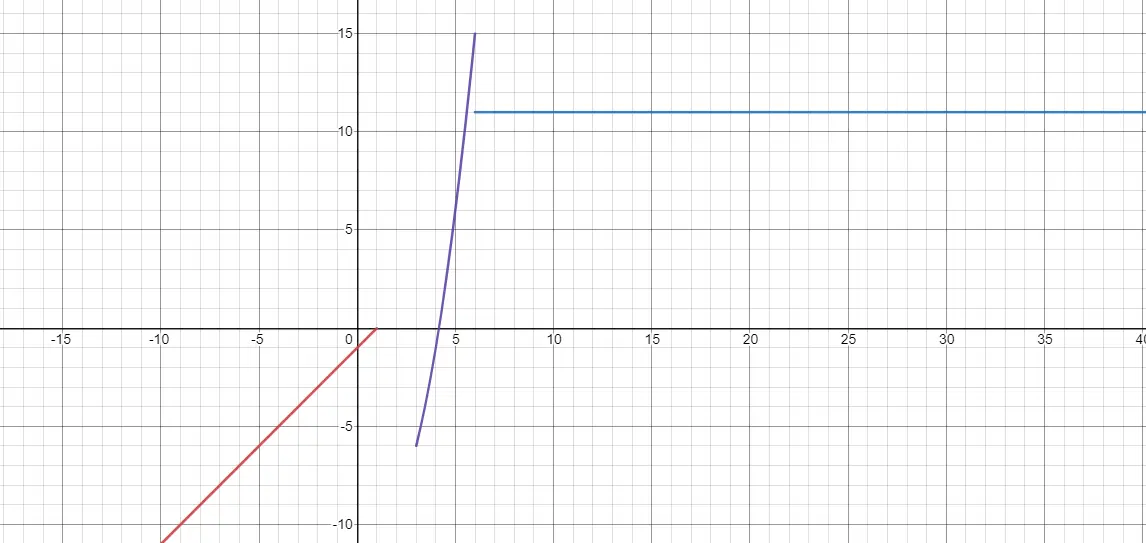
Een stuksgewijs gedefinieerde functie is een functie die verschillende definities heeft, afhankelijk van de waarde van x. Dus als x een bepaald waardenbereik in beslag neemt, moeten we een expressie proberen. Terwijl wanneer de x andere waarden inneemt, een andere expressie moet worden verwerkt. Het is hier dat we discontinuïteiten en dus grenzen vinden. Want waar de ene functie eindigt, kan een andere beginnen, maar zonder directe verbinding. Hieronder zie je een voorbeeld:
Hoe lineaire functies weergeven?
Om een lineaire functie te tekenen, moeten we drie zeer eenvoudige stappen volgen. Vervolgens zullen we de procedure uitleggen, maar als u wilt leren hoe u parabolische functies kunt tekenen, raden we u aan het volgende gedeelte te raadplegen.
Maak een tabel met waarden
Om een functie grafisch te kunnen weergeven, moeten we een waardentabel maken waarin we alle waarden van de variabelen schrijven. In principe zal dit ons in staat stellen een relatie tussen de twee variabelen tot stand te brengen en op deze manier het pad van de functie te volgen. Als u niet weet hoe u een waardentabel moet maken, kunt u deze laatste link bekijken. Hoewel het, samengevat, bestaat uit het geven van een waarde aan de onafhankelijke variabele en het vervangen van het onbekende in de functie die daarop betrekking heeft. We hebben dus de twee bijbehorende nummers. De volgende tabel toont een voorbeeld:
Uit de functie f(x) = 2x+1:
| X | f(x) |
| 0 | 1 |
| 1 | 3 |
| 2 | 5 |
| 3 | 7 |
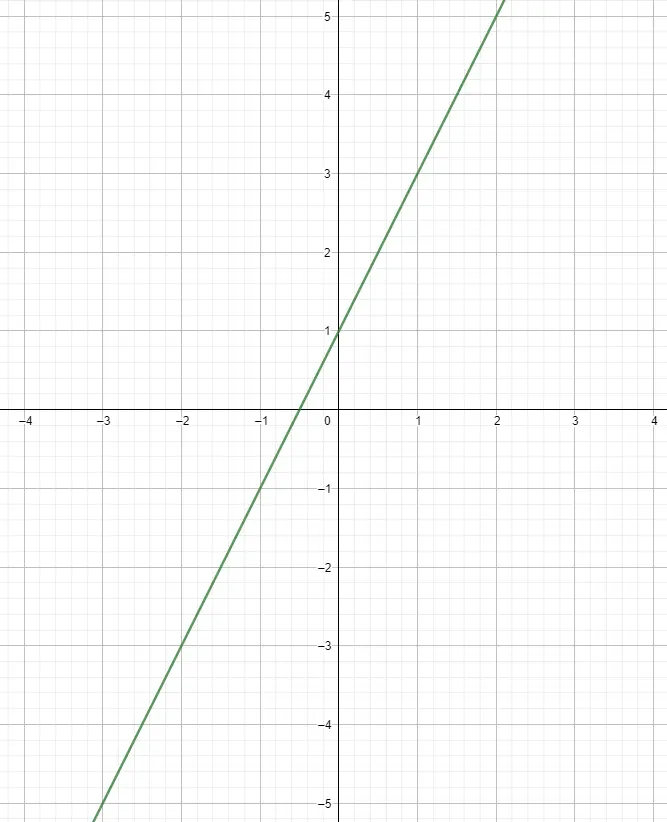
Teken punten in de grafiek en verbind ze door de functie te tekenen
Zodra we de tabel hebben gemaakt, kunnen we beginnen met het tekenen van de punten in een grafiek. We doen dit door de onafhankelijke variabele te associëren met de x-as en de andere met de y-as, en op deze manier verkrijgen we de punten. Je kunt zoveel punten tekenen als je wilt, maar om functies van deze stijl weer te geven is het meestal voldoende om vijf punten te berekenen. Sindsdien hebben ze een recht pad gevolgd en daarom blijft het hetzelfde, hoe ver je ook vordert.
Helling gebruiken om een lineaire functie te tekenen
Er is een tweede methode om lineaire functies grafisch weer te geven zonder waardentabellen, die bestaat uit het berekenen van de helling van de functie: m = (verticale variatie / horizontale variatie). Dus zodra we de helling hebben berekend, moeten we naar het startpunt kijken. Terugkerend naar het vorige voorbeeld f(x) = 2x+1, weten we dat het startpunt (0, 1) zal zijn, omdat bij x = 0 de computer = 1 (we leiden dit af uit de +1 in de uitdrukking) . En voeg dan gewoon de helling toe, die in dit geval gelijk is aan +2 verticaal voor 1 horizontaal. Dan weten we dat het volgende punt (1,3) zal zijn.
Hoe kwadratische functies weergeven?
Om een kwadratische functie weer te geven, kunnen we twee methoden volgen. De eerste omvat tabellen met waarden. En de tweede bestaat uit het berekenen van een reeks sleutelpunten: het hoekpunt, de snijpunten met de X-as en het snijpunt met de Y-as. Dit laatste is degene die we hieronder zullen uitleggen:
Bereken het hoekpunt van een parabool
Er zijn twee formules waarmee we het hoekpunt van een parabolische functie kunnen berekenen. In principe geeft de ene ons het hoekpunt van de X-as en de andere geeft ons het hoekpunt van de Y-as. Beide formules vind je hieronder, maar beide hebben een vergelijkbare structuur.
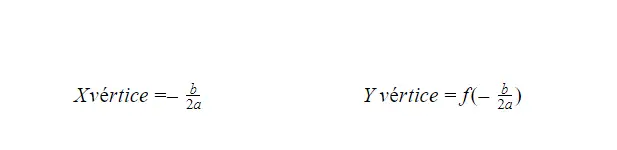
Bereken de snijpunten met de X-as van een kwadratische functie
Om de snijpunten van de te verkrijgen, hoeven we alleen maar de vergelijking op te lossen en hebben we al de waarden van X waarnaar we op zoek zijn. Het is vermeldenswaard dat we, omdat we een kwadratische functie zijn, twee resultaten krijgen, en niet slechts één.
Bereken het snijpunt met de Y-as van een kwadratische functie
Om tenslotte het snijpunt met de Y-as te verkrijgen, berekent u eenvoudigweg c = f(0). En aangezien een parabool altijd de verticale as (coördinaten) snijdt wanneer x = 0, zullen we zeggen dat het snijpunt van de Y-as (0,c) zal zijn. Zodra we al deze punten hebben, kunnen we ze in de grafiek tekenen en hoeven we ze alleen maar samen te voegen door de parabool zo te tekenen.
Hoe functies stuk voor stuk weergeven?
Om functies in stukjes te kunnen weergeven, kun je alle methoden combineren die we eerder hebben uitgelegd. Omdat functies van deze stijl zijn samengesteld uit alle soorten functies waar we het over hadden. Daarom zullen er enkele zijn die je moet berekenen via een waardentabel, en andere die je met andere methoden zult moeten berekenen. Zodra u echter de functies beheerst die we in dit artikel hebben uitgelegd, zult u geen problemen meer ondervinden bij het weergeven van functies in stukken.
Aan de andere kant, aangezien u bij het vertegenwoordigen van hen een continuïteitsonderzoek moet doen, raden wij u aan te leren hoe u de grenzen kunt oplossen , als u dat nog niet weet. Dit zal u helpen de eindpunten van elke functie correct weer te geven. Dat gezegd hebbende, bent u nu klaar om stuksgewijs functies en elk ander type functie in een grafiek te zetten. We geven u nu een reeks grafische tips en een zeer nuttige uitleg over de mogelijkheid van de rekenmachine om grafieken te maken.
Hoe maak je grafieken met de rekenmachine?
Als u een grafische rekenmachine heeft, kan deze ook grafieken maken. Dat kan heel gemakkelijk zijn als u de procedure eenmaal kent, maar als u nog steeds niet weet hoe u het moet doen, gaan we het u nu uitleggen.
- Toegang tot de grafische modus: de eerste stap is toegang krijgen tot de grafische of grafische weergaveoptie vanuit het menu. Deze optie kan een andere naam voor uw rekenmachine hebben, maar bevat woorden die lijken op grafieken of de woorden waar we het al over hebben gehad.
- Pas de grafiekopties aan: zodra we in de grafiekeditor zijn, moeten we een naam aan het bestand geven, de assen een label geven, het aantal elementen selecteren dat in een grafiek zal worden weergegeven en de esthetische opties van de weergave configureren. Dit is een zeer snelle stap om te doen.
- Voeg de punten van de functie toe: u kunt dan beginnen met het toevoegen van de punten die de figuur zullen vormen. U kunt dit doen door de punten met de volgende notatie te schrijven: (0,1), (3,2)… En u gaat door met het optellen van de punten totdat u klaar bent met het tekenen van de grafiek.
- Gebruik de functie “Preview”: zodra u het project hebt voltooid, kunt u een voorbeeld van het resultaat bekijken en zien of het wordt zoals verwacht. Bovendien beschikken veel sjablonen over bewerkingsopties met dit voorbeeld, zodat u het resultaat kunt aanpassen totdat het perfect is.
- Sla het project op: zodra de gehele bewerkingsprocedure is voltooid, vergeet dan niet om het op een gemakkelijk te onthouden locatie op te slaan. Op deze manier kunt u, wanneer u maar wilt, opnieuw toegang krijgen tot het project om het te bekijken of de gewenste verbeteringen aan te brengen.
Beste rekenmachines voor het weergeven van functies
Als u geïnteresseerd bent in de aanschaf van een grafisch model om functies op dezelfde rekenmachine te kunnen weergeven, raden wij twee modellen aan: de HP 50G en de HP Prime . Dit zijn twee modellen van de hoogste kwaliteit, ook al zijn ze duur, dus je moet jezelf afvragen of de investering het voor jou waard is. Als je bijvoorbeeld een carrière als techniek gaat studeren, die erg complex is in termen van wiskunde, dan wordt het ten zeerste aanbevolen om een van deze twee modellen aan te schaffen. Maar als je niet zoveel reken- of grafische kracht nodig hebt, is de Casio FX-9750GII misschien genoeg voor je.
Hoe functies online grafisch weergeven?
U kunt altijd kiezen voor de optie om online grafische programma’s te gebruiken, zoals: Desmos , Geogebra en vele andere. Op deze manier krijgt u op een snelle manier zeer nauwkeurige grafieken. We kunnen zeggen dat de getalvorm wordt gebruikt als je functies eenvoudig en snel in een grafiek wilt weergeven. Aan de andere kant, als je functies grafisch wilt weergeven zodat je ze kunt bewerken (al hun attributen kunt wijzigen) en hoogwaardige bronnen voor functieanalyse binnen handbereik hebt, dan raden we je aan een wetenschappelijke rekenmachine aan te schaffen.