Op deze pagina vindt u de meest gedetailleerde uitleg van de helling van een lijn: wat is de formule, rekenvoorbeelden, wat het concept van de helling van een lijn betekent,… U zult ook kunnen zien hoe u de helling gemakkelijk kunt identificeren van een lijn uit de vergelijking en bovendien kun je oefenen met oefeningen die stap voor stap worden opgelost.
Formule voor de helling van een lijn
De helling van een lijn is gelijk aan de verticale verplaatsing tussen twee punten gedeeld door de horizontale verplaatsing tussen dezelfde twee punten.
Dat wil zeggen, gegeven twee punten op een lijn:
![]()
De formule voor de helling van een lijn is:
![]()
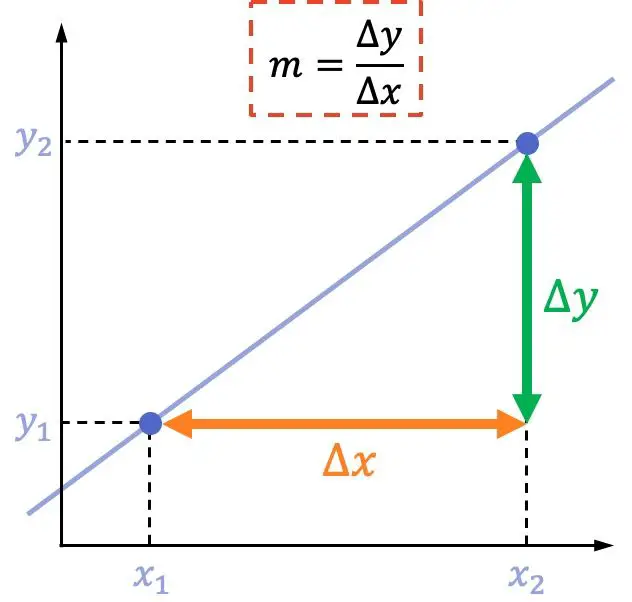
Voorbeeld van het berekenen van de helling van een lijn vanuit twee punten
Vervolgens zullen we een voorbeeld zien van hoe de helling van een lijn wordt berekend met de formule:
- Bereken de helling van de lijn die door de volgende twee punten gaat:
![]()
Om de helling van deze lijn te vinden, past u eenvoudigweg de formule toe:
![]()
De helling van de lijn is dus gelijk aan 3.
De helling van een lijn vinden op basis van zijn vergelijking
In het bovenstaande gedeelte hebben we zojuist gezien hoe je de helling van een lijn numeriek kunt bepalen. Het is echter niet altijd nodig om berekeningen uit te voeren, maar de waarde ervan kan ook worden afgeleid uit de vergelijking van een lijn. Elk type vergelijking is anders, dus we zullen elk geval afzonderlijk analyseren.
Helling gegeven de expliciete vergelijking van de lijn
De expliciete vergelijking van de lijn volgt de volgende uitdrukking:
![]()
Dan de parameter
![]()
komt overeen met de helling van de lijn.
Helling gegeven de punt-hellingsvergelijking van de lijn
De formule voor de punt-hellingvergelijking van de lijn is als volgt:
![]()
Zoals voorheen, de coëfficiënt
![]()
komt overeen met de helling van de lijn.
Helling gegeven de impliciete vergelijking van de lijn
Gegeven de impliciete vergelijking van de lijn (ook wel de algemene of cartesiaanse vergelijking genoemd):
![]()
De helling van de lijn kun je vinden door:
![]()
Helling waarbij rekening wordt gehouden met de richtingsvector van de lijn
De richtingsvector van de lijn is de vector die de richting aangeeft. Dus als de richtingsvector van een lijn is:
![]()
De helling van deze lijn is:
![]()
helling gegeven een hoek
Tenslotte, als een lijn een hoek vormt
![]()
op het positieve deel van de abscis-as (X-as) is de helling gelijk aan de raaklijn van de hoek:
![]()
Betekenis van de helling van een lijn
Met alle bovenstaande informatie weten we al heel goed hoe we de helling van een lijn kunnen vinden. Maar echt… wat betekent de helling van een lijn?
De helling van een lijn geeft de verticale eenheden aan waarmee de lijn stijgt voor elke horizontale eenheid van de grafiek.
In de weergave van de volgende lijn kunt u bijvoorbeeld zien dat deze voor elke horizontale eenheid 2 verticale eenheden vooruitgaat, omdat de helling gelijk is aan 2.

Bovendien geeft de helling van een lijn ook de steilheid aan:
- Als een lijn stijgend (stijgend) is, is de helling ervan positief.
- Als een lijn afneemt (aflopend), is de helling negatief.
- Als een lijn volledig horizontaal is, is de helling gelijk aan 0.
- Als een lijn volledig verticaal is, is de helling gelijk aan oneindig.


Relatieve positie van lijnen
Aan de andere kant kan de relatieve positie tussen twee lijnen ook bekend worden uit de eigenschappen van de hellingen:
- Als twee lijnen verschillende hellingen hebben, betekent dit dat ze elkaar snijden , dat wil zeggen dat ze elkaar in een punt snijden.
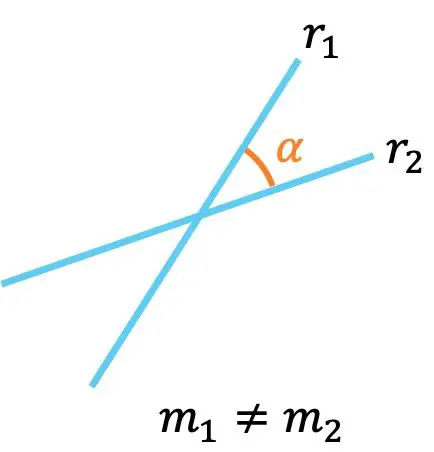
Bovendien kan de hoek tussen de twee lijnen over hun hellingen worden berekend met de volgende formule:
![]()
- Ten tweede, als twee lijnen dezelfde helling hebben, betekent dit dat ze evenwijdig zijn.

- Tenslotte voldoen de hellingen van twee loodrechte of orthogonale lijnen (die 90º vormen) aan de volgende voorwaarde:

Dit is een manier om erachter te komen of twee lijnen parallel of loodrecht op elkaar staan. Er zijn echter andere methoden en sommige zijn zelfs sneller. Voor meer informatie kun je naar de uitleg van loodrechtheid en parallelliteit tussen lijnen gaan. Bovendien leggen deze pagina’s ook uit hoe u een lijn kunt vinden die loodrecht (of evenwijdig) op een andere staat.
Problemen met de helling van een lijn opgelost
Oefening 1
Zoek de helling van de lijn die door de volgende twee punten gaat:
![]()
Om de helling van de lijn te berekenen, moet u de formule gebruiken:
![]()
Oefening 2
Bereken de helling van de lijn die door de volgende twee punten gaat:
![]()
Om de helling van de lijn te vinden, moet je de formule gebruiken:
![]()
Oefening 3
Wat is de helling van elke lijn?
![Rendered by QuickLaTeX.com \begin{array}{lll} A) \ y= 2x+3 & \qquad & B) \ y-3=4(x+1) \\[2ex] C) \ 6x+2y-7=0 & \qquad & D) \ \begin{cases}x=3-t \\[2ex] y=1+2t \end{cases} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5d405c8176957af59906c98149714570_l3.png)
A) De lijn wordt uitgedrukt als een impliciete vergelijking, dus de helling ervan is 2 (de term die bij de
![]()
).
B) De lijn wordt gedefinieerd door de punt-hellingsvergelijking, dus de helling is 4 (het getal vóór de haakjes).
C) De lijn heeft de vorm van een impliciete vergelijking, dus de helling is:
![]()
D) De lijn is gedefinieerd in de vorm van parametervergelijkingen, dus we moeten eerst de richtingsvector vinden en daarmee kunnen we de helling van de lijn berekenen. De componenten van de richtingsvector zijn dus de termen die bij de coëfficiënt horen
![]()
![]()
En zodra we de richtingsvector van de lijn kennen, kunnen we de helling van de lijn bepalen:
![]()
Oefening 4
Bepaal de helling van elke getekende lijn:

blauw rechts
De blauwe lijn wordt voor elke X met één Y verhoogd, dus de helling is gelijk aan 1.
![]()
rechts groen
De groene lijn wordt voor elke X met drie Y verhoogd, dus de helling is 3 .
![]()
rode lijn
De rode lijn neemt voor elke X af met twee Y, dus de helling is gelijk aan -2 .
![]()