▷ Gemiddelde en onmiddellijke veranderingssnelheid (opgeloste oefeningen)

Hier leggen we uit wat veranderingssnelheid, gemiddelde veranderingssnelheid en onmiddellijke veranderingssnelheid zijn. U zult verschillende voorbeelden zien van hoe u de veranderingssnelheid kunt berekenen en bovendien kunt u oefenen met opgeloste stapsgewijze oefeningen over de veranderingssnelheid.

Wat is de snelheid van verandering?

In de wiskunde is de veranderingssnelheid (TV) van een functie het verschil in de waarden van een functie op twee verschillende punten. Om de veranderingssnelheid tussen twee punten te berekenen, moeten daarom de waarden van de functie op deze twee punten worden afgetrokken.

$\text{TV}[a,b]=f(b)-f(a)$

Als twee afbeeldingen van een functie bijvoorbeeld f(2)=1 en f(5)=7 zijn, is hun veranderingssnelheid:

$\text{TV}[2,5]=f(5)-f(2)=7-1=6$

We hebben zojuist de wiskundige betekenis van veranderingssnelheid gezien, maar in de economie betekent het concept van veranderingssnelheid het volgende:

In de economie is de veranderingssnelheid tussen twee waarden het verschil daartussen, uitgedrukt als een percentage, dat wil zeggen dat de veranderingssnelheid van een variabele tussen verschillende perioden de relatieve verandering is. Om de veranderingssnelheid te berekenen, worden daarom de waarden van de twee verschillende perioden afgetrokken en wordt het verkregen resultaat gedeeld door de waarde van de initiële periode.

$\text{TV}[t,t+n]=\cfrac{Y_{t+n}-Y_t}{Y_t}\cdot 100$

Als de waarde van bepaalde aandelen bijvoorbeeld in één maand stijgt van € 35 naar € 50, zal het veranderingspercentage als volgt zijn:

$\text{TV}[t,t+1]=\cfrac{50-35}{35}\cdot 100=42,86 \ \%$

Gezien de twee mogelijke betekenissen van veranderingssnelheid, zullen we ons in dit artikel concentreren op het begrijpen van de wiskundige definitie van veranderingssnelheid. Er kunnen twee soorten veranderingssnelheden worden onderscheiden: de gemiddelde veranderingssnelheid en de onmiddellijke veranderingssnelheid. Hieronder vindt u de uitleg van elk type.

Gemiddeld veranderingspercentage

De gemiddelde veranderingssnelheid (TVM) van een functie in een interval is het aantal eenheden waarmee de functie toeneemt (of afneemt) voor elke eenheid waarmee de onafhankelijke variabele toeneemt. Daarom wordt de gemiddelde veranderingssnelheid van een functie berekend door de groei van de functie in een interval te delen door de amplitude van datzelfde interval.

$\text{TVM}[a,b]=\cfrac{f(b)-f(a)}{b-a}$

Om u te laten zien hoe het gemiddelde veranderingspercentage wordt berekend, hebben we hieronder stap voor stap een voorbeeld opgelost.

Voorbeeld van het berekenen van de gemiddelde veranderingssnelheid van een functie

Bereken de gemiddelde veranderingssnelheid in het interval [2,5] van de volgende functie:

$f(x) = x^2-1$

Eerst berekenen we de waarde van de functie op x=2 en x=5:

$f(5)= 5^2-1=25-1=24$

$f(2)=2^2-1=4-1=3$

En dan berekenen we de gemiddelde veranderingssnelheid van de functie in het interval door simpelweg de formule toe te passen:

$\text{TVM} [a,b] = \cfrac{f(b)-f(a)}{b-a}$

$\text{TVM} [2,5]=\cfrac{f(5)-f(2)}{5-2} = \cfrac{24 - 3}{5-2} = \cfrac{21}{3} = \bm{7}$

Omdat het resultaat van TVM[2,5] positief is, betekent dit dat de functie groeit in het interval [2,5]. Als het resultaat daarentegen negatief was geweest, zou dit betekenen dat de functie in dit interval afneemt.

Geometrische interpretatie van de gemiddelde veranderingssnelheid

Geometrisch gezien vertegenwoordigt de gemiddelde veranderingssnelheid van een functie in een interval de helling van de lijn die de uiterste punten van het interval verbindt.

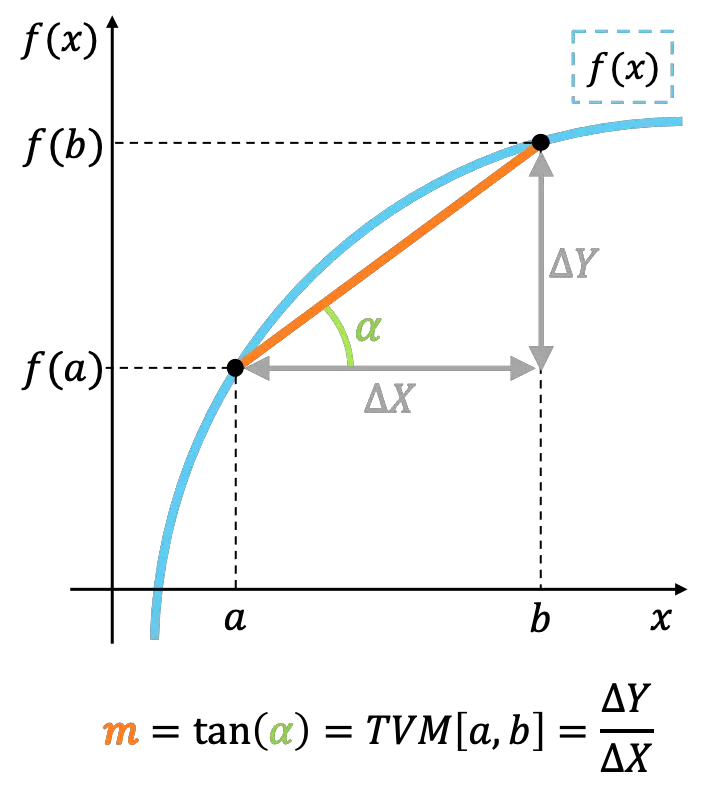
Momentane veranderingssnelheid

De momentane veranderingssnelheid (TVI) van een functie op een punt is de oneindig kleine limiet van de relatieve toename van de functie over een interval. Daarom wordt de momentane veranderingssnelheid berekend door de limiet van het quotiënt van f(a+h)-f(a) op te lossen met h dichter bij nul.

$\displaystyle\text{TVI}(a)=\lim_{h \to 0}\frac{f(a+h)-f(a)}{h}$

De waarde van de momentane veranderingssnelheid kan positief, negatief of nul zijn, en betekent dat de functie op dat punt respectievelijk toeneemt, afneemt of hetzelfde blijft.

Voorbeeld van het berekenen van de momentane veranderingssnelheid van een functie

Bereken de momentane veranderingssnelheid op het punt x=2 van de volgende functie:

$f(x) = x^2$

Om de momentane veranderingssnelheid te berekenen, moeten we de formule toepassen:

$\text{TVI} (a) = \lim\limits_{h \to 0} \cfrac{f(a+h)-f(a)}{h}$

$\text{TVI} (2) = \lim\limits_{h \to 0} \cfrac{f(2+h)-f(2)}{h} = \lim\limits_{h \to 0} \cfrac{(2+h)^2-2^2}{h}$

We lossen de opmerkelijke identiteit op:

$\lim\limits_{h \to 0} \cfrac{2^2+h^2+2\cdot 2 \cdot h -2^2}{h} = \lim\limits_{h \to 0} \cfrac{4+h^2+4h -4}{h} = \lim\limits_{h \to 0} \cfrac{h^2+4h}{h}$

➤ Als u de formules voor opmerkelijke identiteiten niet meer herinnert, vindt u alle formules op onze site gespecialiseerd in polynomen: www.polinomios.org

Laten we nu proberen de limiet op te lossen:

$\lim\limits_{h \to 0} \cfrac{h^2+4h}{h} = \cfrac{0^2+4\cdot 0}{0} =\cfrac{0}{0}$

Maar we vinden nul onbepaaldheid tussen nul, daarom:

$\lim\limits_{h \to 0} \cfrac{h^2+4h}{h}= \lim\limits_{h \to 0} \cfrac{\cancel{h}(h+4)}{\cancel{h}} = \lim\limits_{h \to 0} (h+4)$

➤ Zie: hoe je een limiet oplost met nul onbepaaldheid tussen nul

En tenslotte lossen we de limiet op:

$\lim\limits_{h \to 0} (h+4) = 0 +4 = \bm{4}$

Nog:

$\mathbf{TVI} \bm{(2) = 4}$

Omdat het resultaat van TVI(2) positief is, betekent dit dat de functie toeneemt bij x=2. Als het resultaat daarentegen negatief was geweest, zou dit betekenen dat de functie in dit stadium afneemt.

Geometrische interpretatie van de onmiddellijke veranderingssnelheid

Geometrisch gezien vertegenwoordigt de momentane veranderingssnelheid van een functie op een punt de helling van de lijn die de functie op datzelfde punt raakt.

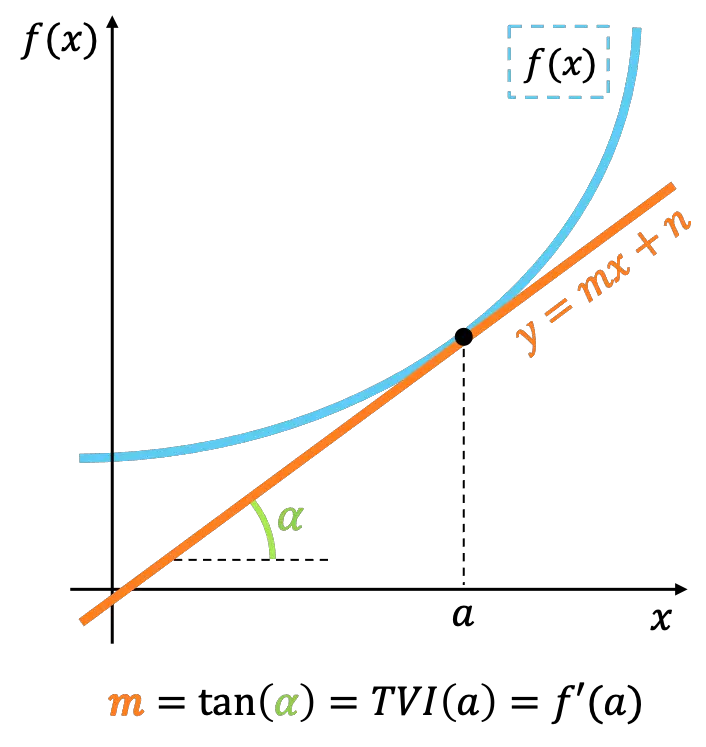
Als je goed kijkt, is de betekenis van onmiddellijke veranderingssnelheid gelijk aan het concept van een afgeleide van een functie . De momentane veranderingssnelheid wordt dus ook gebruikt om de waarde van de afgeleide van een functie op een punt te berekenen.

Opgeloste oefeningen over de mate van verandering

Oefening 1

Bereken de waarde van de veranderingssnelheid van de volgende functie in het interval [1,3].

$f(x)=x^2-5$

Zie de oplossing

Eerst bepalen we de waarde van de functie aan de uiteinden van het interval:

$f(1)=1^2-5=1-5=-4$

$f(3)=3^2-5=9-5=4$

En nu passen we de formule voor het veranderingspercentage toe:

$\text{TV}[a,b]=f(b)-f(a)$

$\text{TV}[1,3]=f(3)-f(1)=4-(-4)=4+4=\bm{8}$

Oefening 2

Bereken de gemiddelde veranderingssnelheid (TVM) van de volgende functie over het interval [1,4]:

$f(x)=2x+1$

Zie de oplossing

We berekenen eerst de afbeeldingen van de functie op x=1 en x=4.

$f(4)=2\cdot4+1=9$

$f(1)=2\cdot 1+1=3$

En we passen de formule toe voor het gemiddelde veranderingspercentage:

$\text{TVM} [a,b] = \cfrac{f(b)-f(a)}{b-a}$

$\text{TVM} [1,4] = \cfrac{f(4)-f(1)}{4-1} = \cfrac{9-3}{4-1}=\cfrac{6}{3} = \bm{2}$

Oefening 3

Zoek de gemiddelde veranderingssnelheid van de volgende functie in het interval [-1,3]:

$f(x)=(x+1)^2$

Zie de oplossing

Om de gemiddelde veranderingssnelheid te bepalen, moeten we eerst f(-1) en f(3) berekenen:

$f(3)=(3+1)^2=(4)^2=16$

$f(-1)=((-1)+1)^2=(0)^2=0$

We gebruiken nu de formule voor de gemiddelde veranderingssnelheid:

$\text{TVM} [a,b] = \cfrac{f(b)-f(a)}{b-a}$

$\text{TVM} [-1,3] = \cfrac{f(3)-f(-1)}{3-(-1)} = \cfrac{16-0}{3+1}=\cfrac{16}{4} = \bm{4}$

Oefening 4

Bereken de gemiddelde veranderingssnelheid in het interval [2,4] van de functie weergegeven in de volgende grafiek:

Zie de oplossing

We passen de formule toe voor het gemiddelde veranderingspercentage:

$\text{TVM} [a,b] = \cfrac{f(b)-f(a)}{b-a}$

$\text{TVM} [2,4]=\cfrac{f(4)-f(2)}{4-2}$

Zoals we in de formule zien, moeten we de waarde van f(4) en f(2) vinden. En dit kan eenvoudig worden gedaan door naar de grafische weergave van de functie te kijken:

$f(4)=5$

$f(2)=1$

En nu we de waarden van de functie kennen, vervangen we ze in de formule:

$\text{TVM}[2,4]=\cfrac{f(4)-f(2)}{4-2}=\cfrac{5-1}{4-2}=\cfrac{4}{2}=\bm{2}$

Oefening 5

Bereken de momentane veranderingssnelheid van de volgende functie op het punt x=2:

$f(x)=3x$

Zie de oplossing

Om de momentane veranderingssnelheid van de functie op het punt x = 2 te bepalen, passen we de overeenkomstige formule toe:

$\text{TVI}(a)=\lim\limits_{h \to 0} \cfrac{f(a+h)-f(a)}{h}$

$\begin{array}{l}\text{TVI}(2)=\lim\limits_{h \to 0} \cfrac{f(2+h)-f(2)}{h}=\\[4ex]=\lim\limits_{h \to 0} \cfrac{3(2+h)-3\cdot 2}{h} =\\[4ex]=\lim\limits_{h \to 0} \cfrac{6+3h-6}{h}= \lim\limits_{h \to 0} \cfrac{3h}{h} =\\[4ex]=\lim\limits_{h \to 0} \cfrac{3\cancel{h}}{\cancel{h}}=\lim\limits_{h \to 0} 3 = \bm{3}\end{array}$

Oefening 6

Bepaal de momentane veranderingssnelheid (TVI) van de volgende functie op het punt x=1:

$f(x)=x^2+1$

Zie de oplossing

We passen de formule toe voor de momentane veranderingssnelheid:

$\text{TVI} (a) = \lim\limits_{h \to 0} \cfrac{f(a+h)-f(a)}{h}$

$\text{TVI} (1) = \lim\limits_{h \to 0} \cfrac{f(1+h)-f(1)}{h}$

Vervolgens berekenen wij

$f(1+h)$

$f(1):$

$f(1+h) = (1+h)^2+1$

$f(1)=1^2+1=1+1=2$

En we vervangen de waarden gevonden in de limiet:

$\text{TVI} (1) = \lim\limits_{h \to 0} \cfrac{f(1+h)-f(1)}{h}= \lim\limits_{h \to 0} \cfrac{(1+h)^2+1-2}{h} =\lim\limits_{h \to 0} \cfrac{(1+h)^2-1}{h}$

We lossen het opmerkelijke product op:

$\lim\limits_{h \to 0} \cfrac{1^2+h^2+2\cdot 1 \cdot h-1}{h}=\lim\limits_{h \to 0} \cfrac{1+h^2+2h-1}{h}=\lim\limits_{h \to 0} \cfrac{h^2+2h}{h}$

Laten we nu proberen de limiet op te lossen:

$\lim\limits_{h \to 0} \cfrac{h^2+2h}{h}=\cfrac{0^2+2\cdot 0}{0} = \cfrac{0}{0}$

Maar we vinden de onbepaalde vorm nul gedeeld door nul, dus we ontbinden de polynoom van de teller van de breuk en vereenvoudigen:

$\lim\limits_{h \to 0} \cfrac{h^2+2h}{h}=\lim\limits_{h \to 0} \cfrac{h(h+2)}{h} = \lim\limits_{h \to 0} \cfrac{\cancel{h}(h+2)}{\cancel{h}}= \lim\limits_{h \to 0}(h+2)$

➤ Als je niet weet hoe je een nul-onbepaaldheid tussen nul moet oplossen , kun je de volledige uitleg in de bovenstaande link bekijken over hoe je een limiet met een nul-onbepaaldheid tussen nul kunt oplossen.

En ten slotte lossen we de limiet op:

$\lim\limits_{h \to 0}(h+2) = 0+2 =\bm{2}$

Samenvattend is de momentane veranderingssnelheid van de functie op het punt x = 1 gelijk aan 2.

$\mathbf{TVI} \bm{(1) = 2}$

Oefening 7

Zoek de momentane veranderingssnelheid van de volgende functie op het punt x = 2:

$f(x)=4x^2-x+3$

Zie de oplossing

We gebruiken eerst de formule voor de onmiddellijke veranderingssnelheid:

$\text{TVI} (a) = \lim\limits_{h \to 0} \cfrac{f(a+h)-f(a)}{h}$

$\text{TVI} (2) = \lim\limits_{h \to 0} \cfrac{f(2+h)-f(2)}{h}$

Wij berekenen

$f(2+h)$

$f(2):$

$f(2+h) = 4(2+h)^2-(2+h)+3=4(2+h)^2-h+1$

$f(2) =4\cdot 2^2-2+3=4\cdot 4-2+3 =17$

En we vervangen de waarden gevonden in de limiet:

$\text{TVI} (2) = \lim\limits_{h \to 0} \cfrac{f(2+h)-f(2)}{h}=\\[4ex]=\lim\limits_{h \to 0} \cfrac{4(2+h)^2-h+1-17}{h}=\\[4ex]= \lim\limits_{h \to 0} \cfrac{4(2+h)^2-h-16}{h}$

We berekenen de opmerkelijke gelijkheid:

$\lim\limits_{h \to 0} \cfrac{4(2^2+h^2+2\cdot 2 \cdot h)-h-16}{h}=\lim\limits_{h \to 0} \cfrac{4(4+h^2+4h)-h-16}{h}$

We werken met de teller:

$\lim\limits_{h \to 0} \cfrac{16+4h^2+16h-h-16}{h}=\lim\limits_{h \to 0} \cfrac{4h^2+15h}{h}$

Laten we nu proberen de limiet op te lossen:

$\lim\limits_{h \to 0} \cfrac{4h^2+15h}{h}=\cfrac{4\cdot0^2+15\cdot 0}{0} = \cfrac{0}{0}$

Maar we verkrijgen de onbepaaldheid nul gedeeld door nul, dus ontbinden we de polynomen in factoren en vereenvoudigen:

$\lim\limits_{h \to 0} \cfrac{4h^2+15h}{h}=\lim\limits_{h \to 0} \cfrac{h(4h+15)}{h}=\lim\limits_{h \to 0} \cfrac{\cancel{h}(4h+15)}{\cancel{h}}= \lim\limits_{h \to 0}(4h+15)$

En ten slotte lossen we de limiet op:

$\lim\limits_{h \to 0}(4h+15)=4\cdot 0+15 =\bm{15}$

Nog:

$\mathbf{TVI} \bm{(2) = 15}$

Wat is de snelheid van verandering?

Gemiddeld veranderingspercentage

Voorbeeld van het berekenen van de gemiddelde veranderingssnelheid van een functie

Geometrische interpretatie van de gemiddelde veranderingssnelheid

Momentane veranderingssnelheid

Voorbeeld van het berekenen van de momentane veranderingssnelheid van een functie

Geometrische interpretatie van de onmiddellijke veranderingssnelheid

Opgeloste oefeningen over de mate van verandering

Oefening 1

Oefening 2

Oefening 3

Oefening 4

Oefening 5

Oefening 6

Oefening 7

Laat een reactie achter Reactie annuleren