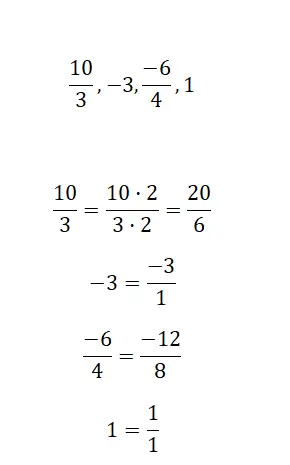Gelijkwaardige breuken

In dit artikel vindt u een uitleg over gelijkwaardige breuken of gelijke breuken die zeer compleet en gemakkelijk te begrijpen is. Meer specifiek zullen we het hebben over hun definitie, hoe je ze kunt berekenen en hoe je kunt weten of twee breuken gelijkwaardig zijn. Op deze manier weet je uiteindelijk alles wat je nodig hebt om oefeningen over gelijkwaardige breuken op te lossen, zoals degene die we je aan het einde zullen presenteren. Dat gezegd hebbende, laten we beginnen met het onderwerp.

Equivalente breukencalculator

Met behulp van deze equivalente breukencalculator kunt u controleren of twee breuken gelijk zijn, zonder dat u daarvoor berekeningen hoeft uit te voeren. De werking ervan is heel eenvoudig, in feite moet u de waarden invoeren die overeenkomen met de twee tellers en de twee noemers en op de knop “Berekenen” drukken.

A/B= /

C/D= /

resultaat =

Wat zijn gelijkwaardige breuken?

Equivalente breuken zijn breuken die dezelfde numerieke waarde uitdrukken . Daarom zijn het breuken die gelijkwaardig zijn aan hetzelfde resultaat, zelfs als ze een andere teller en noemer hebben. Dit betekent dat ze een proportionele relatie hebben, die van twee soorten kan zijn: versterkt of vereenvoudigd. Vervolgens laten we u een grafisch voorbeeld van equivalente breuken zien, zodat het concept beter wordt begrepen.

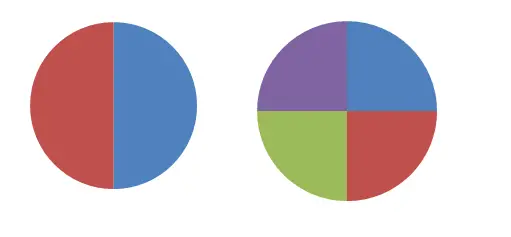
In de vorige afbeelding zie je twee cirkels verdeeld in twee en vier delen. Als we de eerste proberen te definiëren door een breuk, zullen we zeggen dat elk deel gelijk is aan 1/2 van het geheel, terwijl we in de tweede figuur de breuk 1/4 zullen gebruiken. Het is duidelijk dat deze twee breuken niet gelijkwaardig zijn , aangezien ze verschillende hoeveelheden vertegenwoordigen. Maar als we twee stukken van de tweede cirkel (2/4) nemen, is deze uitdrukking gelijk aan 1/2.

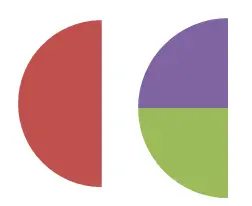
In deze tweede afbeelding ziet u de gelijkwaardigheid tussen 1/2 en 2/4 , deze kan ook numeriek worden geverifieerd. Omdat 1/2 = 0,5 en 2/4 = 0,5. Volgens de definitie waar we eerder commentaar op gaven, zijn de twee breuken gelijkwaardige breuken als ze dezelfde numerieke waarde uitdrukken.

Voorbeelden van gelijkwaardige breuken

We laten je nu 5 voorbeelden zien van gelijkwaardige breuken. En als je wilt begrijpen hoe we ze hebben berekend, raden we je aan verder te lezen.

• Breuken gelijk aan een helft: 2/4, 3/6, 4/8, enz.
• Breuken gelijk aan een terts: 2/6, 3/9, 4/12, etc.
• Breuken gelijk aan een kwart: 2/8, 3/12, 4/16, enz.
• Breuken gelijk aan eenheid: 4/4, 7/7, 15/15, enz.
• Breuken gelijk aan een kwint: 2/10, 3/15, 4/20, etc.

Hoe gelijkwaardige breuken berekenen?

Om gelijkwaardige breuken te krijgen, moeten we de teller en de noemer met hetzelfde getal vermenigvuldigen of delen . Omdat we, als we beide delen van de breuk op dezelfde manier wijzigen, een proportionele relatie behouden. Daarom kunnen we twee methoden gebruiken: versterking en reductie.

Het vinden van een equivalente fractie door amplificatie

In dit eerste geval moeten we een initiële breuk vermenigvuldigen met een bepaalde numerieke waarde. Dit betekent dat we de teller en de noemer met dit getal moeten vermenigvuldigen. Om je het met een voorbeeld te laten zien, laten we je hieronder twee gelijkwaardige breuken zien, die je bekomt na een vermenigvuldiging:

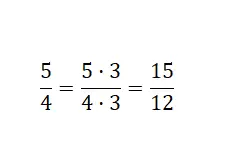
Wat we deden was beide delen van de breuk met drie vermenigvuldigen: 5 x 3 = 15 en 4 x 3 = 12 . We verkrijgen dus een versterkte equivalente fractie, omdat deze groter is. Concluderend hebben we een breuk gevonden die is samengesteld uit verschillende numerieke waarden, die dezelfde hoeveelheid uitdrukt als de oorspronkelijke breuk.

Het vinden van een equivalente breuk door vereenvoudiging

Ten tweede kunnen we ervoor kiezen een breuk te vereenvoudigen door de teller en de noemer van een gegeven breuk te delen. Op deze manier krijgen we nog een gelijkwaardige breuk , nog eenvoudiger dan de eerste. Het is echter de moeite waard te vermelden dat deze methode alleen werkt als de initiële uitdrukking geen onherleidbare breuk is, aangezien deze laatste niet verder kan worden gereduceerd. Hieronder ziet u een voorbeeld van het berekenen van een equivalente fractie door reductie (vereenvoudiging).

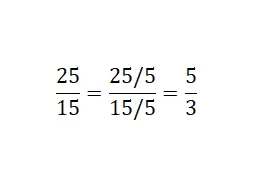
Zoals je op de afbeelding kunt zien, hebben we zowel de teller als de noemer van de breuk gedeeld door een gemeenschappelijke deler . In dit voorbeeld hebben we er vijf gebruikt: 25/5 = 5 en 15/5 = 3. Uiteindelijk hebben we de onherleidbare equivalente fractie van 25/15 verkregen.

Hoe weet je of twee breuken gelijkwaardig zijn?

Om equivalente breuken te identificeren, moeten we een van de drie procedures volgen die we hieronder zullen uitleggen. Opgemerkt moet worden dat de tweede verband houdt met de vereenvoudiging van breuken waar we het in de vorige sectie over hadden.

Tellers vermenigvuldigen met noemers

Als u de gelijkwaardigheid tussen twee breuken wilt controleren, kunt u deze eerste procedure gebruiken. Kortom, je moet de teller van de eerste breuk vermenigvuldigen met de noemer van de tweede. Vervolgens moet je de teller van de tweede breuk vermenigvuldigen met de noemer van de eerste. Als beide resultaten hetzelfde opleveren , zijn deze breuken gelijkwaardig. Kijk naar het volgende voorbeeld:

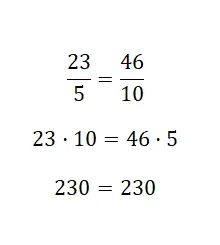
In dit laatste voorbeeld hebben we geverifieerd dat de twee breuken gelijkwaardig waren. Dit voorbeeld was gemakkelijk te zien, omdat de tweede breuk het dubbele is van de eerste, dat wil zeggen dat ze een versterkte equivalentierelatie hebben. Opgemerkt moet worden dat deze procedure redelijk comfortabel in gebruik is, het volstaat alleen om de kruisen te vermenigvuldigen. Maar we raden u ook aan om de andere twee systemen te leren gebruiken, omdat u hierdoor meer wiskundige hulpmiddelen tot uw beschikking krijgt.

Vereenvoudig breuken

Als het om niet-irreduceerbare breuken gaat, kunnen we deze andere methode gebruiken, die bestaat uit het zoveel mogelijk verkleinen van de breuk die uit de grootste getallen bestaat. Als we bij het maken van deze reductie ontdekken dat de kleinere fractie het onherleidbare is van de andere, dan kunnen we aannemen dat ze gelijkwaardig zijn.

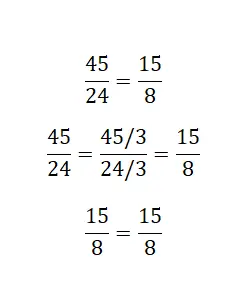
Oplossen en egaliseren van verdeeldheid

Ten slotte kun je je toevlucht nemen tot de quotiëntoplossing die door breuken wordt gegenereerd, omdat een gemengd getal altijd een deling is. Kortom, je moet de equivalente numerieke waarde van de twee breuken berekenen, en als het hetzelfde getal is, dan zijn ze gelijkwaardig. In de volgende afbeelding zie je een heel duidelijk voorbeeld:

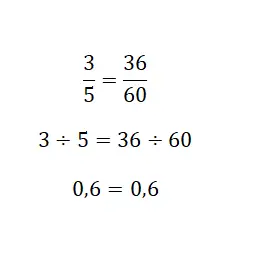
Oefeningen op gelijkwaardige breuken

Nu je de hele theorie hebt gelezen, kun je proberen de volgende oefeningen op te lossen, waardoor je de uitleg helemaal begrijpt. We raden u aan om ze zelf op te lossen en zodra u ze heeft, uw resultaat te vergelijken met het resultaat dat wij u aanbieden. Dat gezegd hebbende, laten we je oefenen:

Oefening 1

Vind een equivalente breuk door vereenvoudiging voor elke breuk die we aanbieden:

Om deze oefening op te lossen, past u eenvoudigweg de vereenvoudiging van breuken toe, waardoor u de equivalente onherleidbare breuk verkrijgt. De vier voorbeelden lijken erg op elkaar, dus er is niet veel moeite om ze op te lossen.

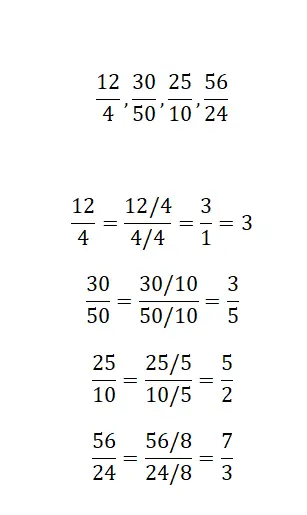
Oefening 2

Vind een equivalente fractie door versterking voor elke fractie die we voorstellen:

Vervolgens zul je de breuken die wij voorstellen moeten versterken, op deze manier krijg je grotere equivalente breuken. Het maakt niet uit welk getal je gebruikt om de vermenigvuldigingen uit te voeren, we doen het bijvoorbeeld met 2 en 3.

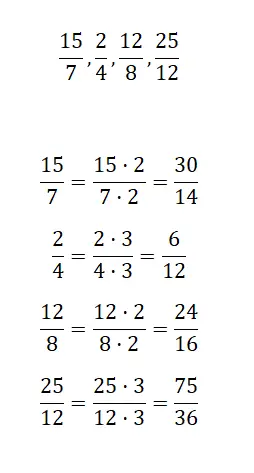
Oefening 3

Bepaal of de volgende breuken gelijkwaardig zijn:

Om erachter te komen of twee breuken gelijkwaardig zijn, moet je een van de drie methoden gebruiken die we hierboven hebben uitgelegd. U zult zien dat de oplossingen zijn opgelost met de eerste procedure, hoewel u vrij bent om het gewenste systeem te gebruiken.

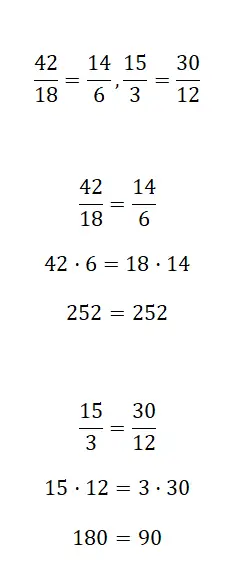
Oefening 4

Bereken de equivalente breuken van de volgende uitdrukkingen:

In deze laatste oefening zul je de uitdrukkingen die we voorstellen ( hele getallen en gemengde getallen) moeten herschrijven in breukvorm, in een poging een gelijkwaardigheidsrelatie te behouden.