Op deze pagina vindt u hoe u de afstand tussen twee punten in de geometrie kunt berekenen (formule). Ook krijg je voorbeelden te zien en daarnaast te oefenen met opgeloste oefeningen van de afstand tussen twee punten.
Wat is de formule voor de afstand tussen twee punten?
De afstand tussen twee punten is gelijk aan de lengte van het segment dat ze verbindt. Daarom moeten we in de wiskunde, om de afstand tussen twee verschillende punten te bepalen, de kwadraten van de verschillen tussen hun coördinaten berekenen en vervolgens de wortel vinden van de som van de genoemde kwadraten.
Met andere woorden, de formule die wordt gebruikt om de afstand tussen twee verschillende punten op het cartesiaanse vlak te berekenen is als volgt:
Beschouw de coördinaten van twee verschillende punten:
![]()
De formule voor de afstand tussen twee punten is:
![]()
Deze formule komt uit de grootte van een vector. Wat we met deze formule feitelijk doen, is het berekenen van de grootte van de vector die wordt bepaald door de twee punten in kwestie. Meer hierover lees je in de uitleg wat de modulus van een vector is .
Aan de andere kant kan in de analytische meetkunde de demonstratie van de formule voor de afstand tussen twee punten ook worden gedaan met behulp van de stelling van Pythagoras:
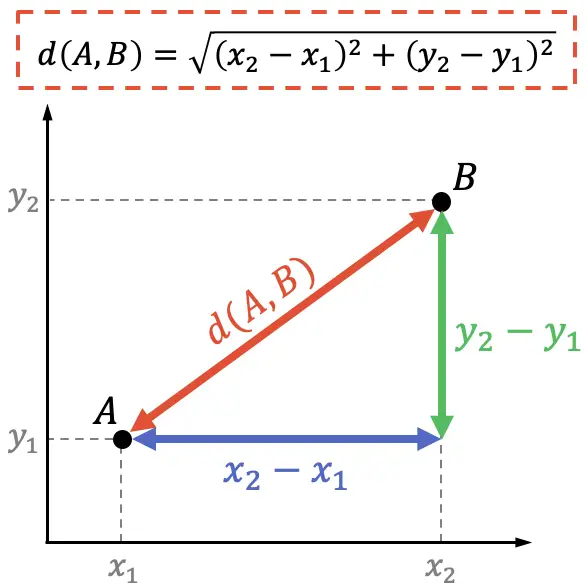
De stelling van Pythagoras stelt dat het kwadraat van de hypotenusa van een rechthoekige driehoek gelijk is aan de som van de kwadraten van zijn benen, daarom:
![]()
En om de formule te verkrijgen, hoeft u alleen maar de afstand tussen de 2 punten te vinden:
![]()
Ten slotte is het de moeite waard om op te merken dat, als we zouden werken met punten met 3 coördinaten, de formule voor de afstand tussen twee punten in de ruimte (in R3) hetzelfde zou zijn, maar met toevoeging van de Z-coördinaat:
![]()
Voorbeeld van het berekenen van de afstand tussen twee punten
Nadat we de definitie van de formule voor de afstand tussen twee punten hebben gezien, gaan we nu kijken hoe we deze afstand kunnen bepalen aan de hand van een voorbeeld:
- Bereken de afstand tussen de volgende twee punten:
![]()
Om de afstand tussen de twee punten geometrisch te vinden, past u eenvoudigweg de formule toe:
![]()
Nu vervangen we de coördinaten van de punten in de formule:
![]()
En wij doen de berekeningen:
![Rendered by QuickLaTeX.com \begin{aligned} d(A,B) &= \sqrt{(3+1)^2+(4-7)^2 \vphantom{\frac{1}{2}}} \\[2ex] &= \sqrt{4^2+(-3)^2 \vphantom{\frac{1}{2}}} \\[2ex] &= \sqrt{16+9}\\[2ex] &= \sqrt{25}\\[2ex] & = \bm{5}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4e48600907e65f89fb9be0d55a2d3b3a_l3.png)
De afstand tussen de twee punten is dus gelijk aan 5 eenheden.
Het is duidelijk dat de afstandswaarde ons altijd een positief teken moet geven, omdat afstanden altijd positief zijn. Anders betekent dit dat we een fout hebben gemaakt in een stap.
Problemen met de afstand tussen twee punten oplossen
Oefening 1
Bereken de afstand tussen de volgende twee punten:
![]()
Om de geometrische afstand tussen de twee punten te vinden, gebruikt u eenvoudigweg de formule:
![]()
Nu vervangen we de coördinaten van de punten in de formule:
![]()
En wij doen de berekeningen:
![Rendered by QuickLaTeX.com \begin{aligned} d(A,B) & = \sqrt{(-3)^2+3^2 } \\[2ex] & = \sqrt{9+9 } \\[2ex] & = \bm{\sqrt{18}} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-81d70676cabdc2985f2ebe7b88c54e2d_l3.png)
Oefening 2
Bereken de afstand tussen de volgende twee punten:
![]()
Om de wiskundige afstand tussen de twee punten te vinden, moeten we de bijbehorende formule gebruiken:
![]()
Nu vervangen we de coördinaten van de punten in de formule:
![]()
En wij doen de berekeningen:
![Rendered by QuickLaTeX.com \begin{aligned} d(A,B) &= \sqrt{(-12)^2+(-5)^2 } \\[2ex] &= \sqrt{144+25 }\\[2ex] &= \sqrt{169} \\[2ex] &= \bm{13}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1c9f9f5c93377868a352891d5b09630a_l3.png)
Oefening 3
Bereken de omtrek van de driehoek gevormd door de punten A, B en C, hieronder grafisch weergegeven:
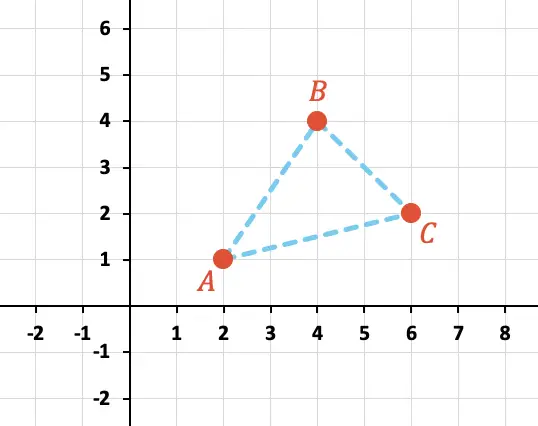
Eerst moeten we de X- en Y-coördinaten van elk punt in de grafiek identificeren:
![]()
![]()
![]()
En nu moeten we de afstand tussen alle punten berekenen met de formule:
![]()
![]()
![]()
De omtrek van de driehoek is dus de som van de lengte van de 3 zijden:
![]()
Oefening 4
Controleer of de driehoek waarvan de hoekpunten de punten A, B en C zijn, een gelijkbenige driehoek is. Maar de drie punten:
![]()
Wil een driehoek gelijkbenig zijn, dan moeten twee zijden gelijk zijn. We moeten daarom de lengte van elk van zijn zijden vinden, die overeenkomt met de afstanden tussen de hoekpunten.
We berekenen daarom de afstand tussen de hoekpunten van de driehoek:
![]()
![]()
![]()
Dus de driehoek heeft 2 identieke zijden en de derde zijde meet anders dan de andere twee, dan is het feitelijk een gelijkbenige driehoek.
Oefening 5
Zoek een punt op de Y-as dat op gelijke afstand ligt van de volgende twee punten:
![]()
Allereerst, als het punt zich op de computeras (OY-as) bevindt, betekent dit dat de abscis van het punt nul is:
![]()
Ten tweede, als het punt op gelijke afstand ligt van de punten A en B, betekent dit dat aan de volgende vergelijking wordt voldaan:
![]()
Met behulp van de formule voor de afstand tussen twee punten kunnen we dus de waarde van de variabele y uit de vorige vergelijking vinden:
![]()
Omdat beide kanten van de vergelijking een wortel hebben, kunnen we ze vereenvoudigen:
![]()
We lossen de opmerkelijke machten en gelijkheden (of opmerkelijke producten) op:
![]()
En we gaan door totdat we de waarde van de onbekende y vinden:
![]()
![]()
![]()
![]()
Kort gezegd is het punt dat de probleemstelling ons vroeg:
![]()
Als je dit artikel nuttig vond, ben je waarschijnlijk ook geïnteresseerd in oefeningen over de afstand tussen een punt en een lijn . Op de gelinkte pagina vind je niet alleen opgeloste oefeningen stap voor stap, maar ook een uitgebreide uitleg over het berekenen van de afstand tussen punten en lijnen, voorbeelden en toepassing van de formule voor de afstand tussen een punt en een lijn om een ander type afstand te bepalen .