Wat is polynomiale factoring? Het is een wiskundige techniek waarmee u een polynoom kunt ontleden in eenvoudiger factoren of uitdrukkingen. En dankzij deze vereenvoudiging zullen we bewerkingen tussen verschillende algebraïsche uitdrukkingen gemakkelijker en comfortabeler kunnen uitvoeren. Daarom zullen we in dit artikel verschillende methoden voor het factoriseren van polynomen en alle mogelijke gevallen van factorisatie bespreken.
Hoe ontbind je een polynoom in factoren?
Er zijn veel factorisatiemethoden die hun eigen oplossingsstructuur hebben, maar uiteindelijk op hetzelfde berusten. Daarnaast vindt u ook een grote verscheidenheid aan gevallen met betrekking tot de polynomiale configuratie. Daarom zullen we in de volgende paragrafen alle bestaande procedures bespreken en wanneer we deze moeten gebruiken. Ten slotte passen we het toe op een echt voorbeeld, zodat u de concepten helemaal onder de knie krijgt.
Factoreer een polynoom met de regel van Ruffini
De meest gebruikte methode voor het ontbinden van polynomen is de regel van Ruffini , omdat deze gemakkelijk te gebruiken is en het resultaat snel te vinden is. Het normale is om deze techniek te gebruiken om polynomen van graad groter dan twee te ontbinden, of soms zelfs om polynomen van de tweede graad te ontbinden. Omdat je hiermee de wortels van deze polynoom heel grafisch kunt bepalen . Hoewel dit gebruik zal worden uitgelegd in de volgende sectie, die zich richt op de wortels van een wiskundige uitdrukking van dit type.
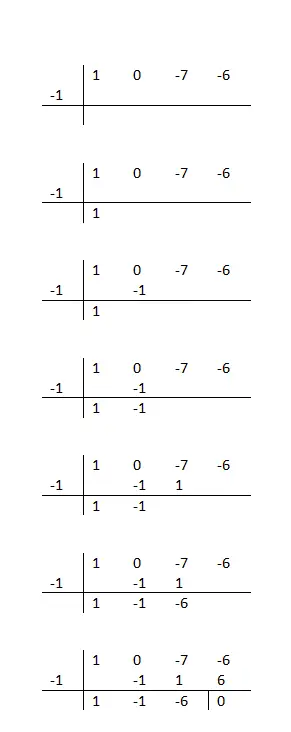
Hoe moet Ruffini polynomen ontbinden in factoren?
Kortom, we zullen de coëfficiënten van het deeltal in een horizontale lijn moeten schrijven en de waarde van een mogelijke wortel van het polynoom in de zijkant. We zeggen mogelijk, omdat we zullen moeten zoeken naar een deler waarmee we een rest gelijk aan nul kunnen verkrijgen. Anders is dit nummer geen geldige root en moet je het blijven proberen.
Als tip raden wij u aan alleen de delergetallen van de onafhankelijke term (laatste waarde van de horizontale lijn) te proberen. Om te weten of het door u gekozen getal juist is, hoeft u dus alleen maar de volgende reeks berekeningen te volgen:
Je verlaagt de coëfficiënt, vermenigvuldigt deze met de wortel die je test, schrijft deze onder de volgende coëfficiënt en voert verticale optelling uit. U hoeft deze stappen alleen maar tot het einde te herhalen, en als u klaar bent, weet u of deze waarde correct is of niet. Omdat alleen getallen die een rest van nul opleveren, geldig zijn.
Als de wiskundige procedure die u moet volgen niet erg duidelijk voor u is, kunt u het voorbeeld in de kolom links van deze tekst bekijken. We raden u ook aan te proberen de volgende polynoom in factoren te ontbinden: x³ + 2x² – x – 2 (gebaseerd op het voorbeeld). En tot slot, om te weten of je de oefening goed hebt opgelost of niet, kun je je resultaat met deze vergelijken:
- Excessieve uitdrukking = x² + 3x + 2
- rest = 0
We zullen nu een korte uitleg geven over de toepassing van Ruffini bij factorisatie . Maar als je in detail wilt weten hoe deze wiskundige hulpbron wordt gebruikt, raden we je aan het laatste artikel te raadplegen dat we hebben gelinkt, omdat alles daar heel goed wordt uitgelegd. Dat gezegd hebbende, laten we beginnen met uit te leggen hoe je polynomen kunt ontbinden met de regel van Ruffini:
- We tekenen het raster: zoals we in de afbeelding hierboven kunnen zien, maken we een doos waarin we de Ruffini gaan maken. Kortom, u moet de coëfficiënten van de uitdrukking horizontaal ordenen, zonder de waarden met een nulwaarde achter te laten. Uiteindelijk zou je een representatie moeten hebben die lijkt op die in de afbeelding, maar met de waarden van je polynoom.
- We berekenen de wortels: zodra we de structuur hebben getekend en er zeker van zijn dat alle getallen correct zijn geschreven, gaan we verder met het berekenen van de wortel. Je zult de wortels moeten vinden door de berekeningsvolgorde te volgen waar we het net boven deze lijst over hadden (met de afbeeldingen).
- We drukken de wortel uit in de vorm (x – a): als we alle wortels van de polynoom hebben, moeten we ze in de volgende vorm uitdrukken (x – a). Rekening houdend met het feit dat a de waarden zijn die we hebben verkregen, als we bijvoorbeeld als resultaat x = 2, x = -2 en x = 4 extraheren, dan verkrijgen we (x – 2), (x + 2) en ( x-4).
- We verzamelen alle factoren in één enkele uitdrukking: als we uiteindelijk alle wortels al in het juiste formaat hebben uitgedrukt, hoeven we ze alleen maar in één enkele algebraïsche uitdrukking te verzamelen. Als we verdergaan met het vorige voorbeeld, zouden we zoiets als dit hebben: (x – 2) · (x + 2) · (x – 4).
Ontbind een polynoom in factoren met behulp van de wortels van een polynoom
We hebben het basisconcept van een polynoom voor de helft uitgelegd in de sectie van Ruffini. Maar de exacte definitie zou zijn: de wortel van een polynoom P(x) is een numerieke waarde a, zodat P(a) = 0 . Het is dus een getal dat de betreffende functie of polynoom kan opheffen. Samenvattend zouden we kunnen zeggen dat het wordt gebruikt om een polynoom te ontbinden in een product van factoren.
Als we bijvoorbeeld de volgende uitdrukking x² − x − 2 krijgen en we deze ontbinden in factoren met behulp van de regel van Ruffini of door simpelweg de kwadratische vergelijking x² − x − 2 = 0 op te lossen, krijgen we twee x-waarden = -1 en x = 2, dus als we ze veranderen in het formaat (x – a) en ze samenvoegen, komen we uit op de volgende uitdrukking: (x + 1) (x − 2), dat wil zeggen de gefactoriseerde polynoom . En we kunnen dit toepassen op polynomen met een graad groter dan twee, ook al bestaat de uitdrukking uit meer dan één term.
Een polynoom in factoren ontbinden door extractie van gemeenschappelijke factoren
Als we polynomen willen ontbinden zonder een onafhankelijke term of uitdrukkingen die in alle termen een gemeenschappelijke factor hebben, dan kunnen we de polynoom vereenvoudigen met behulp van deze techniek. Het gaat in feite om het toepassen van de distributieve eigenschap op de hele uitdrukking, het verwijderen van de herhalende gemeenschappelijke factor en het toevoegen ervan door de hele polynoom te vermenigvuldigen. Hieronder vindt u een voorbeeld van het eerste geval waar we het over hadden (polynoom zonder onafhankelijke term):
2x³ + 10x² – 6x = 2x (x² + 5x – 3)
Dubbele extractie van de gemeenschappelijke factor
Gemeenschappelijke factorextractie kan zelfs worden gedaan door complexere factoren te extraheren, die meerdere variabelen omvatten. En je kunt zelfs polynomen extraheren die zijn afgeleid van de hoofduitdrukking zelf. Het is belangrijk om geen grenzen te stellen als u dit soort bewerkingen wilt uitvoeren, omdat het doel van factorextractie is om een algebraïsche uitdrukking zoveel mogelijk te vereenvoudigen .
Factoring van polynomen met behulp van opmerkelijke identiteiten
Opmerkelijke producten kunnen ons helpen polynoomuitdrukkingen te ontbinden, omdat het een soort vereenvoudigde algebraïsche uitdrukkingen zijn. Ze helpen ons daarom direct van een lange polynoom naar een kleine formule te gaan die uit een paar termen bestaat. Het wordt daarom sterk aanbevolen om de formules van opmerkelijke identiteiten te leren, zodat u snel kunt identificeren wanneer u ze kunt gebruiken. En daardoor besparen we tijd bij het gebruik van Ruffini of een van de andere methoden. Vervolgens bespreken we de drie regels die u moet leren:
- Verschil in vierkanten: a² – b² = (a + b) · (a – b)
- Kwadraat van de som: a² + 2ab + b² = (a + b)²
- Aftrekkingsvierkant: a² – 2ab + b² = (a – b)²
Polynomen in factoren ontbinden door te groeperen
In sommige gevallen kunnen we een polynoom van structuur x² – ax – bx + ab vinden, die vereenvoudigd kan worden door een gemeenschappelijke factor te verwijderen: x (x – a) – b (x – a). En als we opnieuw de gemeenschappelijke factor nemen, kan deze verder vereenvoudigd worden: (x – a) · (x – b). Daarom zouden de wortels van dit polynoom x = a en x = b zijn. Zoals je kunt zien, heeft dit type algebraïsche expressie een structuur die heel gemakkelijk te ontbinden en te gebruiken is.
Polynomiale factorisatie-oefeningen
Ten slotte willen we u een reeks oefeningen aanbieden waarmee u kunt oefenen met het ontbinden van polynomen. Op deze manier kun je de theorie die we vandaag hebben uitgelegd beter internaliseren. U hoeft alleen maar de oefeningen in uw notitieboekje op te lossen en vervolgens de resultaten te vergelijken met de resultaten die wij u hieronder aanbieden.
- x 4 -1 = (x 2 + 1) (x + 1) (x – 1)
- x 5 + x 4 – x – 1 = (x – 1) (x + 1) 2 (x 2 + 1)
- 9×2 + 30x + 25 = (3x + 5) 2
- x 4 – 3x 3 – 3x 2 + 11x – 6 = (x + 2) (x – 3) (x – 1) 2