Exponentiële functies: kenmerken, grafische weergave, oefeningen,...

Op deze pagina ontdek je wat exponentiële functies zijn en ook hoe je een exponentiële functie in een grafiek kunt weergeven. Bovendien ziet u alle kenmerken ervan en verschillende voorbeelden om het volledig te begrijpen. Ten slotte kun je oefenen met oefeningen en stap voor stap opgeloste problemen op exponentiële functies.

Wat is een exponentiële functie?

De definitie van een exponentiële functie is als volgt:

In de wiskunde zijn exponentiële functies functies die de onafhankelijke variabele x hebben in de exponent van een macht. Met andere woorden, ze zijn als volgt:

$f(x)=a^x$

Goud

$a$

is een positief reëel getal en verschilt van 1.

Voorbeelden van exponentiële functies

De volgende functies zijn voorbeelden van exponentiële functies:

$f(x)=3^{x}$

$f(x)=4^{-x}$

$\displaystyle f(x)=\left( \frac{1}{2} \right)^x$

$f(x)=5^x$

Kenmerken van exponentiële functies

Exponentiële functies hebben de volgende eigenschappen:

Het domein van een exponentiële functie bestaat uit reële getallen, of met andere woorden: er bestaat een exponentiële functie voor elke waarde van x .

$\text{Dom } f=\mathbff{R}$

De functie neemt echter alleen positieve waarden aan, dus het bereik van een exponentiële functie bestaat uit positieve reële getallen.

$\text{Im } f= (0,+\infty)$

Elke exponentiële functie is zowel een continue als een injectieve functie.

Als de functie niet wordt vertaald, gaat elke exponentiële functie door het punt (0,1). Omdat de functie die op nul wordt geëvalueerd, altijd één oplevert.

$f(0)=a^0=1$

Op dezelfde manier is de waarde van een exponentiële functie bij x=1 gelijk aan de basis.

$f(1)=a^1=a$

Als de machtsbasis
$(a)$

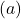
groter is dan 1, neemt de exponentiële functie toe. Aan de andere kant, als de coëfficiënt

$a$

zich in het interval tussen 0 en 1 bevindt, neemt de exponentiële functie af.

Over het algemeen is de x-as een horizontale asymptoot van een exponentiële functie.

Het omgekeerde van de exponentiële functie is de logaritmische functie. Daarom zijn de grafieken van een exponentiële functie en een logaritmische functie symmetrisch rond de lijn y=x als beide dezelfde basis hebben.

Hoe u een exponentiële functie kunt tekenen

Exponentiële functies zijn heel eenvoudig weer te geven. Laten we dus eens kijken hoe we een exponentiële functie in een grafiek kunnen weergeven aan de hand van een voorbeeld.

Teken de volgende exponentiële functie in een grafiek:

$f(x)=2^x$

Bij exponentiële functies is het niet nodig om het domein te berekenen, omdat het altijd allemaal reële getallen zullen zijn:

$\text{Dom } f = \mathbb{R}$

Het is daarom voldoende om de waardentabel op te stellen. Omdat dit soort functies van het ene punt naar het andere veel veranderen, berekenen we 5 punten. Maar hoe meer punten we berekenen, hoe nauwkeuriger de weergave van de functie zal zijn.

$x= 0 \ \longrightarrow \ f(0)=2^0= 1$

$x= 1 \ \longrightarrow \ f(1)=2^1= 2$

$x= 2 \ \longrightarrow \ f(2)=2^2= 4$

$x= -1 \ \longrightarrow \ f(-1)=2^{-1}= 0,5$

$x= -2 \ \longrightarrow \ f(-2)=2^{-2}= 0,25$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 1 \\ 1 & 2 \\ 2 & 4 \\ -1 & 0,5 \\ -2 & 0,25 \end{array}$

We raden u aan een rekenmachine te gebruiken om de punten in de waardentabel te vinden, omdat deze ingewikkeld zijn om met de hand te berekenen.

Nu geven we de punten weer in een grafiek :

En tot slot voegen we de punten samen en breiden we de functie uit:

hoe u een exponentiële functie kunt weergeven of tekenen

Merk op dat de functie aan de rechterkant blijft groeien tot in het oneindige.

De functie aan de linkerkant neemt daarentegen af, maar bereikt nooit 0. Hoewel hij er heel dichtbij komt, raakt hij hem nooit aan. Dit betekent dat de lijn y=0 (de x-as) een horizontale asymptoot is.

Opgeloste oefeningen over exponentiële functies

Oefening 1

Teken de volgende exponentiële functie:

$f(x)= 2^x+1$

Zie de oplossing

Het is een exponentiële functie, dus om deze weer te geven moet je een tabel met waarden maken die waarden geeft aan de variabele x:

$x= 0 \ \longrightarrow \ f(0)= 2^0+1=2$

$x= 1 \ \longrightarrow \ f(1)= 2^1+1=3$

$x= 2 \ \longrightarrow \ f(2)= 2^2+1=5$

$x= -1 \ \longrightarrow \ f(-1)= 2^{-1}+1=1,5$

$x= -2 \ \longrightarrow \ f(-2)= 2^{-2}+1=1,25$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 2 \\ 1 & 3 \\ 2 & 5 \\ -1 & 1,5 \\ -2 & 1,25 \end{array}$

Zodra we de waardentabel hebben, plotten we de verkregen punten in de grafiek en plotten we de functie:

oefening stap voor stap opgelost van exponentiële functies

Merk op dat de functie aan de rechterkant blijft groeien tot in het oneindige. Aan de andere kant neemt de functie aan de linkerkant af maar overschrijdt nooit 1. De functie heeft inderdaad een horizontale asymptoot aan de rechterkant y=1.

In dit geval bevindt de horizontale asymptoot zich op y=1 in plaats van op de OX-as, omdat er een verticale vertaling van één eenheid naar boven naar de functie is gemaakt.

Oefening 2

Teken de volgende exponentiële functie in een grafiek:

$\displaystyle f(x)= \left(\frac{1}{3}\right)^x$

Zie de oplossing

Het is een exponentiële functie, dus om het grafisch weer te geven moet je een tabel met waarden samenstellen die waarden geeft aan de variabele x:

$x= 0 \ \longrightarrow \ f(0)= \left(\cfrac{1}{3}\right)^0 = 1$

$x= 1 \ \longrightarrow \ f(1)= \left(\cfrac{1}{3}\right)^1 = 0,33$

$x= 2 \ \longrightarrow \ f(2)= \left(\cfrac{1}{3}\right)^2 = 0,11$

$x= -1 \ \longrightarrow \ f(-1)= \left(\cfrac{1}{3}\right)^{-1} = 3$

$x= -2 \ \longrightarrow \ f(-2)= \left(\cfrac{1}{3}\right)^{-2} = 9$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 1 \\ 1 & 0,33 \\ 2 & 0,11 \\ -1 & 3 \\ -2 & 9 \end{array}$

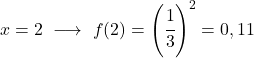
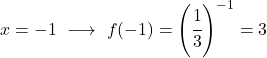
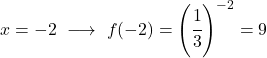
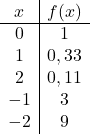
Zodra we de waardentabel hebben, zetten we de berekende punten in de grafiek en tekenen we de functie:

oefeningen met exponentiële functies opgelost

Merk op dat de functie aan de linkerkant blijft groeien tot in het oneindige. Aan de andere kant neemt de functie aan de rechterkant af maar overschrijdt nooit 0. De functie heeft inderdaad een horizontale asymptoot op y=0 (de X-as).

Oefening 3

Teken de volgende exponentiële functie in een grafiek:

$\displaystyle f(x)= \left(\frac{1}{2}\right)^x+3$

Zie de oplossing

Het is een exponentiële functie, dus om deze te tekenen moet je een tabel met waarden maken waarin je de functie op verschillende punten evalueert:

$x= 0 \ \longrightarrow \ f(0)= \left(\cfrac{1}{2}\right)^0+3 = 4$

$x= 1 \ \longrightarrow \ f(1)= \left(\cfrac{1}{2}\right)^1+3 = 3,5$

$x= 2 \ \longrightarrow \ f(2)= \left(\cfrac{1}{2}\right)^2+3 = 3,25$

$x= -1 \ \longrightarrow \ f(-1)= \left(\cfrac{1}{2}\right)^{-1}+3 = 5$

$x= -2 \ \longrightarrow \ f(-2)= \left(\cfrac{1}{2}\right)^{-2}+3 = 7$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 4 \\ 1 & 3,5 \\ 2 & 3,25 \\ -1 & 5 \\ -2 & 7 \end{array}$

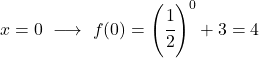
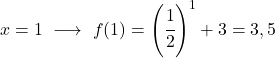
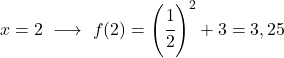
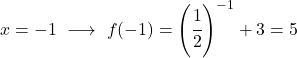
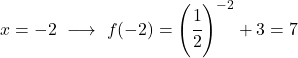
Ten slotte vertegenwoordigen we de verkregen punten in de grafiek en plotten we de functie:

Merk op dat de functie aan de linkerkant onbeperkt groeit naar oneindig. Aan de andere kant, aan de rechterkant, neemt de functie af maar overschrijdt nooit 3. De functie heeft inderdaad een horizontale asymptoot op y=3.

In dit geval bevindt de horizontale asymptoot zich op y=3 in plaats van op de X-as, omdat de functie verticaal drie eenheden naar boven is verplaatst.

Oefening 4

Los het volgende probleem met betrekking tot exponentiële functies op.

Bepaal de waarde van
$k$

zodat de volgende exponentiële functie door het punt (2.8) gaat.

$f(x)=k\cdot 2^x$

Zie de oplossing

De functie moet door het punt (2,8) gaan, dus we kunnen de waarden van x en f(x) van het punt in de functie vervangen om de waarde van de constante k te vinden:

$f(x)=k\cdot 2^x \ \xrightarrow{x \ = \ 2 \ ; \ f(x) \ = \ 8} \ 8 = k \cdot 2^2$

En nu lossen we de resulterende vergelijking op:

$8 = k \cdot 2^2$

$8 = k \cdot 4$

$\cfrac{8}{4} = k$

$\bm{ 2 = k}$

Oefening 5

Los het volgende probleem met betrekking tot exponentiële functies op.

Een populatie termieten plant zich voort volgens de volgende functie:

$f(t)=3^{t+1}$

Goud

$f(t)$

is het aantal termieten en

$t$

de tijd is in maanden verstreken.

Hoeveel termieten zullen er na 1 jaar zijn?

Zie de oplossing

Om te berekenen hoeveel termieten er in een jaar zullen zijn, vervangt u eenvoudigweg de verstreken tijd (1 jaar) in de functie. Maar omdat de functie t de verstreken maanden is en niet de jaren, moeten we t =12 stellen, aangezien er in een jaar 12 maanden zijn:

$f(t)=3^{t+1}$

$f(12)=3^{12+1}$

$f(12)=3^{13}$

We lossen het op met de rekenmachine:

$f(12)= 1594323$

Dus na een jaar zullen er 1.594.323 termieten zijn.

Wat is een exponentiële functie?

Voorbeelden van exponentiële functies

Kenmerken van exponentiële functies

Hoe u een exponentiële functie kunt tekenen

Opgeloste oefeningen over exponentiële functies

Oefening 1

Oefening 2

Oefening 3

Oefening 4

Oefening 5

Laat een reactie achter Reactie annuleren