Expliciete vergelijking van de lijn

Op deze pagina vindt u alles over de expliciete vergelijking van een lijn: wat is het, wat is de formule, rekenvoorbeelden, enz. U vindt ook een gedetailleerde uitleg van wat helling betekent en het snijpunt van de expliciete vergelijking. En bovendien krijg je verschillende voorbeelden te zien en kun je oefenen met oefeningen die stap voor stap worden opgelost.

Wat is de expliciete vergelijking van de lijn?

Bedenk dat de wiskundige definitie van een lijn een reeks opeenvolgende punten is die in dezelfde richting worden weergegeven, zonder krommen of hoeken.

De expliciete lijnvergelijking is dus een manier om elke lijn wiskundig uit te drukken. Om dit te doen, hoeft u alleen maar de helling van de lijn te kennen en het punt waar deze de Y-as snijdt.

Formule voor de expliciete vergelijking van de lijn

De formule voor de expliciete vergelijking van de lijn is:

$y=mx+n$

Goud

$m$

is de helling van de lijn en

$n$

het y-snijpunt, dat wil zeggen de hoogte waarop het de Y-as snijdt.

Laten we eens kijken hoe de expliciete vergelijking van de lijn wordt berekend aan de hand van een voorbeeld:

Schrijf de expliciete vergelijking van de lijn die door het punt gaat
$P(3,1)$

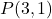
en helling m=2.

De formule voor de expliciete vergelijking van de lijn is:

$y= mx+n$

In dit geval vertelt de verklaring ons dat de helling van de lijn m=2 is, dus de vergelijking van de lijn zal als volgt zijn:

$y= 2x+n$

Het is daarom voldoende om de coëfficiënt n te berekenen. Om dit te doen, moeten we een punt dat bij de lijn hoort in de vergelijking vervangen. En in dit geval vertelt de verklaring ons dat de lijn door het punt gaat

$P(3,1),$

Nog:

$P(3,1)$

$y= 2x+n \ \xrightarrow{x=3 \ ; \ y=1} \ 1=2\cdot 3 +n$

En we lossen de resulterende vergelijking op om de waarde van n te vinden:

$1=2\cdot 3 +n$

$1=6 +n$

$1-6=n$

$-5 = n$

De expliciete vergelijking van de lijn is daarom:

$\bm{y= 2x-5}$

Houd er rekening mee dat er naast de expliciete vergelijking ook andere manieren zijn om een lijn analytisch uit te drukken. Bijvoorbeeld de vectorvergelijking , een soort lijnvergelijking die verschilt van alle andere omdat de richtingsvector en een punt op de lijn worden uitgedrukt met hun eigen coördinaten. In de link zie je wat het is en waarom het zo bijzonder is.

Betekenis van parameters m en n

Zoals we zagen bij de definitie van de expliciete vergelijking van de lijn, de parameter

$m$

is de helling van de lijn en

$n$

het y-snijpunt. Maar wat betekent dat? Laten we dit eens bekijken aan de hand van de grafische weergave van een lijn:

Wat is de expliciete vergelijking van de lijn y=mx+b

De term onafhankelijk

$\bm{n}$

is het snijpunt van de lijn met de computeras (OY-as). In de grafiek hierboven

$n$

is gelijk aan 1 omdat de lijn de y-as snijdt op y=1.

Aan de andere kant, de term

$\bm{m}$

geeft de helling van de lijn aan , dat wil zeggen de helling ervan. Zoals je in de grafiek ziet,

$m$

is gelijk aan 2 omdat de lijn 2 verticale eenheden stijgt voor 1 horizontale eenheid.

Het is duidelijk dat als de helling positief is, de functie toeneemt (omhoog), maar als de helling negatief is, neemt de functie af (omlaag).

Bereken de helling van een lijn

Verder zijn er 3 verschillende manieren om de helling van een lijn numeriek te bepalen:

Gegeven twee verschillende punten op de lijn
$P_1(x_1,y_1)$

En

$P_2(x_2,y_2),$

De helling van de lijn is gelijk aan:

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}$

Ja
$\vv{\text{v}}= (\text{v}_1,\text{v}_2)$

is de richtingsvector van de lijn, de helling is:

$m = \cfrac{\text{v}_2}{\text{v}_1}$

Ja
$\alpha$

is de hoek gevormd door de lijn met de abscis-as (X-as), de helling van de lijn is gelijk aan de raaklijn van genoemde hoek:

$m = \text{tg}(\alpha )$

formule voor de expliciete vergelijking van de lijn

Relatieve positie van lijnen

Ten slotte wordt de helling van een lijn ook gebruikt om de relatie tussen verschillende lijnen te kennen. Omdat twee parallelle lijnen dezelfde helling hebben en, aan de andere kant, als de helling van één lijn het negatieve omgekeerde is van de helling van een andere lijn, betekent dit dat deze twee lijnen loodrecht staan.

Bereken de expliciete vergelijking van de lijn die door twee punten gaat

Een heel typisch probleem is het vinden van de expliciete vergelijking van een lijn gegeven twee punten waar deze doorheen gaat. Laten we eens kijken hoe het wordt opgelost aan de hand van een voorbeeld:

Bepaal de expliciete vergelijking van de lijn die door de volgende twee punten gaat:

$P_1(4,-1) \qquad P_2(2,5)$

Om de expliciete vergelijking van de lijn te vinden, moet je weten wat de parameters m en n waard zijn. We berekenen dus eerst de helling van de lijn met behulp van de dubbele puntformule:

$m =\cfrac{\Delta y}{\Delta x}=\cfrac{y_2-y_1}{x_2-x_1} = \cfrac{5-(-1)}{2-4} = \cfrac{6}{-2}= -3$

$y=-3x+n$

En dan kunnen we het y-snijpunt vinden door een punt op de lijn in de vergelijking te vervangen:

$P_1(4,-1)$

$y= -3x+n \ \xrightarrow{x=4 \ ; \ y=-1} \ -1=-3\cdot 4 +n$

$-1 =-12+ n$

$-1 +12= n$

$11= n$

Dus de expliciete vergelijking van de lijn is:

$\bm{y=-3x+11}$

Het vinden van de expliciete vergelijking uit de impliciete vergelijking

Een ander type probleem dat we vaak tegenkomen, is het vinden van de expliciete vergelijking van de lijn op basis van de impliciete vergelijking ervan (ook wel een algemene of cartesiaanse vergelijking genoemd). Om de volgende methode te begrijpen, moet je uiteraard precies weten wat de impliciete vergelijking is en hoe deze is; maar als je het helemaal niet meer weet, kun je het via de link bekijken.

Dus, als je de impliciete (of algemene) vergelijking van een lijn al onder de knie hebt, laten we dan eens kijken hoe deze procedure werkt:

Zoek de expliciete vergelijking van de volgende regel:

$3x-2y+8 =0$

Het enige wat we hoeven te doen om de expliciete vergelijking van de lijn te vinden, is het oplossen van de variabele

$\bm{y}.$

Dus we passeren de voorwaarden zonder

$y$

aan de andere kant van de vergelijking:

$-2y=-3x-8$

Nu wissen we de variabele

$y:$

$\displaystyle y=\frac{-3x-8}{-2}$

En tot slot vereenvoudigen we:

$\displaystyle y=\frac{-3x}{-2} -\cfrac{8}{-2}$

$\displaystyle y=\frac{3x}{2} -(-4)$

$\displaystyle \bm{y=}\frac{\bm{3}}{\bm{2}}\bm{x +4}$

De helling van deze lijn is dus

$\displaystyle \frac{3}{2}$

en het y-snijpunt is 4.

Opgeloste expliciete vergelijkingsproblemen

Oefening 1

Geef de helling en het y-snijpunt van de volgende lijnen:

$\begin{array}{lll} A) \ y= 3x-1 & \qquad & B) \ y=5x+2 \\[2ex] C) \ y=-x+3 & \qquad & D) \ 4x+2y-6=0 \end{array}$

zie oplossing

De expliciete vergelijking van een lijn volgt de volgende formule:

$y=mx+n$

Goud

$m$

is de helling en

$n$

de computer bij de oorsprong. Nog:

$\bm{A)} \ y= 3x-1 \ \begin{cases} m = 3 \\[2ex] n=-1\end{cases}$

$\bm{B)} \ y= 5x+2 \ \begin{cases} m = 5 \\[2ex] n=2 \end{cases}$

$\bm{C)} \ y= -x+3 \ \begin{cases} m = -1 \\[2ex] n=3\end{cases}$

De laatste regel wordt uitgedrukt door de impliciete vergelijking ervan, dus we moeten deze eerst doorgeven aan een expliciete vergelijking (oplossen voor

$y$

) dan kunnen we de parameters identificeren:

$\bm{D)} \ 4x+2y-6=0$

$2y =-4x+6$

$y =\cfrac{-4x+6}{2}$

$y =-2x+3$

$\begin{cases} m = -2 \\[2ex] n=3 \end{cases}$

Oefening 2

Zoek de expliciete vergelijking van de lijn die door het punt gaat

$P(2,-3)$

en heeft de helling

$m=-2.$

zie oplossing

De formule voor de expliciete vergelijking van de lijn is:

$y= mx+n$

In dit geval moet de helling van de lijn -2 zijn, dus de vergelijking van de lijn heeft de volgende vorm:

$y= -2x+n$

Het is daarom voldoende om de coëfficiënt n te berekenen. Om dit te doen, moet je een punt dat bij de lijn hoort in de vergelijking vervangen en de resulterende vergelijking oplossen:

$P(2,-3)$

$y= -2x+n \ \xrightarrow{x=2 \ ; \ y=-3} \ -3=-2\cdot 2 +n$

$-3=-4 +n$

$-3+4= n$

$1= n$

Kortom, de expliciete vergelijking van de lijn is:

$\bm{y= -2x+1}$

Oefening 3

Zoek de expliciete vergelijking van de lijn die door de volgende twee punten gaat:

$P_1(6,-1) \qquad P_2(3,2)$

zie oplossing

Om de expliciete vergelijking van de lijn te vinden, moet je weten wat de parameters m en n waard zijn. We berekenen daarom eerst de helling van de lijn op basis van de coördinaten van de twee punten:

$m = \cfrac{\Delta y}{\Delta x}=\cfrac{y_2-y_1}{x_2-x_1} = \cfrac{2-(-1)}{3-6} = \cfrac{3}{-3}= -1$

$y=-x+n$

En dan bepalen we het snijpunt door een punt op de lijn in de vergelijking te vervangen:

$P_1(6,-1)$

$y= -x+n \ \xrightarrow{x=6 \ ; \ y=-1} \ -1=-6 +n$

$-1 +6= n$

$5= n$

Dus de expliciete vergelijking van de lijn is:

$\bm{y=-x+5}$

Oefening 4

Bereken de expliciete vergelijking van de lijn die een hoek van 45º vormt met de X-as en door de oorsprong van de coördinaten gaat.

zie oplossing

Als de lijn een hoek van 45 graden maakt met de OX-as, is de helling:

$m = \text{tg}(45º) = 1$

$y=x+n$

En zodra we de helling van de lijn kennen, kunnen we het y-snijpunt berekenen door een punt op de lijn in de vergelijking te vervangen. Bovendien vertelt de verklaring ons dat de lijn door de coördinaatoorsprong gaat, wat betekent dat deze door het punt (0,0) gaat. Nog:

$P(0,0)$