Op deze pagina vindt u de betekenis van de excentriciteit van de ellips en hoe deze wordt berekend (formule). Daarnaast ziet u voorbeelden van ellips-excentriciteitsberekeningen.
Wat is de excentriciteit van de ellips?
Ellips-excentriciteit is een parameter die meet hoe rond of afgeplat een ellips is, dat wil zeggen dat de excentriciteit van een ellips aangeeft hoeveel de ellips op een cirkel lijkt.
Laten we ons aan de andere kant ook herinneren waaruit een ellips bestaat: de ellips is de meetkundige plaats van alle punten van een vlak waarvan de som van de afstanden tot twee andere vaste punten (de zogenaamde brandpunten F en F’) constant is.
Ellips-excentriciteitsformule
Als we eenmaal de definitie van de excentriciteit van de ellips hebben gezien, gaan we kijken hoe deze wordt berekend op basis van de formule:
De formule voor de excentriciteit van de ellips is als volgt:
![]()
Goud:
-

is de excentriciteit van de ellips
-

is de afstand van een brandpunt (punten F en F’) van de ellips tot het midden ervan
-

is de lengte van de semi-hoofdas (of hoofdas) van de ellips.
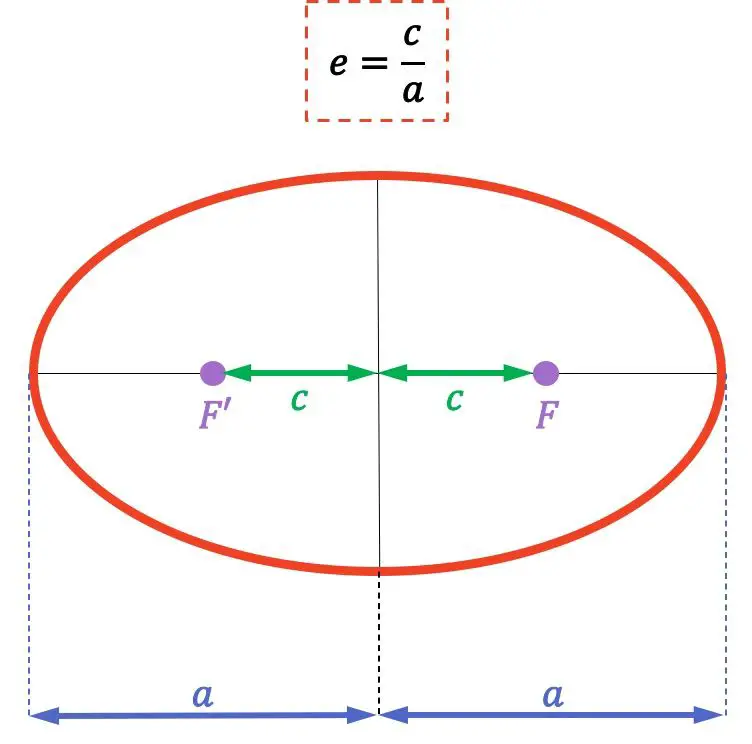
Bedenk dat de brandpunten van een ellips de vaste punten zijn waarvan de som van de afstanden tot elk punt op de ellips constant is. Bovendien wordt de afstand tussen de twee brandpunten de brandpuntsafstand genoemd.
De excentriciteitswaarde varieert van nul, wat betekent dat het een perfecte cirkel is, tot één, wat betekent dat het een horizontale lijn is. Het is duidelijk dat 0 en 1 niet zijn opgenomen omdat de resulterende geometrische objecten niet langer ellipsen zijn.

![]()
d(P,F)
![]()
d(P,F’)
![]()
heeft
![]()
heeft

![]()
heeft
![]()
versus,
![]()
e= \cfrac{c}{a} = \cfrac{4}{5} = \bm{0,8} $