Enkelvoudige rente is de meest gebruikelijke manier om rente te berekenen en wordt voor verschillende doeleinden gebruikt, van het kopen van een huis tot het afsluiten van een persoonlijke lening. Als u ooit enkelvoudige rente moet berekenen, laat deze gids u stap voor stap zien hoe u dit moet doen. We bieden u ook een online calculator om uw taak gemakkelijker te maken.
Eenvoudige rentecalculator
Deze online rekenmachine voor enkelvoudige rente is een hulpmiddel waarmee u alle variabelen kunt berekenen die betrokken zijn bij het berekenen van enkelvoudige rente. Om het te gebruiken, selecteert u eenvoudigweg wat u wilt berekenen en voert u de gegevens in voor de variabelen waar het om vraagt. Vervolgens moet u op de knop Berekenen klikken en dat is alles.
Wat is enkelvoudige rente?
Enkelvoudige rente is de rente die in rekening wordt gebracht als u voor een bepaalde periode een bedrag belegt of leent . Het wordt berekend door het initiële bedrag te vermenigvuldigen met het rentepercentage en de tijd. Samenvattend wordt deze rente gebruikt bij constante en normaal gesproken kortetermijn financiële acties.
Omdat het rentepercentage en de looptijd constant worden gehouden, is de rente die maandelijks of jaarlijks moet worden betaald altijd hetzelfde , aangezien de rente niet stijgt. Dit is het belangrijkste verschil tussen enkelvoudige rente en samengestelde rente .
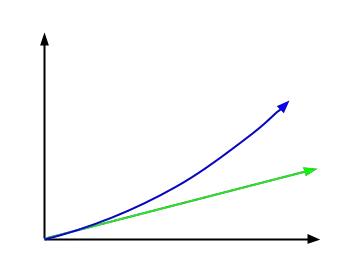
In de volgende afbeelding ziet u de functie die enkelvoudige rente vertegenwoordigt in groen en de samengestelde rentefunctie, weergegeven in blauw. Zoals we in de afbeelding kunnen zien, heeft het een veel exponentiële vorm.
Formule om enkelvoudige rente te berekenen
De formule voor het berekenen van enkelvoudige rente is: I = C xixt , waarbij de volgende variabelen een rol spelen:
- Startkapitaal (C): som van het geïnvesteerde of geleende geld, waarover enkelvoudige rente wordt berekend.
- Rentepercentage (i): deze indicator vertelt ons als percentage het rentebedrag in verhouding tot de tijd. Het is belangrijk om dit in de formule met één te schrijven (deel de procentuele waarde door honderd).
- Tijd (t): De lengte van de investeringsperiode, doorgaans uitgedrukt in jaren. Hoewel we je hieronder leren hoe je het naar andere tijdseenheden kunt converteren, zoals: maanden en dagen.
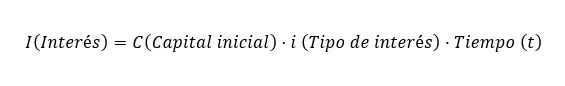
Om te zien hoe deze formule wordt gebruikt, kunnen we het volgende voorbeeld bekijken: we hebben € 1000 belegd tegen een jaarlijkse rentevoet van 4%. Hoeveel rente zullen we na drie jaar hebben gegenereerd? Om de gegenereerde rente te vinden, moeten we de formule toepassen: I = C x (i ÷ 100) xt = 1000 x (4 ÷ 100) x 3 = €120.
Vervolgens kunnen we uit de hoofdformule de verschillende variabelen isoleren en zo de formules verkrijgen waarmee we het startkapitaal, de rentevoet, de tijd en het eindkapitaal kunnen berekenen. En dit is wat we zullen zien in de volgende secties, waar we je zullen leren hoe je deze variabelen kunt berekenen op basis van de formule die je al hebt gezien, en nog een heel eenvoudige.
Hoe wordt het eindkapitaal berekend?
Om het uiteindelijke kapitaal te berekenen, past u eenvoudigweg logica toe. Omdat het eindbedrag gelijk is aan het beginbedrag, is de formule, nadat we de rente hebben toegepast, als volgt: Eindkapitaal (Cf) = Beginkapitaal (C) + Rente (I). Deze uitdrukking is de op een na belangrijkste enkelvoudige renteformule, waarvan de belangrijkste de vorige is.
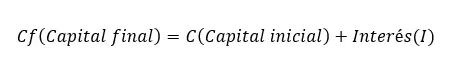
Nu u de formule kent, kunt u dit praktijkvoorbeeld proberen op te lossen: Wat is het uiteindelijke kapitaal dat u krijgt als u gedurende 4 jaar € 50.000 belegt, met een rente van € 20.000? We passen eenvoudigweg de uitdrukking van voorheen toe: Eindkapitaal (Cf) = Beginkapitaal (C) + Rente (I) = 50.000 + 20.000 = € 70.000.
Hoe wordt het startkapitaal berekend?
Als we het startkapitaal willen berekenen, kunnen we twee formules gebruiken, afhankelijk van de gegevens die ze ons geven. Ten eerste kunnen we de uitdrukking uit de vorige sectie toepassen als we het eindkapitaal hebben en het bedrag dat door de rente wordt gegenereerd: Beginkapitaal (C) = Eindkapitaal (Cf) – Rente (I).
Ten tweede kunnen we de waarde van het startkapitaal isoleren in de enkelvoudige renteformule (waar we het in het begin over hadden). We zouden dus een startkapitaal (C) = rente (I) ÷ (tijd (t) x rentepercentage (i)) overhouden.

Laten we een voorbeeld bekijken van het tweede, complexere geval: Hoeveel moet ik investeren om rente te krijgen over € 30.000, met een rente van 8% gedurende 2 jaar? We passen de formule Beginkapitaal = I ÷ (tx (i ÷ 100)) toe, wat ons een initieel bedrag van 30.000 ÷ (2 x (8 ÷ 100)) = € 187.500 oplevert.
Hoe wordt de rente berekend?
Om het rentepercentage te berekenen, moeten we ook de enkelvoudige renteformule gebruiken, maar isoleren we de i. Daarom houden we het volgende over: rentepercentage (i) = rente (I) ÷ (aanvangskapitaal (C) x tijd (t)). Zoals u kunt zien, zijn alle formules hetzelfde, maar isoleren ze een andere variabele.
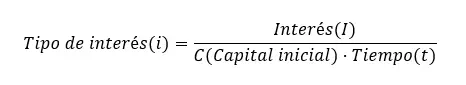
Hier is een praktisch voorbeeld van het berekenen van de rente: tegen welk rentetarief moeten we € 180.000,- gedurende vijf jaar investeren, als we dit willen omzetten in € 200.000,-? In dit voorbeeld moet u eerst de rente vinden: I = Cf – C = 200.000 – 180.000 = € 20.000. En dan lossen we op: Rente = 20.000 ÷ (180.000 x 5) = 0,022 x 100 = 2,2%.
Hoe wordt de tijd berekend?
Ten slotte kunnen we de tijd berekenen, die ook kan worden verkregen uit de initiële formule: Tijd (t) = Rente (I) ÷ (Beginbedrag (C) x Rentepercentage (i)). Het is belangrijk om te onthouden dat de formule vereist dat de tijdseenheden jaren zijn. Als u het echter in andere eenheden wilt uitdrukken, kunt u de volgende varianten van de formule gebruiken:
- I = C · (i / 100) · t als t jaren zijn (algemene formule)
- I = C · (i / 1200) · t als t maanden zijn (Resultaat in maanden)
- I = C · (i / 36000) · t als t dagen zijn (resultaat in dagen)
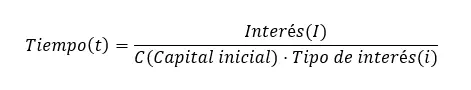
Kijk eens naar het volgende voorbeeld: Hoeveel tijd moet er verstrijken als we willen dat een investering van € 40.000 een rente genereert van € 5.000, met een rentepercentage van 5%? De berekening blijft: Tijd = 5.000 ÷ (40.000 x 5 ÷ 100) = 2,5 jaar. Als we het echter in maanden willen berekenen, kunnen we het volgende doen: Tijd = 5.000 ÷ (40.000 x 5 ÷ 1200) = 30 maanden.
Voorbeeld uit de praktijk van eenvoudige renteberekening
U hebt nu een voorbeeld gezien van het berekenen van elke variabele waaruit de formule voor enkelvoudige rente bestaat. We willen u echter nog een laatste voorbeeld laten zien van de meest voorkomende berekening , namelijk die van belang zelf. Waarmee je de eerste formule toepast, heb je restjes. Als u de berekening wilt bekijken, vindt u hier een casestudy:
Wij lenen €10.000 om te beleggen en willen berekenen hoeveel geld we na 5 jaar moeten terugbetalen als ze ons een jaarlijkse rente van 3% vragen. De berekening zou zijn:
10.000 x 0,03 = 300
300 x 5 jaar = € 1.500
CF = € 10.000 + € 1.500 = € 11.500
Na vijf jaar zou de rente dus € 1.500 bedragen en het uiteindelijk te betalen kapitaal € 11.500 .
conclusie
Samenvattend moet u bij het berekenen van de enkelvoudige rente rekening houden met het geleende bedrag, het rentepercentage en de looptijd. Van daaruit vermenigvuldigt u eenvoudigweg deze drie getallen om het totale bedrag aan te betalen rente te krijgen. En als u een van de andere variabelen wilt berekenen, hoeft u in plaats van de rente die waarde alleen maar te isoleren in de algemene formule.