Enkelvoudige of gedegenereerde matrix

Op deze pagina zul je zien wat het betekent dat een matrix singulier of gedegenereerd is. Daarnaast laten we u verschillende voorbeelden zien zodat u geen twijfels heeft en tot slot leggen we alle eigenschappen van dit type matrix uit.

Wat is een enkelvoudige of gedegenereerde matrix?

De definitie van een enkelvoudige matrix, ook wel gedegenereerde matrix genoemd, is als volgt:

Een enkelvoudige of gedegenereerde matrix is een vierkante matrix die niet kan worden omgekeerd en daarom is de determinant gelijk aan 0.

Om dus te weten wanneer een matrix singulier is, berekent u eenvoudigweg de determinant ervan: als het resultaat 0 is, is de matrix singulier, aan de andere kant, als de determinant anders is dan 0, is de matrix niet singulier .

Als je meer wilt weten over de inverse matrix, kun je deze pagina raadplegen waar uitgebreid wordt uitgelegd hoe je een matrix kunt omkeren met behulp van de Gauss-methode . Ook vind je er verschillende voorbeelden en oefeningen stap voor stap opgelost om te oefenen.

Aan de andere kant worden enkelvoudige matrices ook wel niet-reguliere matrices genoemd, omdat ze precies het tegenovergestelde van reguliere matrix betekenen.

Voorbeelden van enkelvoudige matrices

Nadat we de uitleg van de enkelvoudige of gedegenereerde matrix hebben gezien, laten we enkele voorbeelden bekijken van enkelvoudige matrices met verschillende dimensies:

Voorbeeld van een 2×2 enkelvoudige matrix

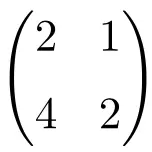
We kunnen eenvoudig verifiëren dat het een singuliere matrix is door de determinant ervan te berekenen:

De determinant van de orde 2-matrix is gelijk aan 0, dus het is een singuliere matrix.

Voorbeeld van 3 x 3 enkelvoudige matrix

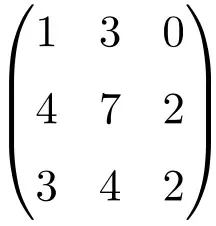
We moeten de determinant van de matrix oplossen om te verifiëren dat het een niet-inverteerbare matrix is:

De determinant van de matrix van orde 3 geeft 0, het is dus een singuliere matrix.

Voorbeeld van een 4 × 4 enkelvoudige matrix

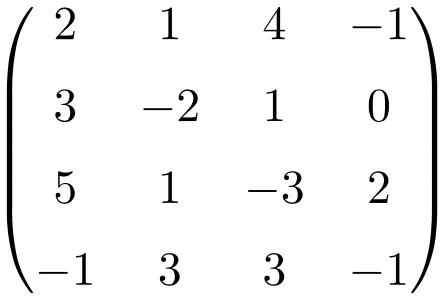
Door de determinant van de matrix te maken, laten we zien dat het een singuliere matrix is:

De determinant van de matrix van orde 4 is nul, dus de inverse matrix bestaat niet.

Waarschuwing: Als u twijfels heeft over de berekeningen van determinanten, kunt u de pagina Hoe berekent u een determinant raadplegen?

Eigenschappen van enkelvoudige matrices

De kenmerken van dit type matrices zijn als volgt:

• Ten minste twee kolommen of twee rijen van een enkelvoudige matrix zijn lineaire combinaties en zijn daarom lineair afhankelijk.

• Elke matrix die een rij of kolom bevat gevuld met nullen, is een enkelvoudige matrix.

• De rangorde van een enkelvoudige of gedegenereerde matrix is kleiner dan de grootte ervan.

• Het matrixproduct van een enkelvoudige matrix vermenigvuldigd met een andere matrix geeft een andere enkelvoudige matrix. Deze voorwaarde kan worden afgeleid uit de eigenschappen van de determinanten:

• Op dezelfde manier is de kracht van een enkelvoudige matrix gelijk aan die van een andere enkelvoudige matrix, ongeacht de kracht waartoe deze wordt verheven.

• De transponering van een enkelvoudige matrix geeft aanleiding tot een andere singuliere matrix, aangezien de determinant van een getransponeerde (of getransponeerde) matrix gelijkwaardig is aan de determinant van de niet-getransponeerde matrix:

• Het vermenigvuldigen van een enkelvoudige matrix met een scalair verandert niets aan de status ervan als gedegenereerde matrix.

• De adjunct van een enkelvoudige matrix is ook enkelvoudig.

• Driehoekige matrices en diagonale matrices zijn gedegenereerde matrices als ten minste één element van hun hoofddiagonaal nul is.

• Het is duidelijk dat de nulmatrix een enkelvoudige matrix is.

• Op dezelfde manier is een nilpotente matrix ook een enkelvoudige matrix.

• Een systeem van lineaire vergelijkingen geassocieerd met een enkelvoudige matrix heeft geen oplossing of heeft oneindig veel oplossingen.

• Ten slotte is een vierkante matrix enkelvoudig als deze ten minste één eigenwaarde (of eigenwaarde) gelijk aan 0 heeft.