In dit artikel leggen we uit wat directe evenredigheidsfuncties zijn, wat hun formule is, hoe je ze in een grafiek kunt weergeven en hoe je hun vergelijking vanaf een bepaald punt kunt berekenen.
Wat is een directe evenredigheidsfunctie?
De directe evenredigheidsfunctie is een functie die twee direct proportionele grootheden met elkaar in verband brengt. Om de waarde van de afhankelijke variabele (y) te berekenen, moet daarom de waarde van de afhankelijke variabele (x) worden vermenigvuldigd met de evenredigheidsconstante.
De directe evenredigheidsfunctie wordt ook wel een lineaire functie genoemd.
Houd er rekening mee dat twee hoeveelheden recht evenredig zijn als de ene hoeveelheid in waarde toeneemt terwijl de andere hoeveelheid ook toeneemt, en omgekeerd.
Formule voor de directe evenredigheidsfunctie
De formule die de directe evenredigheidsfunctie definieert is als volgt:
![]()
waarbij y de onafhankelijke variabele is, x de afhankelijke variabele en ym de helling of constante van evenredigheid van de functie.
Zoals u kunt zien, is het met deze formule heel eenvoudig om waarden van de grootte y te berekenen, u hoeft alleen maar de waarde van de grootte x te vermenigvuldigen met de helling van de functie, kenmerkend voor elke directe evenredigheidsfunctie.
Als we bijvoorbeeld de volgende directe evenredigheidsfunctie hebben:
![]()
Als we willen bepalen hoeveel de grootheid y is als x 5 is, hoeven we alleen de helling van functie (3) met 5 te vermenigvuldigen:
![]()
Grafische weergave van een directe evenredigheidsfunctie
Vervolgens zullen we zien hoe u directe evenredigheidsfuncties kunt tekenen. Als voorbeeld doen we de volgende oefening:
![]()
Om de directe evenredigheidsfunctie in een grafiek weer te geven, tekent u eenvoudigweg een lijn die door de oorsprong van de coördinaten (punt (0,0)) gaat en de helling van de functie heeft.
In dit geval heeft de functie die we willen representeren een helling van
![]()
Daarom moet de lijn met twee eenheden van y groeien voor elke eenheid van x.
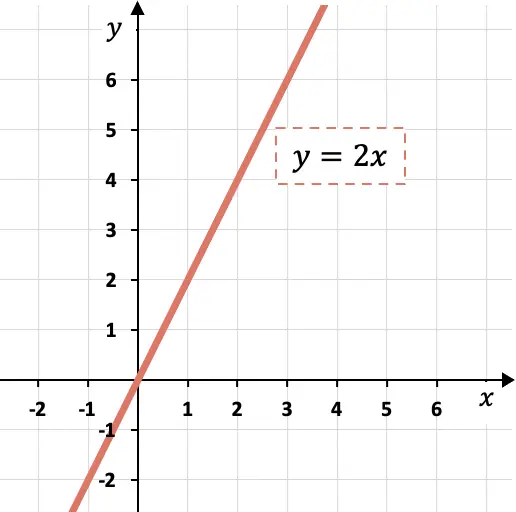
Zoals je in de grafiek kunt zien, betekent dit dat als de helling gelijk is aan 2, de y-grootte twee keer zoveel toeneemt als de x-grootte.
Directe evenredigheidsfuncties hebben een grafiek die sterk lijkt op affiene functies, maar het zijn twee verschillende soorten functies. Je kunt zien wat de verschillen zijn tussen een affiene functie en een lineaire functie in de volgende link:
➤ Zie: verschil tussen lineaire en affiene functie
Hoe de directe evenredigheidsfunctie te vinden
Als we een punt van de directe evenredigheidsfunctie kennen, kunnen we gemakkelijk de vergelijking ervan vinden. Laten we eens kijken hoe dit wordt gedaan door een probleem met de directe evenredigheidsfunctie op te lossen:
- Het aantal kamers dat een schilder schildert is ongeveer recht evenredig met de uren die hij werkt, dat wil zeggen: hoe meer uren hij werkt, hoe meer kamers hij kan schilderen. Als we weten dat hij op een dag van acht uur twee hele kamers heeft geschilderd, wat is dan de directe evenredigheidsfunctie die het aantal geschilderde kamers relateert aan de gewerkte uren?
Eerst moeten we bepalen welke de afhankelijke variabele is en welke de onafhankelijke. Het aantal geschilderde stukken is afhankelijk van de gewerkte uren en niet andersom. Daarom is de onafhankelijke variabele (x) het aantal gewerkte uren en de afhankelijke variabele (y) het aantal geschilderde kamers.
Het probleem vertelt ons dat de schilder in 8 uur twee kamers kan schilderen, dus de grafiek van de functie moet door het punt (8,2) gaan.
![]()
Bovendien geeft de verklaring aan dat de twee grootheden een direct proportioneel verband hebben, wat betekent dat ze wiskundig gerelateerd zijn aan de formule voor de directe evenredigheidsfunctie:
![]()
We kunnen nu de waarde van de helling van de functie berekenen door de coördinaten van het punt (8,2) in de vergelijking te vervangen:
![]()
En ten slotte lossen we de onbekende m van de vergelijking op:
![]()
![]()
![]()
Kort gezegd is de directe evenredigheidsfunctie van het probleem:
![]()
Misschien vind je dit ook leuk: