Op deze pagina zie je wat een diagonaalmatrix is en voorbeelden van diagonaalmatrices. Daarnaast ontdek je hoe je met dit soort matrices kunt werken, hoe je eenvoudig hun determinanten kunt berekenen en hoe je ze kunt omkeren. Er zijn ook eigenschappen en toepassingen van diagonale matrices. En ten slotte zijn er de verklaringen voor een bidiagonale matrix en een tridiagonale matrix.
Wat is een diagonale matrix?
Een diagonaalmatrix is een vierkante matrix waarin alle elementen die niet op de hoofddiagonaal liggen nul (0) zijn. De elementen van de hoofddiagonaal kunnen al dan niet nul zijn.
Zodra we de exacte definitie van een diagonale matrix kennen, zullen we voorbeelden van diagonale matrices zien:
Voorbeelden van diagonale matrices
Voorbeeld van een diagonale matrix met afmeting 2 × 2
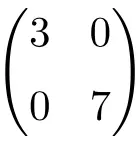
Voorbeeld van een diagonale matrix van orde 3×3

Voorbeeld van een diagonale matrix van maat 4×4
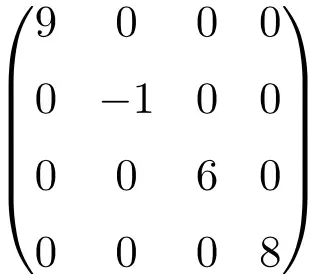
Dit soort matrices worden over het algemeen geschreven en geven de elementen van de diagonaal aan:
![Rendered by QuickLaTeX.com diag(2,5,1) = \left. \begin{pmatrix} 2 & 0 & 0 \\[1.1ex] 0 & 5 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-14216c3a6fd6e7bfd4c9d78ac2a4765c_l3.png)
Bewerkingen met diagonale matrices
Een van de redenen waarom diagonale matrices zo belangrijk zijn voor lineaire algebra is vanwege het gemak waarmee je berekeningen kunt uitvoeren. Dit is de reden waarom ze zo worden gebruikt in de wiskunde.
Diagonale matrices optellen en aftrekken
Het optellen (en aftrekken) van twee diagonale matrices is heel eenvoudig: u hoeft alleen maar de getallen op de diagonalen op te tellen (of af te trekken).
![]()
Bijvoorbeeld:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 0 & -2 & 0 \\[1.1ex] 0 & 0 & 6 \end{pmatrix} +\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & -4 \end{pmatrix} = \begin{pmatrix} 6& 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e659649fca7fe55f33c0f3452e8c46f2_l3.png)
Diagonale matrixvermenigvuldiging
Om een vermenigvuldiging of matrixproduct van twee diagonale matrices op te lossen, vermenigvuldigt u eenvoudigweg de elementen van de diagonalen met elkaar.
![]()
Bijvoorbeeld:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & -4 & 0 \\[1.1ex] 0 & 0 & -3 \end{pmatrix} \cdot\begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 0 & -2 & 0 \\[1.1ex] 0 & 0 & 6 \end{pmatrix} = \begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 0 & 8 & 0 \\[1.1ex] 0 & 0 & -18 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0bcb4a59778cc41eed67dce0bc384682_l3.png)
Kracht van diagonale matrices
Om de macht van een diagonale matrix te berekenen, moeten we elk element van de diagonaal verheffen tot de exponent:
![]()
![]()
Bijvoorbeeld:
![Rendered by QuickLaTeX.com \displaystyle\left. \begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & 4 \end{pmatrix}\right.^3= \begin{pmatrix} 27 & 0 & 0 \\[1.1ex] 0 & 8 & 0 \\[1.1ex] 0 & 0 & 64 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4d27337283f4b6029bff166fb8e3458d_l3.png)
Determinant van een diagonale matrix
De determinant van een diagonale matrix is het product van de elementen op de hoofddiagonaal.
![]()
![]()
Kijk eens naar de volgende opgeloste oefening waarin we de determinant van een diagonaalmatrix vinden door simpelweg de elementen van de hoofddiagonaal te vermenigvuldigen:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 5 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & 3 \end{vmatrix} = 5 \cdot 2 \cdot 3 = 30](https://mathority.org/wp-content/ql-cache/quicklatex.com-f34514c6e1559b8ebb296ee6c51a33d6_l3.png)
Deze stelling is eenvoudig te bewijzen: je hoeft alleen maar de determinant van een diagonale matrix te berekenen met blokken (of cofactoren). Deze demonstratie wordt hieronder gedetailleerd beschreven met behulp van een generieke diagonale matrix:
![Rendered by QuickLaTeX.com \begin{aligned} \begin{vmatrix} a & 0 & 0 \\[1.1ex] 0 & b & 0 \\[1.1ex] 0 & 0 & c \end{vmatrix}& = a \cdot \begin{vmatrix} b & 0 \\[1.1ex] 0 & c \end{vmatrix} - 0 \cdot \begin{vmatrix} 0 & 0 \\[1.1ex] 0 & c \end{vmatrix} + 0 \cdot \begin{vmatrix} 0 & b \\[1.1ex] 0 & 0 \end{vmatrix} \\[2ex] & =a \cdot (b\cdot c) - 0 \cdot 0 + 0 \cdot 0 \\[2ex] & = a \cdot b \cdot c \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7b8718172b4b70d1ccacb01ea7ed5dd4_l3.png)
Keer een diagonale matrix om
Een diagonaalmatrix is inverteerbaar als en slechts als alle elementen van de hoofddiagonaal verschillend zijn van 0 . In dit geval zeggen we dat de diagonale matrix een reguliere matrix is.
Bovendien zal de inverse van een diagonale matrix altijd een andere diagonale matrix zijn met de inverse van de hoofddiagonaal:
![Rendered by QuickLaTeX.com \displaystyle A= \begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & 8 \end{pmatrix} \ \longrightarrow \ A^{-1}=\begin{pmatrix} \frac{1}{3} & 0 & 0 \\[1.1ex] 0 & \frac{1}{2} & 0 \\[1.1ex] 0 & 0 & \frac{1}{8} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a91beaaca82477a0c882b42da4eb7481_l3.png)
Uit het vorige kenmerk kunnen we afleiden dat de determinant van de inverse van een diagonale matrix het product is van de inverse van de hoofddiagonaal:
![Rendered by QuickLaTeX.com \displaystyle B= \begin{pmatrix} 2 & 0 & 0 \\[1.1ex] 0 & 4 & 0 \\[1.1ex] 0 & 0 & -1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0571390802f955fac935aeb9cf4ab92f_l3.png)
![]()
Eigenschappen van diagonale matrices
- Elke diagonale matrix is ook een symmetrische matrix .
- Een diagonale matrix is een matrix die zowel boven- als onderdriehoekig is .
- De identiteitsmatrix is een diagonale matrix:
![Rendered by QuickLaTeX.com \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4e4e9931fb7ae104414006cee93978a7_l3.png)
- Op dezelfde manier is de nulmatrix ook een diagonale matrix, omdat alle elementen die niet op de diagonaal liggen, nullen zijn. Hoewel de cijfers op de diagonaal 0 zijn.
![Rendered by QuickLaTeX.com \begin{pmatrix} 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-edb061dcbc869eba51ece12af43f796f_l3.png)
- De eigenwaarden (of eigenwaarden) van een diagonale matrix zijn de elementen van de hoofddiagonaal.
![Rendered by QuickLaTeX.com \begin{pmatrix} 7 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & 4 \end{pmatrix} \longrightarrow \ \lambda = 3 \ ; \ \lambda = 4 \ ; \ \lambda = 7](https://mathority.org/wp-content/ql-cache/quicklatex.com-1dea3de2ae28d46194ead012bc001cf0_l3.png)
- Een vierkante matrix is diagonaal als en slechts als deze driehoekig en normaal is.
- De adjunct van een diagonale matrix is een andere diagonale matrix.
Diagonale matrixtoepassingen
Zoals we hebben gezien is het oplossen van berekeningen met diagonale matrices heel eenvoudig, omdat er veel nullen bij de bewerkingen betrokken zijn. Om deze reden zijn ze zeer nuttig op het gebied van de wiskunde en worden ze veel gebruikt.
Om dezelfde reden zijn er zoveel onderzoeken gedaan naar het diagonaliseren van een matrix en is er zelfs een methode ontwikkeld voor het diagonaliseren van matrices (met behulp van de karakteristieke polynoom).
Daarom zijn diagonaliseerbare matrices ook behoorlijk relevant. Zoals de spectrale ontbindingsstelling, die de voorwaarden vastlegt voor wanneer een matrix diagonaliseerd kan worden en wanneer niet.
bidiagonale matrix
Een bidiagonale matrix is een vierkante matrix waarin alle elementen die niet op de hoofddiagonaal of op de bovenste of onderste diagonaal liggen, 0 zijn.
Bijvoorbeeld:
![Rendered by QuickLaTeX.com \begin{pmatrix} 3 & 2 & 0 \\[1.1ex] 0 & -5 & 1 \\[1.1ex] 0 & 0 & 6 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d9acdfc09d0167548ef3f6f5b58d9276_l3.png)
bovenste bidiagonale matrix
![Rendered by QuickLaTeX.com \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 6 & 2 & 0 \\[1.1ex] 0 & 7 & 4 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b2b53f238add73431696006f4b05a2d8_l3.png)
lagere bidiagonale matrix
Wanneer de hoofddiagonaal en de eerste superdiagonaal bezet zijn, spreken we van een bovenste bidiagonale matrix. Aan de andere kant, wanneer de hoofddiagonaal en de eerste subdiagonaal bezet zijn, spreken we van een lagere bi-diagonale matrix.
tridiagonale matrix
Een tridiagonale matrix is een vierkante matrix waarvan de enige niet-nul elementen die van de hoofddiagonaal en de aangrenzende diagonalen boven en onder zijn.
Bijvoorbeeld:
![Rendered by QuickLaTeX.com \begin{pmatrix} 2 & 3 & 0 & 0 \\[1.1ex] -4 & 5 & 9 & 0 \\[1.1ex] 0 & 1 & 6 & -2 \\[1.1ex] 0 & 0 & 8 & 7 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9a8fbe0404c447268a89ff954e3b23d5_l3.png)
Alle diagonale, bidiagonale en tridiagonale matrices zijn dus voorbeelden van bandmatrices . Omdat een bandmatrix die matrix is die al zijn niet-nulelementen rond de hoofddiagonaal heeft.