Hoe de determinant van een 2×2-matrix te berekenen

Op deze pagina leer je wat de determinant van een 2×2 matrix is. Daarnaast vindt u stapsgewijze opgeloste voorbeelden en oefeningen over het oplossen van determinanten van orde 2, zodat u dit perfect kunt oefenen en begrijpen.

Wat is een 2×2-determinant?

Een determinant van orde 2 is een matrix met dimensie 2 × 2 , weergegeven door een verticale balk aan elke kant van de matrix. Als we bijvoorbeeld de volgende matrix hebben:

\displaystyle A = \begin{pmatrix} 3 & 1 \\[1.1ex] 5 & 2 \end{pmatrix}

De determinant van matrix A wordt als volgt weergegeven:

\displaystyle \lvert A \rvert = \begin{vmatrix} 3 & 1 \\[1.1ex] 5 & 2 \end{vmatrix}

Zoals je hebt gezien, is het schrijven van de determinant van een vierkante matrix van 2×2 eenvoudig. Laten we nu eens kijken hoe het wordt berekend:

Hoe los je een determinant van orde 2 op?

Om de determinant van een 2×2-matrix te berekenen, moeten we de elementen van de hoofddiagonaal vermenigvuldigen en het product van de secundaire diagonaal aftrekken.

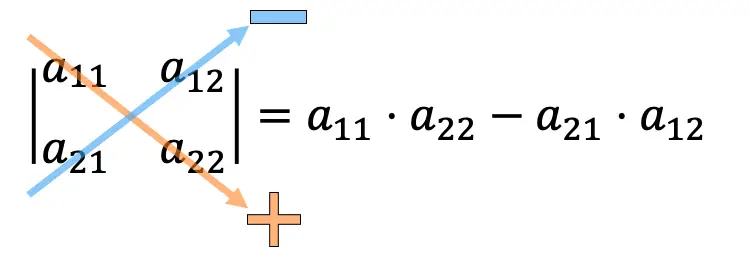
voorbeeld van het berekenen van de determinant van een 2x2-matrix

Voorbeelden van het berekenen van 2×2 determinanten:

\displaystyle\begin{vmatrix} 3 & 4 \\[1.1ex] 2 & 1 \end{vmatrix} = 3 \cdot 1 - 2 \cdot 4 = 3 - 8 = \bm{-5}

\displaystyle\begin{vmatrix} 2 & -3 \\[1.1ex] 1 & 5 \end{vmatrix} = 2 \cdot 5 - 1 \cdot (-3) =10-(-3) = 10+3= \bm{13}

Opgeloste problemen van determinanten van 2 × 2 matrices

Oefening 1

Bereken de volgende 2×2 determinant:

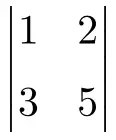
oefening stap voor stap opgelost van de determinant 2x2

Om een 2×2 determinant te maken, moet je de elementen van de hoofddiagonaal vermenigvuldigen en het product van de secundaire diagonaal aftrekken:

\displaystyle \begin{vmatrix} 1 & 2 \\[1.1ex] 3 & 5 \end{vmatrix} = 1 \cdot 5 - 3 \cdot 2 = 5 - 6 = \bm{-1}

Oefening 2

Los de volgende determinant van afmeting 2×2 op:

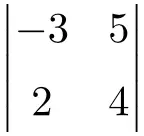
oefeningen stap voor stap opgelost van 2x2 determinanten

Om de oplossing voor een determinant van orde 2 te vinden, moet je de elementen van de hoofddiagonaal vermenigvuldigen en het product van de secundaire diagonaal aftrekken:

\displaystyle \begin{vmatrix} -3 & 5 \\[1.1ex] 2 & 4 \end{vmatrix} = -3 \cdot 4 - 2 \cdot 5 = -12 - 10 = \bm{-22}

Oefening 3

Vind de oplossing voor de volgende determinant van orde 2:

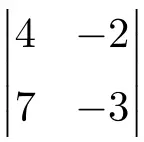
oefening stap voor stap opgelost van een determinant van een 2x2 matrix

Om de oplossing voor een determinant van dimensie 2 te vinden, moet je de elementen van de hoofddiagonaal vermenigvuldigen en het product van de secundaire diagonaal aftrekken:

\displaystyle \begin{vmatrix} 4 & -2 \\[1.1ex] 7 & -3\end{vmatrix} = 4 \cdot (-3) - 7 \cdot (-2) = -12 - (-14) =-12+14= \bm{2}

Oefening 4

Bereken de volgende 2×2 determinant:

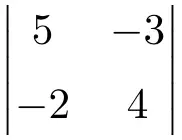
hoe je de determinant van een 2x2 matrix oplost, oefening stap voor stap opgelost

Om de determinanten van 2×2 matrices te berekenen, moeten we de elementen van de hoofddiagonaal vermenigvuldigen en het product van de secundaire diagonaal aftrekken:

\displaystyle \begin{vmatrix} 5 & -3 \\[1.1ex] -2 & 4\end{vmatrix} = 5 \cdot 4 - (-2) \cdot (-3) = 20 - (+6) = \bm{14}

Oefening 5

Bepaal het resultaat van de volgende 2×2 determinant:

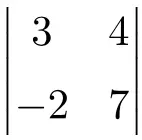
Opgeloste oefening over het stapsgewijs oplossen van de determinant van een orde 2 matrix

Om de oplossing voor een 2×2 determinant te vinden, moeten we de elementen van de hoofddiagonaal vermenigvuldigen en het product van de secundaire diagonaal aftrekken:

\displaystyle \begin{vmatrix} 3 & 4 \\[1.1ex] -2 & 7\end{vmatrix} = 3 \cdot 7 - (-2) \cdot 4 = 21 - (-8)=21+8 = \bm{29}

Helder! Je weet nu hoe je determinanten van dimensie 2×2 kunt maken! Nu kun je vast al begrijpen hoe de 3×3-determinant wordt berekend en ook hoe de determinant van een 4×4-matrix wordt opgelost.

Laat een reactie achter

Je e-mailadres wordt niet gepubliceerd. Vereiste velden zijn gemarkeerd met *

Scroll naar boven