Op deze pagina leggen we uit wat de delen van een monomial zijn (coëfficiënt, letterlijk deel, graad, etc.) en hoe je ze gemakkelijk kunt identificeren. Bovendien kun je voorbeelden zien en zelfs oefenen met oefeningen die stap voor stap worden opgelost op de onderdelen van een monomial.
Wat zijn de onderdelen van een monomial?
De onderdelen van een monomial zijn:
- Coëfficiënt : is het getal dat de variabelen (of letters) van de monomial vermenigvuldigt.
- Variabel : zijn elk van de letters die in de monomial voorkomen.
- Letterlijk deel : komt overeen met alle variabelen die de monomial vormen met al zijn exponenten.
- Graad : is de som van alle exponenten van monomiale variabelen.
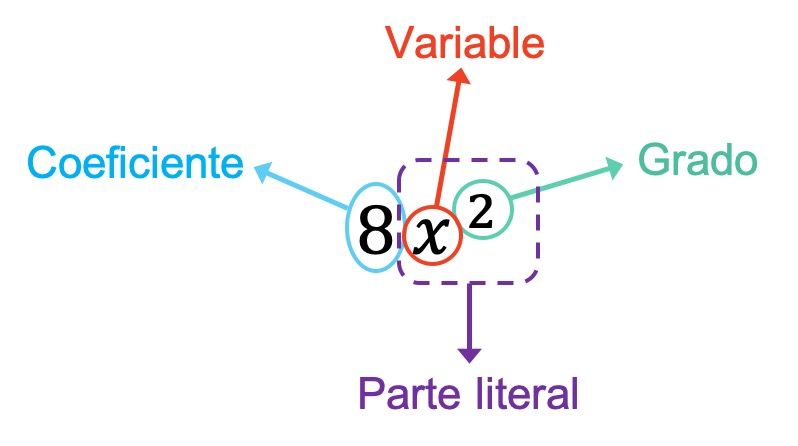
Zoals je in het vorige voorbeeld kunt zien, is de coëfficiënt van de monomial 8, omdat dit het getal is dat de variabelen vermenigvuldigt. Ook in dit geval heeft de monomial slechts één variabele, namelijk x. Daarom wordt het letterlijke deel van de monomial gevormd door deze variabele plus zijn exponent, namelijk x 2 . En ten slotte is de monomiaal van de tweede graad, omdat de enige exponent die hij heeft 2 is.
Aan de andere kant is een van de eigenschappen van de delen van een monomial dat wanneer twee monomials hetzelfde letterlijke deel hebben, er wordt gezegd dat ze vergelijkbare monomials zijn. Meer over dit soort monomialen kun je leren op de gelinkte pagina, waar onder andere wordt uitgelegd waarom ze zo belangrijk zijn voor de wiskunde.
Voorbeelden van delen van monomials
Zodat u het concept van delen van een monomial volledig begrijpt, laten we u verschillende voorbeelden achter:
voorbeeld 1
![]()
- Coëfficiënt van de monomial:
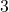
- Monomiale variabelen:
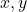
(in dit geval zijn er twee variabelen)
- Letterlijk deel van het monomial:
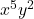
- Mate van het monomiaal:
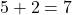
Voorbeeld 2
![]()
- Coëfficiënt van de monomial:
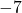
- Monomiale variabelen:
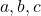
(in dit geval zijn er drie variabelen)
- Letterlijk deel van het monomial:
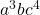
- Mate van het monomiaal:
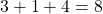
Houd er rekening mee dat wanneer de exponent van een variabele niet is ingesteld, dit betekent dat deze wordt verhoogd naar één en dat de exponent van die variabele in werkelijkheid dus 1 is en niet 0. Om deze reden hebben we een eenheid toegevoegd aan de berekening van de mate van dit monomiaal (3+ 1 +4=8), sindsdien
![]()
Als je meer geïnteresseerd bent, kun je op de volgende link meer voorbeelden van monomials zien. Bovendien kunt u zien welke verschillende soorten monomialen er bestaan, hoe de numerieke waarde van een monomial wordt berekend en wat het verschil is tussen een monomial en een polynoom.
Problemen opgelost met delen van monomials
Ten slotte bieden we je verschillende oefeningen aan, zodat je kunt controleren of je de verschillende definities van de onderdelen van een monomial hebt begrepen.
Oefening 1
Wat zijn alle onderdelen van de volgende monomial?
![]()
Coëfficiënt van de monomial:
![]()
Monomiale variabelen:
![]()
Letterlijk deel van het monomial:
![]()
Mate van het monomiaal:
![]()
Oefening 2
Identificeer alle elementen van de volgende monomial:
![]()
Coëfficiënt van de monomial:
![]()
Monomiale variabelen:
![]()
Letterlijk deel van het monomial:
![]()
Mate van het monomiaal:
![]()
Oefening 3
Bepaal de delen van de volgende monomiaal met een breuk:
![]()
Coëfficiënt van de monomial:
![]()
Monomiale variabelen:
![]()
Letterlijk deel van het monomial:
![]()
Mate van het monomiaal:
![]()
Perfect! Als je zo ver bent gekomen, begrijp je waarschijnlijk al alles over de onderdelen van een monomial. Daarom ben je klaar om het naar een hoger niveau te tillen en te leren hoe je operaties met monomials kunt uitvoeren . Hier zie je niet alleen hoe alle soorten bewerkingen met monomials die er bestaan worden berekend, maar zie je ook hoe je gecombineerde bewerkingen met monomials oplost en kun je stap voor stap oefenen met opgeloste oefeningen.