Op deze pagina vind je alles over loodrechte lijnen: wat ze zijn, wanneer twee lijnen loodrecht staan, hoe je een lijn loodrecht op een andere berekent, de eigenschappen ervan,… Daarnaast kun je voorbeelden zien en kun je oefenen met oefeningen die stap voor stap worden opgelost.
Wat zijn twee loodrechte lijnen?
In de wiskunde staan twee lijnen loodrecht wanneer ze elkaar snijden in een punt dat vier gelijke rechte hoeken vormt (90º).

Bovendien moeten de richtingsvectoren van twee loodrechte lijnen ook loodrecht zijn.
De loodrechtheid van twee lijnen wordt doorgaans aangegeven door het symbool
![]()
Onthoud daarentegen dat er in het vlak vier mogelijkheden zijn in het concept van de relatieve positie tussen twee lijnen: twee lijnen kunnen secans, loodrecht, samenvallend of evenwijdig zijn. Als u wilt, kunt u op onze website de betekenis van elk lijntype bekijken.
Hoe weet je of twee lijnen loodrecht staan?
Er zijn twee manieren om te bepalen wanneer twee lijnen loodrecht staan, op basis van hun richtingsvectoren of op basis van hun hellingen . Hieronder vindt u de uitleg van beide methoden. Hoewel ze hetzelfde doel dienen, raden we u aan te weten hoe u beide procedures moet uitvoeren, omdat elke procedure afhangt van hoe de lijnen worden uitgedrukt.
Van de richtingsvectoren van de lijnen
Eén manier om te weten of twee lijnen loodrecht staan, is door de richtingsvectoren van de betreffende lijnen te gebruiken. Onthoud dat de richtingsvector de vector is die de richting van een lijn aangeeft.
De richtingsvectoren van twee loodrechte lijnen zijn ook onderling orthogonaal. Als het puntproduct van de richtingsvectoren van twee lijnen gelijk is aan 0, betekent dit dat de lijnen loodrecht staan.
![]()
Laten we eens kijken hoe de loodrechtheid van twee lijnen wordt bepaald aan de hand van een voorbeeld:
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases} x=3-2t \\[2ex] y=6+3t \end{cases}\qquad \qquad s: \ \begin{cases} x=4+3t \\[2ex] y=-2+2t \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f8bad2c42aa92c183e085434ccb23cc2_l3.png)
Beide lijnen worden uitgedrukt als parametervergelijkingen, dus de componenten van de richtingsvector van elke lijn zijn de getallen vóór de parameter
![]()
![]()
Zodra we de richtingsvector van elke lijn kennen, controleren we of ze loodrecht staan door het product tussen de vectoren te berekenen:
![]()
Het puntproduct van de twee vectoren is nul, dus de lijnen staan loodrecht.
Lijn hellingen
Een andere manier om te bepalen of twee lijnen loodrecht staan, is door hun hellingen te gebruiken. Onthoud dat de helling van een lijn de coëfficiënt is
![]()
van de expliciete vergelijking en de punt-hellingsvergelijking van een lijn.
![]()
En de helling van een lijn kan ook uit de coëfficiënten worden afgeleid
![]()
En
![]()
van de impliciete (of algemene) vergelijking van een lijn:
![]()
De hellingen van twee loodrechte lijnen zijn dus omgekeerd en hebben een tegengesteld teken, dat wil zeggen dat er altijd aan de volgende gelijkheid wordt voldaan:
![]()
Dus als het product van de hellingen van twee verschillende lijnen gelijk is aan -1, betekent dit dat de lijnen loodrecht staan:
![]()
De volgende twee lijnen staan bijvoorbeeld loodrecht:
![]()
We kunnen aantonen dat het twee lijnen zijn die loodrecht op elkaar staan vanaf hun hellingen. De helling van elke lijn is:
![]()
Nu vermenigvuldigen we de hellingen:
![]()
Het product tussen de twee hellingen is gelijk aan -1, wat eigenlijk twee lijnen loodrecht op elkaar betekent.
Hoe bereken je een lijn loodrecht op een andere?
Hoewel het misschien moeilijk lijkt om te doen, is het vinden van een lijn loodrecht op een andere vrij eenvoudig. Hiervoor heb je alleen een richtingsvector nodig die loodrecht op de lijn staat en een punt dat bij de lijn hoort.
De enige moeilijkheid is dat de procedure, net als voorheen, afhangt van het type vergelijking waarin de lijnen worden uitgedrukt. Omdat een lijn loodrecht op een andere kan worden berekend op basis van de richtingsvectoren of op basis van de hellingen .
Vanuit de richtingsvector van rechts
Een lijn loodrecht op een andere gegeven lijn kan worden gevonden met behulp van zijn richtingsvector. Laten we eens kijken hoe dit wordt gedaan met een voorbeeld:
- Bereken de lijn loodrecht op de lijn

wat er door het punt gaat
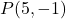
. eerlijk zijn

![]()
Het eerste dat we moeten doen is de richtingsvector van de lijn identificeren. In dit geval wordt de lijn gedefinieerd in de vorm van een algemene (of impliciete) vergelijking, daarom kunnen de cartesiaanse coördinaten van de richtingsvector van de lijn worden verkregen met de coëfficiënten A en B van de lijn:
![]()
En zodra we de richtingsvector van de lijn kennen, moeten we een vector loodrecht daarop berekenen. Om dit te doen, voegt u eenvoudigweg de coördinaten van de vector in en wijzigt u het teken van een ervan (degene die u wilt):
![]()
Dus nu kennen we de richtingsvector van de lijn. De impliciete vergelijking van de lijn zal daarom als volgt zijn:
![Rendered by QuickLaTeX.com \left.\begin{array}{c}\vv{\text{v}}= (-B,A) \\[2ex] \vv{\text{v}}_\perp= (3,2) \end{array} \right\}\longrightarrow \begin{array}{l}A=2 \\[2ex] B=-3 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7a24d8f41b3c82e25a2a64fed8dc6eb6_l3.png)
![]()
Daarom is het voldoende om de parameter C te bepalen. Om dit te doen, vervangen we het punt dat bij de rechte lijn hoort in de vergelijking en lossen we de resulterende vergelijking op:
![]()
![]()
![]()
![]()
![]()
Concluderend is de vergelijking van de loodrechte lijn:
![]()
Vanaf de helling van de lijn
Een andere manier om een lijn loodrecht op een bepaalde lijn te vinden, is vanaf de helling ervan. Laten we eens kijken hoe dit soort problemen wordt opgelost aan de hand van een voorbeeld:
- Bereken de lijn loodrecht op de lijn

wat er door het punt gaat
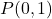
. eerlijk zijn

![]()
De helling van de lijn
![]()
Oosten:
![]()
Zodra we de helling van de lijn kennen, moeten we de helling van de loodrechte lijn vinden. Zoals we in de bovenstaande secties hebben gezien, zijn de hellingen van twee loodrechte lijnen omgekeerd en is hun teken veranderd. Om de helling van de loodrechte lijn te bepalen, moeten we daarom de gevonden helling omkeren en het teken ervan veranderen:
![]()
De expliciete vergelijking van de loodlijn zal daarom als volgt zijn:
![]()
![]()
Ten slotte berekenen we de ordinaat aan de oorsprong van de loodlijn door de coördinaten van het punt in de vergelijking van de lijn te vervangen:
![]()
![]()
![]()
Kort gezegd is de vergelijking van de loodrechte lijn:
![]()
Eigenschappen van loodrechte lijnen
Alle loodrechte lijnen hebben de volgende kenmerken:
- Symmetrische relatie : Als een lijn loodrecht staat op een andere lijn, staat die lijn ook loodrecht op de eerste lijn.
![]()
- Niet-reflexieve eigenschap : Het is duidelijk dat geen enkele lijn loodrecht op zichzelf kan staan.
![]()
- Stelling: In de Euclidische meetkunde (in R2) moet elk paar lijnen loodrecht op een derde lijn noodzakelijkerwijs evenwijdig zijn. Dat wil zeggen, als een lijn loodrecht staat op een andere lijn en die lijn staat ook loodrecht op een derde lijn, dan zijn de eerste en de laatste lijn evenwijdig.
Opgeloste problemen van loodrechte lijnen
Oefening 1
Welke van de volgende lijnen staan loodrecht op de lijn
![]()
?
![]()
![]()
![]()
![]()
![]()
De helling van de lijn
![]()
is 3:
![]()
En de hellingen van twee loodrechte lijnen zijn omgekeerd en hebben een tegengesteld teken, dus de helling van elke lijn loodrecht op de lijn
![]()
moet zijn:
![]()
Zodat de lijnen loodrecht op de lijn staan
![]()
zijn degenen waarvan de helling gelijk is aan
![]()
. Dat wil zeggen: de lijnen
![]()
En
![]()
Oefening 2
Bepaal of de volgende twee lijnen loodrecht staan:
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases} x=4-t \\[2ex] y=1-3t \end{cases}\qquad \qquad s: \ \cfrac{x-2}{4} = \cfrac{y+3}{6}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9e9d2323afa87c41dec84f29a4c5d645_l3.png)
het recht
![]()
wordt uitgedrukt in de vorm van een parametrische vergelijking, zodat de componenten van de richtingsvector van de genoemde lijn de getallen vóór de parameter zijn
![]()
![]()
Aan de andere kant, de rechte lijn
![]()
wordt gedefinieerd in de vorm van een continue vergelijking, dus de coördinaten van zijn richtingsvector zijn de getallen van de noemers:
![]()
Zodra we de richtingsvector van elke lijn kennen, kunnen we controleren of ze loodrecht staan door het product van de twee vectoren te berekenen:
![]()
Het puntproduct van de twee vectoren is niet nul, dus de lijnen staan niet loodrecht .
Oefening 3
Zoek de lijn loodrecht op de lijn
![]()
wat er door het punt gaat
![]()
. eerlijk zijn
![]()
![]()
Het eerste dat we moeten doen is de richtingsvector van de lijn identificeren. In dit geval wordt de lijn gedefinieerd in de vorm van een algemene (of impliciete) vergelijking, dus de richtingsvector is:
![]()
Zodra we de richtingsvector van de lijn kennen, moeten we een vector loodrecht daarop berekenen. Om dit te doen, voegt u eenvoudigweg de coördinaten van de vector in en wijzigt u het teken van een ervan (degene die u wilt):
![]()
De impliciete vergelijking van de lijn zal daarom als volgt zijn:
![Rendered by QuickLaTeX.com \left.\begin{array}{c}\vv{\text{v}}= (-B,A) \\[2ex] \vv{\text{v}}_\perp= (4,-1) \end{array} \right\}\longrightarrow \begin{array}{l}A=-1 \\[2ex] B=-4 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8833b30c014bab389b6df773ac4c4ea2_l3.png)
![]()
Het is daarom voldoende om de onbekende C te bepalen. Om dit te doen, vervangen we het punt waar de lijn doorheen gaat in de vergelijking:
![]()
![]()
![]()
![]()
![]()
Tenslotte is de vergelijking van de loodrechte lijn:
![]()
Oefening 4
Zoek de punt-hellingsvergelijking van de lijn loodrecht op de lijn
![]()
wat er door het punt gaat
![]()
. eerlijk zijn
![]()
![]()
De helling van de lijn
![]()
Oosten:
![]()
Zodra we de helling van de lijn kennen, moeten we de helling van de loodrechte lijn vinden. Om dit te doen, draait u eenvoudigweg de gevonden helling om en verandert u het teken:
![]()
Tenslotte vervangt u eenvoudigweg de gevonden helling en de coördinaten van het punt in de punt-hellingsvergelijking van de lijn:
![]()
![]()
![]()
Oefening 5
het recht
![]()
gaat door de punten (2,1) en (4,2) en de lijn
![]()
gaat door de punten (-1,2) en (1,-2). Bepaal of dit twee loodrechte lijnen zijn of niet.
Om te controleren of dit twee loodrechte lijnen zijn, berekenen we hun hellingen en kijken we of ze de loodrechte relatie respecteren. Onthoud dat de formule voor de helling van een lijn is:
![]()
De helling van de lijn
![]()
Oosten:
![]()
De helling van de lijn
![]()
Oosten:
![]()
Om de loodrechtheid van de twee lijnen te controleren, moeten we kijken of de helling van de ene lijn het omgekeerde is van de andere helling. In dit geval zijn de twee hellingen omgekeerd en hebben ze ook tegengestelde tekens, zodat de twee lijnen loodrecht op elkaar staan.
Oefening 6
Bereken de waarde van
![]()
zodat de volgende twee lijnen loodrecht staan:
![]()
De twee lijnen worden uitgedrukt in de vorm van een impliciete (of algemene) vergelijking, en de richtingsvector van een impliciete vergelijking van de lijn is:
![]()
![]()
Daarom zou de richtingsvector van elke lijn zijn:
![]()
Om twee lijnen loodrecht te laten staan, moet het scalaire product van hun richtingsvectoren nul zijn. Daarom zullen we deze voorwaarde toepassen om de waarde van het onbekende te vinden
![]()
![]()
![]()
![]()
![]()
![]()
![]()