Parallelle lijnen - Mathority

Hier vindt u alles over parallelle lijnen: wat ze betekenen, hoe u kunt bepalen of twee lijnen evenwijdig zijn, hun eigenschappen, enz. Daarnaast kun je verschillende voorbeelden en opgeloste oefeningen van parallelle lijnen zien.

Wat zijn parallelle lijnen?

Parallelle lijnen zijn die lijnen die elkaar nooit kruisen, dat wil zeggen: zelfs als hun trajecten zich tot in het oneindige uitstrekken, raken ze elkaar nooit. Daarom liggen de punten van twee parallelle lijnen altijd op dezelfde afstand van elkaar en bovendien hebben twee parallelle lijnen geen gemeenschappelijke punten.

De volgende twee lijnen zijn bijvoorbeeld evenwijdig:

Over het algemeen geven we aan dat twee lijnen evenwijdig zijn met 2 verticale balken || tussen de lijnen

Aan de andere kant zeggen we, ondanks het feit dat twee evenwijdige lijnen elkaar nooit snijden, in de analytische meetkunde dat ze een hoek van 0° vormen, omdat ze dezelfde richting hebben.

Wanneer zijn twee lijnen evenwijdig?

Zodra we de definitie van parallelle lijnen hebben gezien, zullen we zien hoe we twee parallelle lijnen kunnen vinden. Eén manier zou uiteraard zijn om de lijnen in een grafiek weer te geven en te kijken of ze elkaar in de grafiek snijden, maar er zijn nog eenvoudiger en gemakkelijker te gebruiken methoden.

Bepaal de parallelliteit van twee lijnen met hun hellingen

Je kunt zien of twee lijnen evenwijdig zijn door naar de helling van elke lijn te kijken. Onthoud dat de helling van een lijn de parameter is

$m$

uit de expliciete vergelijking en de punt-hellingsvergelijking van de lijn:

$y=mx+n \qquad \qquad y-y_0=m(x-x_0)$

Er zijn echter verschillende manieren om de helling van een lijn te bepalen. Om erachter te komen hoe je deze kunt berekenen, raden we je aan de formule voor de helling van een lijn te bekijken. Daarnaast vindt u op de gelinkte pagina ook uitleg over wat de helling van een lijn voorstelt en waarom deze zo belangrijk is voor een lijn.

In het vlak zijn dus twee lijnen evenwijdig als ze dezelfde helling (coëfficiënt m) en verschillende ordinaten hebben bij de oorsprong (coëfficiënt n) .

De volgende twee lijnen zijn bijvoorbeeld evenwijdig:

$r: \ y=5x+1 \qquad \qquad s: \ y=5x-3$

Het zijn twee parallelle lijnen omdat ze allebei dezelfde helling hebben en bovendien hun onafhankelijke termen verschillend zijn.

$m_r =m_s =5$

$n_r =1 \neq n_s =-3$

Opgemerkt moet worden dat als twee lijnen dezelfde helling hadden en tegelijkertijd dezelfde computer in de oorsprong, het identieke lijnen zouden zijn omdat ze exact identiek zouden zijn.

Zoek de parallelliteit van twee lijnen uit de impliciete vergelijking

Onthoud dat de impliciete (of algemene) vergelijking van de lijn is:

$Ax+By+C=0$

Dus als de coëfficiënten A en B van twee lijnen evenredig zijn met elkaar, maar niet met de coëfficiënt C , betekent dit dat de lijnen evenwijdig zijn.

$r: \ Ax+By+C=0 \qquad \qquad s: \ A'x+B'y+C'=0$

$\cfrac{A}{A'} = \cfrac{B}{B'} \neq \cfrac{C}{C'} \quad \bm{\longrightarrow} \quad r \parallel s$

Hier zijn twee parallelle lijnen uitgedrukt in algemene (of impliciete) vergelijkingsvorm:

$r: \ 4x-6y+7=0 \qquad \qquad s: \ -2x+3y-1=0$

Ze zijn parallel omdat de getallen vóór de variabele staan

$x$

zijn evenredig met de getallen vóór de variabele

$y$

, maar niet met onafhankelijke termen.

$\cfrac{4}{-2} = \cfrac{-6}{3} = -2 \neq \cfrac{7}{-1}=-7$

Als alle coëfficiënten (A, B en C) van twee impliciete lijnen evenredig zouden zijn, zou dit, net als voorheen, impliceren dat de twee lijnen samenvallen, of met andere woorden, dat ze gelijk zijn.

Eigenschappen van parallelle lijnen

De kenmerken van parallelle lijnen zijn als volgt:

Symmetrische eigenschap : als de ene lijn evenwijdig is aan de andere, is deze lijn ook evenwijdig aan de eerste. Deze eigenschap wordt ook bezeten door loodrechte lijnen.

$r \parallel s \ \longrightarrow \ s \parallel r$

Transitieve eigenschap : als een lijn evenwijdig is aan een andere lijn, en deze tweede lijn is evenwijdig aan een derde lijn, dan is de eerste lijn ook evenwijdig aan de derde lijn.

$\left. \begin{array}{c} r \parallel s\\[2ex] s \parallel q \end{array} \right\} \longrightarrow \ r \parallel q$

Het scalaire product van de richtingsvectoren (vector die de richting van een lijn aangeeft) van twee parallelle lijnen is gelijk aan het product van hun modules.

$r \parallel s \ \longrightarrow \ \vv{\text{v}}_r \cdot \vv{\text{v}}_s= \lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{\text{v}}_s \rvert$

Bovendien zijn de richtingsvectoren van twee parallelle lijnen altijd lineair van elkaar afhankelijk, aangezien ze proportioneel zijn.

Deze voorwaarde is nodig om lijnen evenwijdig te laten zijn, maar is niet voldoende, of met andere woorden: twee parallelle lijnen moeten proportionele richtingsvectoren hebben, maar het feit dat twee lijnen proportionele richtingsvectoren hebben, impliceert niet direct dat ze evenwijdig zijn. Omdat samenvallende lijnen ook proportionele richtingsvectoren hebben.

Lijnen evenwijdig aan de abscis-as (X-as) zijn horizontaal en hebben altijd de vorm
$y=k.$

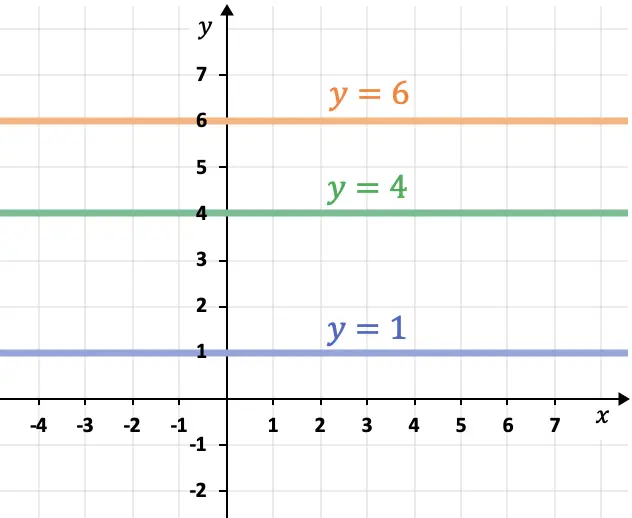
Lijnen evenwijdig aan de computeras (Y-as) zijn verticaal en volgen altijd de uitdrukking
$x=k.$

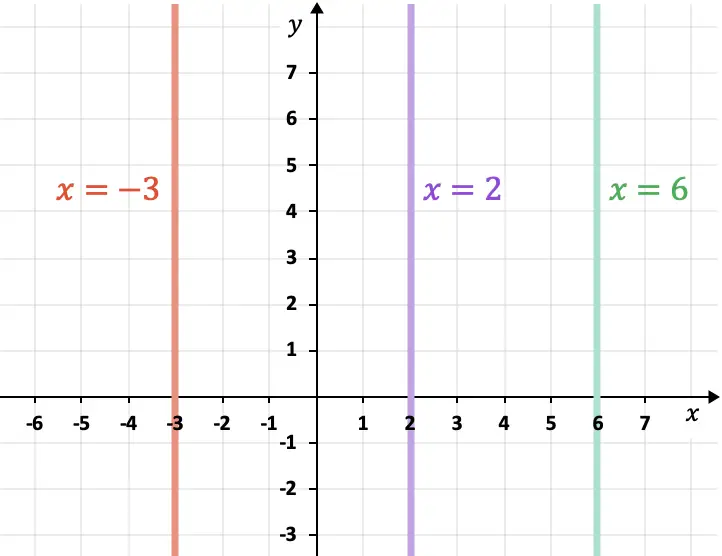
Hoe de afstand tussen twee evenwijdige lijnen in het vlak te berekenen

Om de afstand tussen twee parallelle lijnen in het vlak (in R2) te vinden, neemt u eenvoudigweg een punt op een van de twee lijnen en berekent u de afstand vanaf dit punt tot de andere lijn.

We kunnen het op deze manier doen omdat twee parallelle lijnen altijd op dezelfde afstand van elkaar liggen.

Aan de andere kant, als we bij het gebruik van de formule een afstand van 0 eenheden krijgen, betekent dit dat de lijnen elkaar op een bepaald punt raken en dat de lijnen daarom niet evenwijdig zijn, maar elkaar snijden, samenvallen of loodrecht staan. Als je wilt, kun je op onze website de verschillen tussen dit soort lijnen bekijken.

Om u te laten zien hoe dit wordt gedaan, bepalen we als voorbeeld de afstand tussen de volgende twee parallelle lijnen:

$r: \ 2x-4y-6=0 \qquad \qquad s: \ -x+2y+4=0$

Het eerste wat we moeten doen is een punt op een van de lijnen krijgen (degene die je wilt). In dit geval berekenen we een punt op de lijn

$s.$

Om dit te doen, moeten we een waarde toekennen aan een van de variabelen, wat we bijvoorbeeld zullen doen

$x=0:$

$-x+2y+4 =0 \ \xrightarrow{x \ = \ 0} \ -0+2y+4=0$

En nu wissen we de andere variabele (

$y$

) van de verkregen vergelijking om te weten hoeveel het op dit punt waard is:

$2y=-4$

$y= \cfrac{-4}{2}$

$y= -2$

Daarom wordt het punt verkregen uit de lijn

$s$

Oosten:

$P(0,-2)$

En zodra we al een punt op een lijn hebben, berekenen we de afstand van dat punt tot de andere lijn met behulp van de formule voor de afstand van een punt tot een lijn:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

$d(P,r)= \cfrac{\lvert 2\cdot 0 + (-4)\cdot (-2) +(-6)\rvert}{\sqrt{2^2+(-4)^2}}= \cfrac{\lvert 0+8-6\rvert}{\sqrt{4+16}}={\cfrac{2}{\sqrt{20}}=\bm{0,45}$

De afstand tussen de twee evenwijdige lijnen is dus gelijk aan 0,45 eenheden .

Parallelle lijnen opgeloste problemen

Oefening 1

Welke van de volgende lijnen zijn evenwijdig?

$\begin{array}{l} r: \ y=2x+3 \\[2ex] s: \ y=3x-2 \\[2ex] q: \ y=2x+6 \\[2ex] t: \ y=-2x-4\end{array}$

zie oplossing

Twee lijnen zijn evenwijdig als ze dezelfde helling hebben (en verschillende snijpunten). De helling van elke lijn is dus:

$m_r = 2$

$m_s = 3$

$m_q = 2$

$m_t = -2$

Dus alleen de lijnen zijn evenwijdig

$r$

$q,$

omdat zij de enigen zijn met gelijke hellingen.

Oefening 2

Zoek de expliciete vergelijking van de lijn evenwijdig aan de lijn

$r$

en wat er aan de overkant gebeurt

$P(0,2).$

eerlijk zijn

$r:$

$r: \; y=3x-1$

zie oplossing

Zodat de lijn evenwijdig is aan de lijn

$r,$

beide moeten dezelfde helling hebben. en de helling van de lijn

$r$

is 3:

$m = 3$

Daarom is de expliciete vergelijking van de lijn die we moeten vinden:

$y=3x+n$

En zodra we de helling van de lijn kennen, kunnen we het snijpunt berekenen door het punt dat bij de lijn hoort in de vergelijking van de lijn te vervangen:

$P(0,2)$

$y= 3x+n \ \xrightarrow{x=0 \ ; \ y=2} \ 2=3\cdot 0 +n$

$2=0+ n$

$2= n$

Dus de expliciete vergelijking van de lijn is:

$\bm{y=3x+2}$

Oefening 3

Bereken de waarde van de onbekenden

$a$

$b$

zodat de volgende twee lijnen evenwijdig zijn:

$r: \ 2x-4y+6=0 \qquad \qquad s: \ x+ay+b=0$

zie oplossing

De lijnen worden beschreven in algemene (of impliciete) vergelijkingsvorm. Om de twee lijnen evenwijdig te laten zijn, moeten hun coëfficiënten A en B daarom proportioneel zijn, dat wil zeggen dat aan de volgende vergelijking moet worden voldaan:

$\cfrac{2}{1} = \cfrac{-4}{a}$