Decimale getallen zijn van groot belang in de wiskundige wereld, maar weten we echt wat ze zijn en hoe ze werken? In dit artikel leggen wij je alles uit.
Wat zijn decimale getallen?
Decimale getallen zijn niet-gehele getallen (niet opgenomen in de gehele verzameling ), met een geheel getal en een decimaal gedeelte. Dit decimale deel wordt na een komma geschreven en maakt het mogelijk waarden kleiner dan één uit te drukken.
Decimale getallen zijn een manier om gemengde getallen weer te geven. Het concept van breuk lijkt inderdaad behoorlijk op dat van decimale waarde. We kunnen dit zien in het volgende voorbeeld: 7/2 is gelijk aan 3,5 . Ze behouden de numerieke gelijkwaardigheid, alleen dat ze anders zijn geschreven.
Het getal “3,5” is een decimaal getal dat luidt als “drie komma vijf”, het gehele deel is 3 en het decimale deel is gelijk aan 5. Omdat decimale getallen worden uitgedrukt met behulp van het decimale notatiesysteem, kunnen we het getal als volgt ontleden :
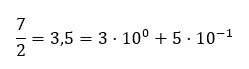
decimale nomenclatuur
Bij het schrijven van deze getallen worden vaak twee soorten notatie gebruikt: standaardnotatie (of decimale notatie) en wetenschappelijke notatie . Deze eerste is de meest voorkomende en is degene die we tot nu toe hebben gebruikt.
Terwijl wetenschappelijke notatie een verkorte vorm van standaardnotatie is. In de wetenschappelijke notatie wordt een decimaal getal geschreven als een geheel getal vermenigvuldigd met een macht van 10 . De grootheid 0,0054 kan bijvoorbeeld in wetenschappelijke notatie worden geschreven als 5,4 · 10 -3 .
Wat het niet-numerieke schrijven van decimalen betreft, gebruiken we een notatie die verwijst naar de positie die elk decimaal cijfer inneemt. Nou ja, net zoals het gehele deel heeft: de eenheid, de tien, de honderd… Het decimale deel heeft: de tiende, de honderdste, de duizendste…
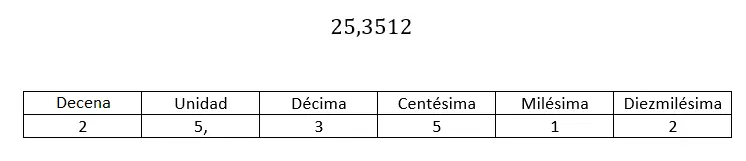
Wat de naam van elk cijfer markeert, is de positie die het inneemt ten opzichte van de komma . Op deze manier moet je, als je een decimaal getal hebt en je wilt weten wat de waarde van de honderdste is, naar het tweede cijfer kijken (vanaf de komma naar rechts). In het bovenstaande geval is de honderdste gelijk aan 5.
soorten decimalen
Decimale getallen kunnen als volgt worden geclassificeerd:
- Exact decimaal: heeft een bepaald en eindig aantal decimalen. Bijvoorbeeld: 9.263.
- Herhalend decimaal: heeft een oneindig aantal decimalen.
- Zuiver herhalend decimaal: het decimale deel bestaat uit een getal dat zich oneindig herhaalt. Bijvoorbeeld: 2.1515151515… Sinds 15 herhalingen voor onbepaalde tijd.
- Gemengd herhalend decimaal: het decimale deel bestaat uit een waarde, gevolgd door een ander getal dat oneindig wordt herhaald. Bijvoorbeeld: 2.4615151515… Omdat 46 niet wordt herhaald.
- Niet-herhalend decimaal: heeft een oneindig decimaal deel, dat niet wordt herhaald. In deze sectie vinden we enkelewiskundige constanten , de vierkantswortel van twee…

Eigenschappen van decimale getallen
Decimale getallen hebben verschillende eigenschappen, waaronder:
- Een decimaal verandert niet als er rechts nullen worden toegevoegd, dus het getal 0,25 is gelijk aan 0,250 en 0,2500. Kortom, omdat ze hetzelfde bedrag uitdrukken.
- Decimalen zijn gelijk aan breuken, een halve eenheid (1/2) wordt bijvoorbeeld weergegeven door 0,5.
- Als we een decimaal getal vermenigvuldigen of delen met machten van tien, moeten we de komma verplaatsen: naar rechts als we vermenigvuldigen en naar links als we delen.
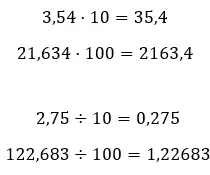
- Een decimaal getal kun je vereenvoudigen, dit doe je door de decimale getallen af te ronden . Deze methode bestaat uit het uitdrukken van minder decimale cijfers, waarbij de waarde van het getal zo min mogelijk wordt gewijzigd. Als u wilt leren hoe u dit vereenvoudigingssysteem kunt gebruiken, raden wij u aan deze laatste link in te voeren.
Weergave van decimale getallen
De decimale set kan net als alle andere sets op de getallenlijn worden weergegeven.
Uitgaande van het feit dat decimalen een geheel getal en een decimale plaats (minder dan één) hebben, kunnen we afleiden dat decimalen tussen gehele getallen worden weergegeven. Tussen het getal 0 en 1 bevinden zich bijvoorbeeld oneindig veel cijfers achter de komma. Hieronder zie je het weergegeven in de regel:
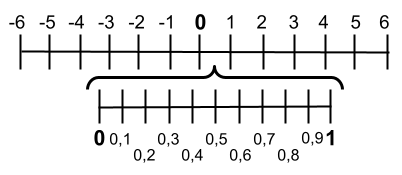
Zoals je in de afbeelding kunt zien, hebben we de tienden tussen 0 en 1 geschreven. Hoewel er tussen deze twee getallen oneindig veel cijfers achter de komma staan , kunnen er zeer complexe representaties worden gemaakt. En bovendien gebeurt dit niet alleen tussen 0 en 1, maar tussen alle gehele getallen.
Bewerkingen op decimale getallen
De bewerkingen van decimale getallen zijn vergelijkbaar met die van gehele getallen. Het enige verschil is dat er rekening moet worden gehouden met de decimale cijferposities. Voordat u een bewerking oplost, moet u er daarom voor zorgen dat u altijd met dezelfde getallen werkt: tienden met tienden, honderdsten met honderdsten…
Vervolgens zullen we een kort overzicht geven van de vier elementaire rekenkundige bewerkingen met decimalen:
- Optelling van decimalen:

- Aftrekken van decimale getallen:

- Vermenigvuldiging van decimalen:

- Decimale deling:

Gebruik en toepassingen van decimale getallen
Decimale getallen worden veel gebruikt in het dagelijks leven en in de wiskunde. Wanneer u bijvoorbeeld iets in een winkel koopt , moet u de prijs weten van wat u koopt, en die prijs wordt uitgedrukt in decimale getallen. Bovendien worden ze gebruikt om afstanden, gewichten en andere aspecten van het dagelijks leven te meten.
In de wiskunde stellen decimale getallen ons in staat om gemakkelijk zeer kleine of zeer grote hoeveelheden uit te drukken. En ze stellen ons ook in staat om berekeningen met grotere nauwkeurigheid te maken. Als we bijvoorbeeld de helft van 3 eenheden willen berekenen, kunnen we deze in twee gelijke delen verdelen en 1,5 eenheden krijgen.