Stelling van Weierstrass

In dit artikel vind je de definitie van de stelling van Weierstrass. Bovendien kun je oefenen met verschillende oefeningen die stap voor stap zijn opgelost met de stelling van Weierstrass om deze perfect te begrijpen.

Verklaring van de stelling van Weierstrass

De stelling van Weierstrass zegt dat als een functie continu is op een gesloten interval, die functie een absoluut maximum en een absoluut minimum heeft op dat interval.

➤ Zie: Wat is een continue functie?

De stelling van Weierstrass stelt alleen dat er een maximum en een minimum is, maar het heeft geen zin om de waarden van deze punten te berekenen.

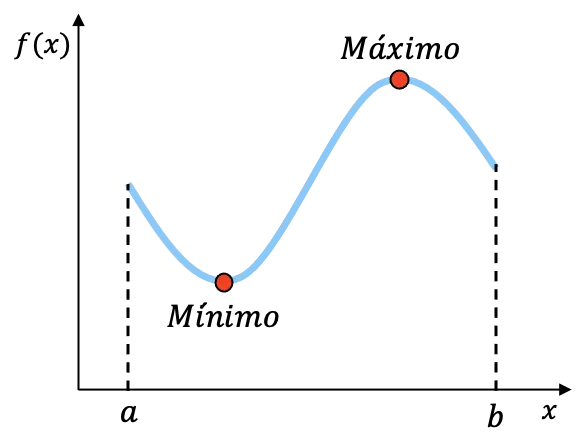
De hierboven weergegeven functie is bijvoorbeeld continu op het interval [a,b] en heeft een minimum en een maximum op dit interval. Hoewel we de exacte coördinaten van deze twee punten niet kunnen weten, weten we dat de functie deze twee eindpunten in het interval heeft.

➤ Zie: hoe je het maximum en minimum van een functie berekent

Omdat de functie continu is over het gehele interval, betekent dit dat deze over datzelfde interval ook alle mogelijke waarden tussen het absolute minimum en het absolute maximum zal aannemen.

Bovendien kan men, als gevolg van de stelling van Weierstrass, afleiden dat elke continue functie op een gesloten interval boven en onder begrensd is, en dat de boven- en ondergrenzen van de functie respectievelijk het absolute maximum en minimum zijn.

Wiskundig gezien kan de stelling van Weierstrass als volgt worden uitgedrukt:

$f(x_1)\leq f(x)\leq f(x_2)$

Goud

$x_1$

$x_2$

zijn twee opgenomen punten (respectievelijk het absolute minimum en het absolute maximum) in het gesloten interval

$[a,b]$

waarin de functie is gedefinieerd.

Het bewijs van de stelling van Weierstrass is behoorlijk ingewikkeld en draagt niet veel bij aan het concept, dus we zullen het in dit artikel niet uitleggen. Het belangrijkste is dat je begrijpt wat de stelling van Weierstrass is en waarvoor deze wordt gebruikt.

Stelling van Weierstrass opgeloste problemen

Oefening 1

Bepaal of de volgende functie begrensd is op het voorgestelde interval:

$f(x)=\log_3(x-4) \qquad x \in [5,10]$

➤ Zie: domein van een logaritmische functie

zie oplossing

We kunnen bepalen of de functie wordt begrensd op het interval [5,10] door de stelling van Weierstrass toe te passen. We moeten daarom weten of de functie continu is in dit interval. Om dit te doen, berekenen we het domein van de logaritmische functie:

$x-4>0″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”73″ style=”vertical-align: -2px;”> 4″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”43″ style=”vertical-align: -2px;”> <p class=$ $\text{Dom } f = (4,+\infty)$

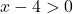
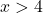
De functie is continu voor alle waarden groter dan x=4, dus continu op het interval [5,10].

Daarom voldoet de functie aan de stelling van Weierstrass over het interval [5,10], wat betekent dat deze op dit interval boven en onder begrensd is.

Oefening 2

Bepaal of de volgende functie een maximum en/of minimum heeft over het voorgestelde interval:

$f(x)=\cfrac{3x^2-4}{2x-4} \qquad x \in [-3,3]$

➤ Zie: domein van een rationale functie

zie oplossing

Eerst analyseren we de continuïteit van de rationele functie:

$2x-4=0$

$2x=4$

$x=\cfrac{4}{2}=2$

$\text{Dom } f = \mathbb{R}- \{ 2\}$

De functie vertoont echter een discontinuïteit bij x=2, wat impliceert dat deze niet continu is op het interval [-3,3].

Kortom, de functie voldoet niet aan de stelling van Weierstrass en daarom kunnen we niet zeggen of deze een minimum of maximum heeft in dit interval.

Oefening 3

Bepaal of de volgende functie een maximum en/of minimum heeft in het voorgestelde interval en bereken deze punten:

$f(x)=x^2+3 \qquad x \in [0,4]$

➤ Zie: kenmerken van kwadratische functies

zie oplossing

Het domein van elke kwadratische functie bestaat uit alle reële getallen:

$\text{Dom } f=\mathbb{R}$

De functie is daarom continu op het interval [0,4] en voldoet aan de stelling van Weierstrass. De functie heeft dus een absoluut minimum en een absoluut maximum op dit interval.

Bovendien ligt het hoekpunt van deze parabool precies op x=0, dus de functie neemt strikt toe op het interval [0,4] en bijgevolg ligt het minimum op x=0 en het maximum op x= 4 .

$\text{M\'inimo en } x=0 \ \longrightarrow \ f(0)=0^2+3=3$

$\text{M\'aximo en } x=4 \ \longrightarrow \ f(4)=4^2+3=19$

Karl Weierstrass

Nadat we hebben gezien wat de stelling van Weierstrass betekent, zullen we kort uitleggen wie de inventaris van deze stelling was.

Karl Theodor Wilhelm Weierstrass was een zeer belangrijke Duitse wiskundige in de 19e eeuw, meer precies, hij werd geboren op 31 oktober 1815 in Ostenfelde en stierf op 19 februari 1897 in Berlijn.

Naast de stelling van Weierstrass staat hij ook bekend om zijn andere bijdragen aan de wiskunde. Onder hen gaf hij de definities van continuïteit, limiet en afgeleide, drie zeer belangrijke concepten van functies.

Op dezelfde manier slaagde hij erin bepaalde stellingen aan te tonen die op dat moment nog niet wiskundig geverifieerd waren, zoals de stelling van Bolzano-Weierstrass, de stelling van de gemiddelde waarde of de stelling van Heine-Borel.

Uit nieuwsgierigheid is er een maankrater en een asteroïde die ter ere van hem naar Weierstrass is vernoemd.

De stelling van weierstrass

Verklaring van de stelling van Weierstrass

Stelling van Weierstrass opgeloste problemen

Oefening 1

Oefening 2

Oefening 3

Karl Weierstrass

Laat een reactie achter Reactie annuleren