De binomiaal van Newton is een wiskundige formule die wordt gebruikt om de som uit te drukken van twee termen verheven tot een bepaalde macht . Deze formule, genoemd naar de Britse wiskundige Isaac Newton, wordt op veel gebieden van de wiskunde gebruikt.
Het is bijvoorbeeld bruikbaar in de statistiek, de kansrekening en de differentiaal- en integraalrekening. Met de binominale stelling kunnen we op een eenvoudige manier de macht van een binominale berekening berekenen.
Simpel gezegd is de binomiaal van Newton gebaseerd op een formule waarmee elke algebraïsche uitdrukking van de vorm (a+b) n kan worden opgelost. Ondanks het feit dat deze formule naar Isaac Newton is vernoemd, is het vermeldenswaard dat er controverse bestaat over de oorsprong ervan.
Dat wil zeggen, sommige onderzoeken suggereren dat het gebruik van de binominale stelling in het Midden-Oosten wordt gevonden.
Wanneer werd de binomiaal van Newton ontwikkeld?
De binominale stelling van Newton, ook bekend als de binominale stelling van Newton, werd ontwikkeld in 1665 en voor het eerst gecommuniceerd in twee brieven van de officier van de Royal Society in 1676 .
Deze brieven waren een reactie op de Duitse wiskundige Gottfried Wilhelm von Leibniz, die wiskundig onderzoek naar oneindige reeksen beter wilde begrijpen. Newton deelde de resultaten van zijn stelling en Leibniz erkende dat het een nuttige techniek was om resultaten in kwadratuur of reeksen te verkrijgen.
Deze observatie stelde Newton in staat te concluderen dat het mogelijk was om op dezelfde manier met oneindige reeksen te werken als met eindige polynoomuitdrukkingen . Hoewel Newton zijn stelling nooit publiceerde, publiceerde de Britse wiskundige John Wallis deze in 1685 in zijn Algebra en schreef de creatie ervan toe aan Newton.
Waarom wordt het de binomiaal van Newton genoemd?
De binomiaal van Newton is vernoemd naar de Engelse wiskundige en natuurkundige Isaac Newton, die deze in de 17e eeuw ontwikkelde . Newton was niet de eerste die deze stelling ontdekte, maar hij was wel de eerste die de geldigheid ervan bewees voor elk positief geheel getal n.
De binomiaal van Newton is een zeer nuttig wiskundig hulpmiddel in de algebra en calculus, en wordt veel gebruikt op gebieden als natuurkunde, statistiek, techniek en informatica.
Wat is de binomiale formule van Newton?
Zoals we eerder vermeldden, is de binomiaal van Newton de formule waarmee de machten van een binomiaal kunnen worden gevonden . Om deze binominale macht te vinden, worden “binomiale coëfficiënten” gebruikt. De vorige term verwijst naar reeksen combinaties.
Met dit in gedachten kunnen we de binomiale formules van Newton als volgt opsplitsen:
- (a + b) 2 = a 2 + 2ab + b 2
- (a – b) 2 = a 2 – 2ab + b 2
- (a + b) 3 = een 3 + 3a 2 b + 3 ab 2 + b 3
De wiskundige uitdrukkingen die verwijzen naar de ontwikkeling van (a+b) n worden opmerkelijke entiteiten genoemd en maken het mogelijk een algemene formule te verkrijgen die deze bewerking voor elk natuurlijk getal “n” weergeeft.
Door de coëfficiënten van elke resulterende polynoom te onderzoeken, kunnen we een reeks opmerken die volgt op wat bekend staat als de driehoek van Pascal .
De reeks van de driehoek van Pascal begint met het getal 1, en in elke volgende regel zijn de laatste cijfers altijd 1. Tussenwaarden worden verkregen door de twee getallen uit de vorige regel op te tellen die direct boven de te berekenen waarde liggen.
Hoe vind je een term in de binomiaal van Newton?
Om een specifieke term in de binominale term van Newton te vinden, wordt de algemene formule gebruikt:
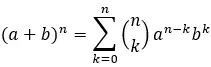
Goud:
a en b zijn de coëfficiënten van de binominale waarde.
n is de exponent van de binominale waarde.
k is de specifieke term die we willen vinden.
Σ vertegenwoordigt de som van k=0 tot n.
[nk] is de binominale coëfficiënt berekend met de volgende formule:
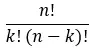
Daarom is de volledig uitgebreide formule zodanig dat:
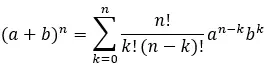
Voorbeeld van een Newton-binomiaal opgelost
Zodra deze waarden zijn gevonden, worden ze in de formule vervangen en wordt de uitdrukking opgelost om de specifieke term te verkrijgen. Als we bijvoorbeeld de vijfde term van de binomiale (2x + 3) 6 zouden willen vinden, zouden we:
één = 2x
b = 3
n=6
k = 5
Dus met behulp van de formule:
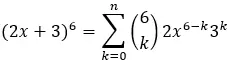
De vijfde term komt overeen met k=5, we hebben dus:
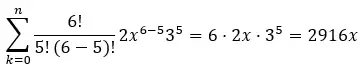
Daarom is de vijfde term van de binomiale (2x + 3) 6 2916x.
Wat is een Newton-binomiaal van graad 5?
Een Newton-binomiaal van graad 5 is een algebraïsche uitdrukking van de vorm (a + b) 5 , waarbij “a” en “b” variabelen zijn en de exponent 5 de graad van de binominale waarde aangeeft . Als we deze uitdrukking uitbreiden, verkrijgen we een kwadratische polynoom die zes termen heeft:
(a + b) 5 = a 5 + 5a 4 b + 10a 3 b 2 + 10a 2 b 3 + 5ab 4 + b 5
Elke term van dit polynoom wordt verkregen door de coëfficiënten van de binominale waarde te combineren met de machten van “a” en “b”. De tweede term (5a 4 b) wordt bijvoorbeeld verkregen door de binominale coëfficiënt (5 kies 1 = 5) te vermenigvuldigen met “a” tot de vierde macht en met b tot de eerste macht.
Newtons binomialen van graad 5 zijn bruikbaar in verschillende takken van de wiskunde en natuurkunde, zoals statistiek, waarschijnlijkheidstheorie en kwantummechanica.
Wat zijn de toepassingen van de binomiaal van Newton?
De binomiaal van Newton heeft een grote verscheidenheid aan toepassingen op verschillende gebieden, waaronder:
- Waarschijnlijkheden berekenen : De binominale stelling wordt gebruikt om de waarschijnlijkheden van binomiale gebeurtenissen te berekenen , zoals het opgooien van een munt of het slagen of mislukken van een reeks tests.
- Getaltheorie – De binominale waarde van Newton wordt gebruikt om polynomen uit te breiden en vergelijkingen in de getaltheorie te vereenvoudigen.
- Statistieken : De binomiale waarde van Newton wordt gebruikt om binominale verdelingen te berekenen en bij de constructie van betrouwbaarheidsintervallen.
- Natuurkunde – In de natuurkunde wordt de binominale stelling onder meer gebruikt in de relativiteitstheorie en de kwantummechanica.
- Economie en Financiën : De binominale waarde van Newton wordt gebruikt om de huidige en toekomstige waarde van kasstromen in de loop van de tijd te berekenen en bij de waardering van financiële opties.
- Programmeren en informatica : De binominale waarde van Newton wordt gebruikt bij de ontwikkeling van algoritmen en bij het programmeren van computers.
Waarom is de binominale waarde van Newton belangrijk?
De binomiaal van Newton is relevant omdat het een fundamenteel wiskundig hulpmiddel is voor de ontwikkeling van algebra en getaltheorie . Hiermee kunt u het resultaat van het kwadrateren of een andere macht van een binominale berekening berekenen, wat erg handig is voor het oplossen van vergelijkingen en het vereenvoudigen van algebraïsche uitdrukkingen.
Bovendien heeft het toepassingen op gebieden als onder meer statistiek, waarschijnlijkheid en natuurkunde . Samenvattend is de binomiaal van Newton een essentieel concept in de wiskunde en het begrijpen ervan is cruciaal om vooruitgang te boeken in veel vakgebieden.
Zijn er andere manieren om de binomiaal van Newton uit te drukken?
Ja, er zijn andere manieren om de binomiaal van Newton uit te drukken. Het kan bijvoorbeeld worden uitgedrukt in termen van binominale coëfficiënten met behulp van combinatorische notatie.
Bovendien kan het worden uitgedrukt in termen van exponentiële functies en trigonometrische functies met behulp van de formule van Euler. Op dezelfde manier in termen van gammafunctie met behulp van de formule van Legendre. Deze alternatieve uitdrukkingen kunnen nuttig zijn in verschillende contexten en wiskundige problemen.
Binominale voorbeelden van Newton
Laten we dan enkele eenvoudige voorbeelden bekijken van de toepassing van de binomiaal van Newton.
Voorbeeld 1: Bereken de term van orde 3 in de uitbreiding van (x + y) 5 .
Oplossing: Bij de uitbreiding van (x + y) 5 is de coëfficiënt van de eerste term 1, de coëfficiënt van de tweede term is 5, de coëfficiënt van de derde term is 10, de coëfficiënt van de vierde term is 10, de De coëfficiënt van de vijfde term is 5 en de coëfficiënt van de zesde term is 1.
De looptijd van opdracht 3 is daarom:
10x 2 en 3
Voorbeeld 2: Zoek de onafhankelijke term in de uitbreiding van (2x – 1) 4 .
Oplossing: Bij de uitbreiding van (2x – 1) 4 wordt de onafhankelijke term gevonden in de combinatie (2x) p (-1) (4-p) , waarbij p de waarde is die de exponent van (2x) p maakt en (-1) (4-p) optellen is 4.
De onafhankelijke term is daarom:
(2x) 2 (-1) 2 = 4
Voorbeeld 3: Vind de term met de hoogste graad in de uitbreiding van (3x – 2y) 6 .
Oplossing: De term van de hoogste graad in de uitbreiding van (3x – 2y) 6 wordt gevonden in de combinatie (3x) p (-2y) (6-p) , waarbij p de waarde is die de exponent van (3x) p maakt en (-2y) (6-p) gelijk aan de graad van de binominale waarde, namelijk 6.
Daarom is de term van de hoogste graad:
(3x) 3 (-2y) 3 = -216x 3 en 3