Coplanaire (of coplanaire) punten

Op deze pagina ontdekt u wat coplanaire (of coplanaire) punten zijn en hoe u kunt weten of bepaalde punten coplanair zijn of niet. Daarnaast kunt u voorbeelden zien en oefenen met opgeloste coplanaire puntoefeningen.

Wat zijn coplanaire punten?

In de analytische meetkunde is de betekenis van coplanaire (of coplanaire) punten als volgt:

Coplanaire punten zijn punten die tot hetzelfde vlak behoren.

Daarom zijn 2 of 3 punten altijd coplanair, omdat een vlak kan worden gevormd met slechts 3 punten. Aan de andere kant, als er 4, 5 of meer punten zijn, is het mogelijk dat sommige punten niet in hetzelfde vlak liggen en daarom niet coplanair zijn.

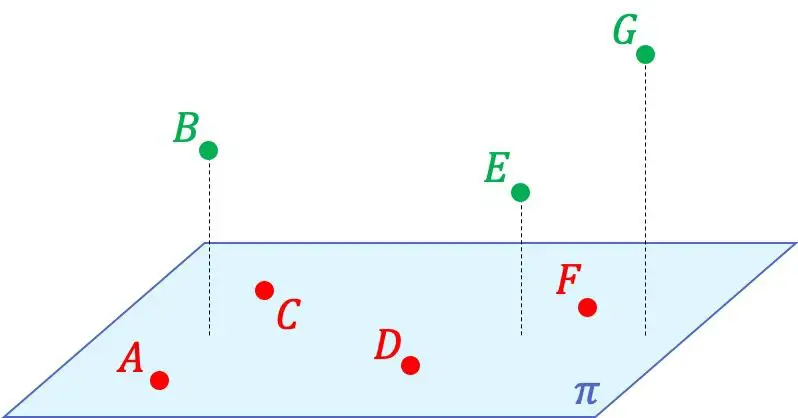
In de grafische weergave hierboven kunt u bijvoorbeeld zien dat de punten A, C, D en F in hetzelfde vlak liggen, omdat ze zich in hetzelfde vlak bevinden. Aan de andere kant liggen deze 4 punten niet in hetzelfde vlak als de punten B, E en G, omdat er geen vlak kan worden gevormd in de ruimte die alle punten bevat.

Uit deze eigenschap kunnen we afleiden dat de vectoren die worden gedefinieerd door coplanaire punten ook coplanaire vectoren zijn, dat wil zeggen dat ze zich in hetzelfde vlak bevinden.

Wanneer zijn punten coplanair?

Zoals we hebben gezien bij de definitie van coplanaire (of coplanaire) punten, zijn twee of drie punten altijd coplanair, maar meer dan drie punten hoeven de coplanariteitsrelatie niet te respecteren.

Er zijn dus hoofdzakelijk twee methoden om te bepalen of vier of meer punten coplanair zijn:

Eén manier om te weten of de punten coplanair zijn, is door de vectoren te gebruiken die door de punten worden bepaald: als deze vectoren coplanair zijn , dan zijn de punten ook coplanair.

Om deze methode toe te passen, moet je uiteraard weten wanneer de vectoren coplanair zijn. Maar aangezien er ook verschillende manieren zijn om te bepalen of een set vectoren coplanair is, raden we aan om te kijken hoe je kunt bepalen of vectoren coplanair zijn . Hier vindt u alle procedures die bestaan om te bepalen wanneer 2, 3, 4 of meer vectoren coplanair zijn, evenals voorbeelden en opgeloste oefeningen.

Een andere manier om te weten of een reeks punten coplanair is, is door de vergelijking te vinden van het vlak dat wordt gevormd door 3 punten in de set, en als de andere punten aan deze vergelijking voldoen, betekent dit dat alle punten in de set coplanair zijn.

Hoewel het afhankelijk is van het probleem, raden we aan de eerste van de twee methoden te gebruiken, omdat het veel eenvoudiger en sneller is om te controleren of de vectoren coplanair zijn dan om de vergelijking van een vlak te berekenen. Maar gebruik uiteraard wat u verkiest.

Coplanaire puntproblemen opgelost

Oefening 1

Bepaal of de volgende drie punten coplanair zijn:

$A(3,5,1)$

$B(0,-2,3)$

$C(4,-1,2)$

zie oplossing

In dit geval is het niet nodig om berekeningen uit te voeren, omdat 3 punten altijd coplanair zijn , wat ze ook mogen zijn.

Oefening 2

Bepaal of de volgende vier punten coplanair zijn:

$A(1,2,0)$

$B(-1,3,4)$

$C(1,0,-1)$

$D(2,5,-3)$

zie oplossing

Om de vier punten coplanair te laten zijn, moeten de daardoor bepaalde vectoren coplanair zijn. We berekenen daarom deze vectoren:

$\vv{AB} = B- A = (-1,3,4)-(1,2,0) = (-2,1,4)$

$\vv{AC} = C- A = (1,0,-1)-(1,2,0) = (0,-2,-1)$

$\vv{AD} = D- A = (2,5,-3)-(1,2,0) = (1,3,-3)$

Laten we nu de matrix construeren die wordt gevormd door de vectoren:

$\displaystyle A= \begin{pmatrix} -2&1&4 \\[1.1ex]0&-2&-1 \\[1.1ex] 1&3&-3\end{pmatrix}$

Om de resulterende vectoren coplanair te laten zijn, moet de rangorde van de vorige matrix gelijk zijn aan 2. En hiervoor moet de determinant van de gehele 3×3-matrix gelijk zijn aan nul:

$rg(A)= \ ?$

$\displaystyle \begin{vmatrix} -2&1&4 \\[1.1ex]0&-2&-1 \\[1.1ex] 1&3&-3\end{vmatrix} =-11\neq 0$

$rg(A)=3$

De determinant van de gehele matrix is echter niet nul, dus de rangorde van de matrix is 3, en daarom zijn de 4 punten niet coplanair .

Oefening 3

Ontdek of de volgende vijf punten coplanair zijn:

$A(3,1,1)$

$B(0,0,2)$

$C(4,-2,-1)$

$D(-1,1,3)$

$E(2,4,3)$

zie oplossing

Om alle vijf punten coplanair te laten zijn, moeten de vectoren die erdoor worden gedefinieerd coplanair zijn. We berekenen daarom deze vectoren:

$\vv{AB} = B- A = (0,0,2)-(3,1,1) = (-3,-1,1)$

$\vv{AC} = C- A = (4,-2,-1)-(3,1,1) = (1,-3,-2)$

$\vv{AD} = D- A = (-1,1,3)-(3,1,1) = (-4,0,2)$

$\vv{AE} = E- A = (2,4,3)-(3,1,1) = (-1,3,2)$

Laten we nu de matrix construeren die uit de vectoren bestaat:

$\displaystyle A= \begin{pmatrix} -3&-1&1 \\[1.1ex]1&-3&-2 \\[1.1ex] -4&0&2\\[1.1ex] -1&3&2\end{pmatrix}$

Om de resulterende vectoren coplanair te laten zijn, moet de rangorde van de vorige matrix gelijk zijn aan 2. We berekenen daarom de rangorde van de matrix van vectoren op basis van determinanten om te controleren of ze coplanair zijn:

$rg(A)= \ ?$

$\displaystyle \begin{vmatrix} -3&-1&1 \\[1.1ex]1&-3&-2 \\[1.1ex] -4&0&2\end{vmatrix} = 0 \qquad \begin{vmatrix} -3&-1&1 \\[1.1ex]1&-3&-2 \\[1.1ex] -1&3&2\end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} -3&-1&1 \\[1.1ex] -4&0&2\\[1.1ex] -1&3&2\end{vmatrix} = 0 \qquad \begin{vmatrix} 1&-3&-2 \\[1.1ex] -4&0&2\\[1.1ex] -1&3&2\end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} -3&-1 \\[1.1ex] 1&-3\end{vmatrix} =10\neq 0$

$rg(A)=2$

De rangorde van de matrix is gelijk aan 2, dus de vectoren zijn coplanair en daarom zijn de 5 punten ook coplanair.

Oefening 4

Bereken parameterwaarde

$k$

zodat de volgende 4 punten coplanair zijn:

$A(3,1,4)$

$B(2,1,2)$

$C(0,-1,3)$

$D(3,2,k)$

zie oplossing

Om de vier punten coplanair te laten zijn, moeten de daardoor bepaalde vectoren coplanair zijn. We berekenen daarom deze vectoren:

$\vv{AB} = B- A = (2,1,2)-(3,1,4) = (-1,0,-2)$

$\vv{AC} = C- A = (0,-1,3)-(3,1,4) = (-3,-2,-1)$

$\vv{AD} = D- A = (3,2,k)-(3,1,4) = (0,1,k-4)$

Wiens vectormatrix is:

$\displaystyle A= \begin{pmatrix} -1&0&-2 \\[1.1ex] -3&-2&-1 \\[1.1ex] 0&1&k-4\end{pmatrix}$

Om de resulterende vectoren coplanair te laten zijn, moet de rangorde van de matrix 2 zijn. En daarom moet de determinant van de gehele 3×3-matrix 0 zijn:

$\displaystyle \begin{vmatrix} -1&0&-2 \\[1.1ex] -3&-2&-1 \\[1.1ex] 0&1&k-4\end{vmatrix} =0$

$\displaystyle 2k-3 =0$

Eindelijk lossen we het onbekende op

$k:$

$2k =3$

$\bm{k =}\mathbf{\cfrac{3}{2}}$

Ten slotte, als dit artikel nuttig voor u was, bent u waarschijnlijk ook geïnteresseerd in hoe de afstand tussen twee punten wordt berekend (formule) , aangezien ons bij analytische meetkundeproblemen soms wordt gevraagd wat de afstand tussen twee punten is. Op de gelinkte pagina vindt u een zeer gedetailleerde uitleg, evenals voorbeelden en oefeningen die stap voor stap worden opgelost.

Wat zijn coplanaire punten?

Wanneer zijn punten coplanair?

Coplanaire puntproblemen opgelost

Oefening 1

Oefening 2

Oefening 3

Oefening 4

Laat een reactie achter Reactie annuleren