▷ Hoe weet je of een functie continu is (opgeloste oefeningen)

In dit artikel leggen we uit wat continue functies zijn en hoe je kunt bepalen of een functie op een bepaald punt continu is of niet. Daarnaast vindt u eigenschappen van continue functies en continuïteitsanalyses van de meest voorkomende functies. Ten slotte kun je oefenen met opgeloste oefeningen over de continue functie om het concept volledig te begrijpen.

Wat is een continue functie?

De continuïteit van een functie kan grafisch worden bestudeerd. Een continue functie is een functie die in een grafiek kan worden weergegeven zonder het potlood van het papier te halen.

Continue functie

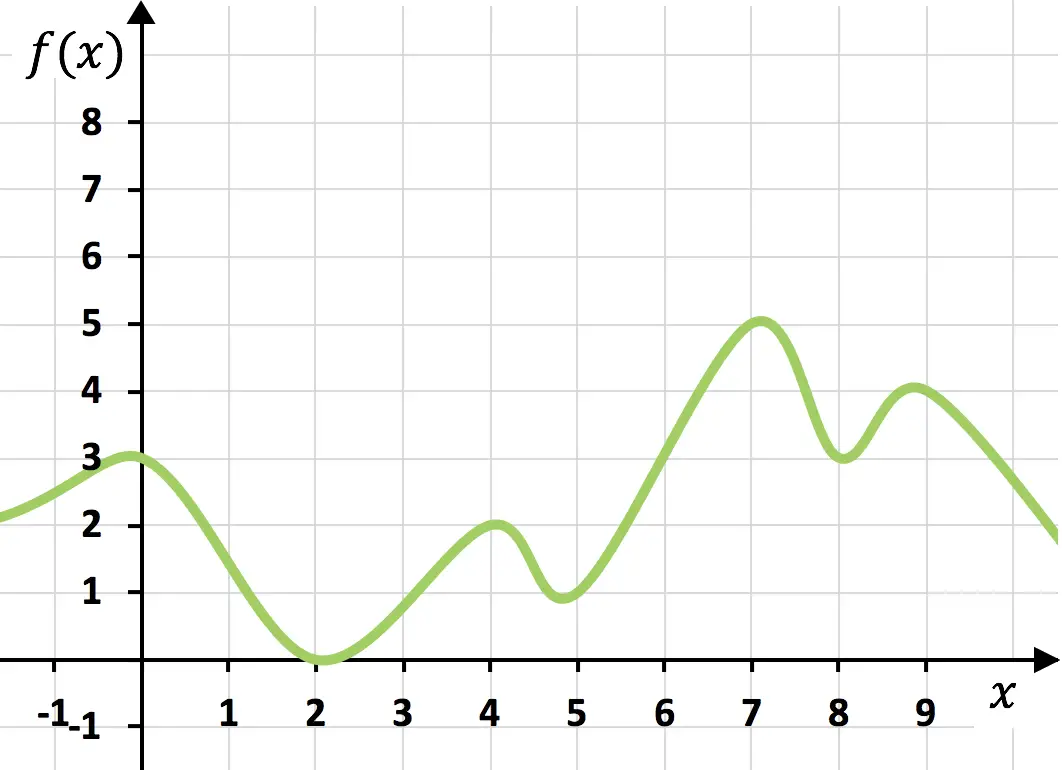
De bovenstaande functie is continu omdat deze in één beweging kan worden getekend zonder uw hand van het papier te halen.

Aan de andere kant, wanneer de vorige continuïteitsvoorwaarde niet in een functie wordt geplaatst, wordt er gesproken van een discontinue functie .

Discontinue functie

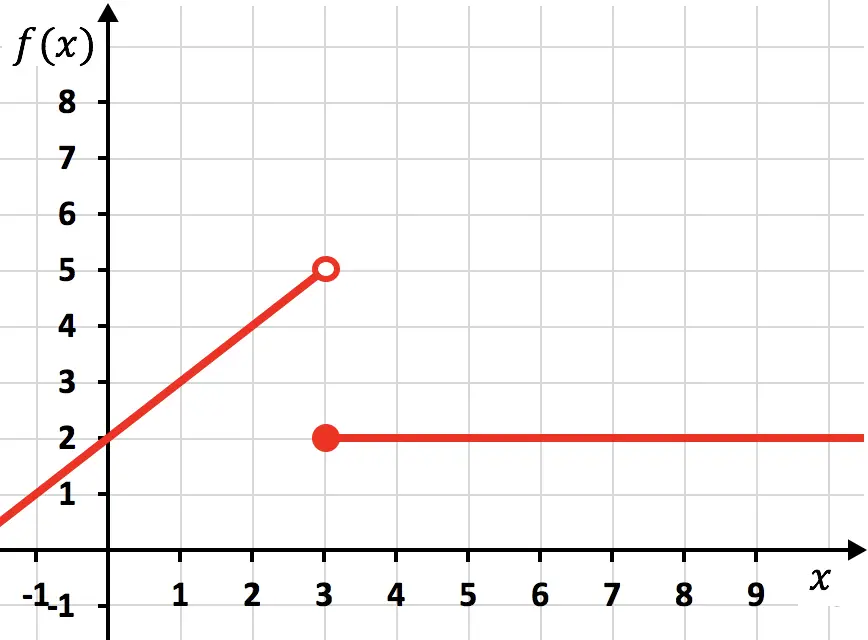
De vorige functie is discontinu omdat je om deze weer te geven twee lijnen moet maken met het potlood. In dit geval houdt de functie op continu te zijn bij x=3, daarom zeggen we dat x=3 een punt van discontinuïteit is.

Bovendien zijn er drie soorten discontinuïteiten : vermijdbare discontinuïteit, onvermijdelijke discontinuïteit met eindige sprongen en onvermijdelijke discontinuïteit met oneindige sprongen. In de volgende link kunt u zien hoe elk type discontinuïteit eruit ziet en wat er aan elk type verschillend is:

➤ Zie: soorten discontinuïteiten

Continuïteit van een functie op een punt

Zodra we zien hoe de grafiek van een continue functie eruit ziet, zullen we kijken hoe we analytisch kunnen bepalen of een functie continu is of niet.

Wiskundig gezien is een functie continu op een punt als aan de volgende drie voorwaarden is voldaan:

De functie bestaat op dit punt, dat wil zeggen dat het beeld van het punt bestaat.

$\exists \ f(a)$

Er is op dit punt de grens van de functionaliteit. Daarom zijn de linker en rechter laterale grenzen van de functie op dit punt gelijk.

$\displaystyle \lim_{x \to a^-} f(x) = \lim_{x \to a^+} f(x) \quad \color{orange}\bm{\longrightarrow}\color{black} \quad \exists \lim_{x \to a} f(x)$

Het beeld van het punt valt op dit punt samen met de limiet van de functie.

$\displaystyle f(a)=\lim_{x \to a} f(x)$

Als dus op alle punten van een functie aan de drie continuïteitsvoorwaarden wordt voldaan, is de functie continu.

Als voorbeeld analyseren we de continuïteit van de volgende stuksgewijze functie:

continuïteit van een stuksgewijs gedefinieerde functie

Zelfs als je op dat moment van sectie verandert

$x=-2$

De functie is continu, aangezien de laterale grenzen van de functie op dit punt gelijk zijn en meer samenvallen met de waarde van de functie op dit punt.

$\lim\limits_{x \to -2^-} f(x)=\lim\limits_{x \to -2^+} f(x)= f(-2)=3$

Aan de andere kant is de functie op dit punt niet continu

$x=4$

omdat de twee laterale limieten verschillend zijn en daarom de limiet van de functie op dit punt niet bestaat:

$\lim\limits_{x \to 4^-} f(x)=3 \neq \lim\limits_{x \to 4^+} f(x)= 2$

Kortom, de functie gedefinieerd door de stukken is continu in alle reële getallen behalve in

$x=4,$

waar sprake is van discontinuïteit.

We kunnen ook verifiëren dat de functie discontinu is in

$x=4$

omdat het voor een grafische weergave noodzakelijk is om het potlood op dit punt van het papier te verwijderen.

Continuïteit van elementaire functies

Bepaalde soorten functies zijn continu door hun kenmerken:

Constante functies zijn continu in alle reële getallen.

$f(x)=k$

Polynoomfuncties zijn continu voor alle reële getallen.

$f(x)=a_0+a_1x+a_2x^2+a_3x^3+\dots+a_nx^n$

Rationele (of fractionele) functies zijn continu in alle reële getallen, behalve in waarden die de noemer van de breuk opheffen; op deze punten vertoont de functie een discontinuïteit.

$f(x)=\cfrac{p(x)}{q(x)}$

Exponentiële functies zijn continu over alle reële getallen:

$f(x)=a^x$

Logaritmische functies zijn continu op alle punten die hun argument positief maken.

$f(x)=\log_a (x)$

De continuïteit van irrationele functies , of functies met wortels, hangt af van de index van de radicaal (n). Als de index even is, zijn dit continue functies op alle punten die het wortelargument gelijk aan of groter dan nul maken. Maar als de index oneven is, zijn het continue functies voor alle reële getallen.

$f(x)=\sqrt[n]{x}$

De continuïteit van goniometrische functies hangt af van het type functie. De sinusfunctie en de cosinusfunctie zijn continu over de reeks reële getallen, maar de raaklijnfunctie is discontinu op de punten
$\displaystyle x=\frac{\pi}{2}+k\pi$

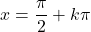
(waarbij k een geheel getal is).

$f(x)=sen(x)\qquad f(x)=cos(x)\qquad f(x)=tg(x)$

Eigenschappen van continue functies

Sean

$f(x)$

$g(x)$

twee continue functies op het punt

$x=a,$

De som van twee continue functies op een punt is op dat punt een andere continue functie.

$f(x)+g(x)$

Het product van twee continue functies op een punt is gelijk aan een andere continue functie op dat punt.

$f(x)\cdot g(x)$

Het delen van twee continue functies op een bepaald punt resulteert in een andere continue functie op dat punt, zolang dat punt de deelfunctie niet opheft.

$\cfrac{f(x)}{g(x)}\qquad g(a)\neq 0$

De samenstelling van twee continue functies op een punt geeft aanleiding tot een continue functie op hetzelfde punt.

$f(x)\circ g(x)$

➤ Zie: wat is een samengestelde functie?

Opgeloste oefeningen over de continuïteit van een functie

Oefening 1

Zoek de discontinuïteiten van de functie die in de volgende grafiek wordt weergegeven. Bepaal ook om welk type discontinuïteit het gaat.

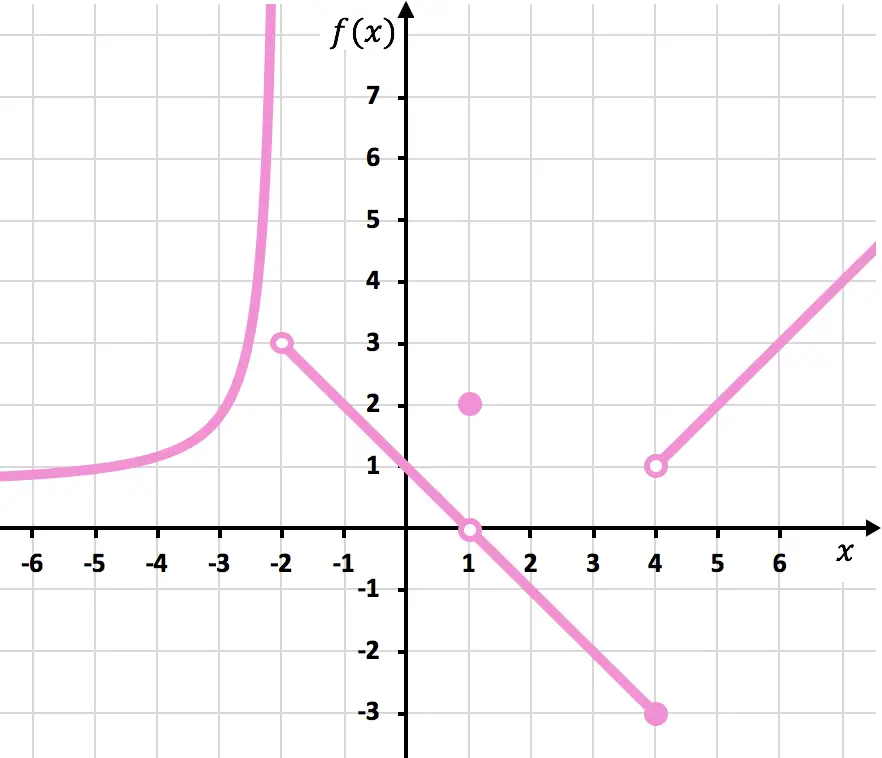
oefening loste de discontinuïteiten van functies op

Let op: om deze oefening uit te voeren raden wij u aan eerst te kijken wat de verschillende soorten discontinuïteiten zijn en hoe ze worden geïdentificeerd. U kunt de uitleg zien in de link over het principe van discontinuïteittypen .

Zie de oplossing

Om de functie te tekenen moet u het potlood omhoog brengen bij x=-2, bij x=1 en bij x=4. De functie is dus discontinu op deze drie punten.

Bij x=-2 is de linkergrens +∞ en de rechtergrens 3. Aangezien een van de zijgrenzen oneindig is, heeft de functie dus een onvermijdelijke oneindige sprongdiscontinuïteit bij x=-2.

$\displaystyle \lim_{x \to -2^-} f(x) = +\infty \ \neq \ \lim_{x \to -2^+} f(x) = 3$

De limiet van de functie bij x=1 is 0 en aan de andere kant is de waarde van de functie bij x=1 gelijk aan 2. De functie vertoont daarom een vermijdbare discontinuïteit bij x=1.

$\displaystyle \lim_{x \to 1^-} f(x) = \lim_{x \to 1^+} f(x) = 0 \ \bm{\longrightarrow} \ \lim_{x \to 1} f(x) = 0$

$\displaystyle \lim_{x \to 1} f(x) = 0 \neq f(0) = 2$

Bij x = 4 is de linkergrens -3 en de rechtergrens 1. Aangezien de twee zijgrenzen verschillend zijn en geen van beide oneindig geeft, heeft de functie onvermijdelijk een eindige sprongdiscontinuïteit bij x = 4.

$\displaystyle \lim_{x \to 4^-} f(x) = -3 \ \neq \ \lim_{x \to 4^+} f(x) = 1$

Oefening 2

Bepaal de punten waarop de functie in de volgende grafiek discontinu is.

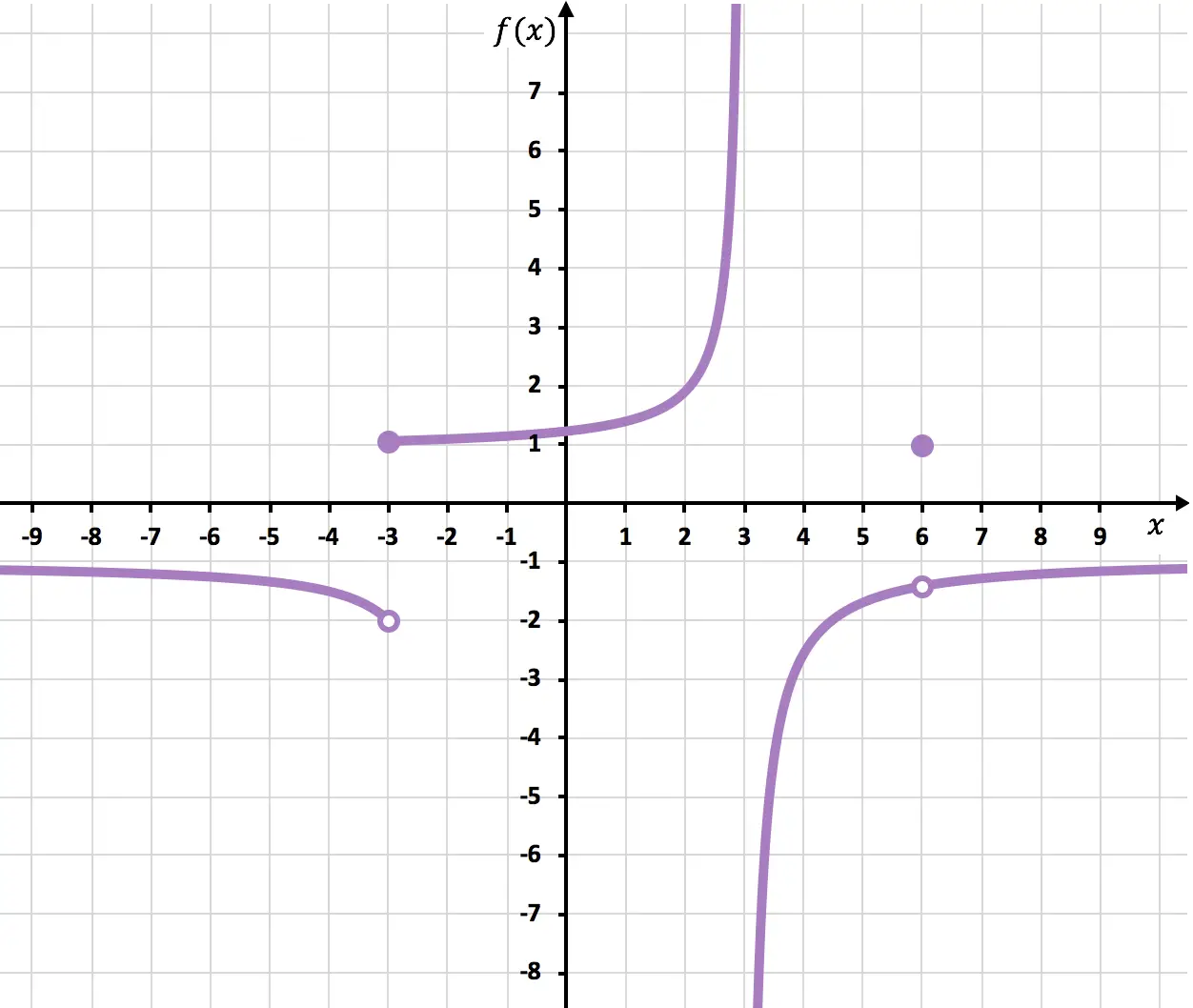
opgeloste oefening over de soorten discontinuïteiten van een functie

Zie de oplossing

Op punt x=6 wordt de functie onderbroken omdat er een open punt is. De limiet als x 6 nadert is -1,4 maar f(6)=1. De functie heeft daarom een vermijdbare discontinuïteit bij x=6 omdat de waarde van de limiet niet samenvalt met de waarde van de functie:

$\displaystyle \left. \begin{array}{l} \displaystyle \lim_{x \to 6^-} f(x)=-1,4\\[3ex] \displaystyle \lim_{x \to 6^+} f(x)=-1,4 \end{array} \right\} \bm{\longrightarrow} \lim_{x \to 6} f(x)=-1,4$

$\displaystyle\lim_{x \to 6} f(x)=-1,4 \neq f(6)=1$

Bij x=-3 vallen de laterale grenzen niet samen en geen enkele geeft oneindigheid. De functie heeft daarom een onvermijdelijke eindige sprongdiscontinuïteit bij x=-3.

$\displaystyle \lim_{x \to -3^-} f(x)=-2 \neq \lim_{x \to -3^+} f(x)=1$

En ten slotte heeft de functie een onvermijdelijke oneindige sprongdiscontinuïteit bij x = 3, aangezien ten minste één laterale limiet op dit punt resulteert in oneindigheid.

$\displaystyle \lim_{x \to 3^-} f(x)=+\infty \qquad \lim_{x \to 3^+} f(x)=-\infty$

Oefening 3

Analyseer de continuïteit van de volgende rationale functie:

$\displaystyle f(x)= \frac{2}{x-5}$

Zie de oplossing

Rationele functies zijn continu in hun hele domein, dat wil zeggen in alle reële getallen behalve de waarden die de noemer opheffen. Daarom stellen we de noemer van de rationale functie gelijk aan nul om te zien welke punten niet tot het domein behoren:

$x-5=0$

$x=5$

$\text{Dom } f = \mathbb{R} - \{5\}$

De functie zal daarom op alle punten continu zijn, behalve x=5.

Oefening 4

Analyseer de continuïteit van de volgende stuksgewijze functie:

$\displaystyle f(x)= \left\{ \begin{array}{lcl} 5x-2 & \text{si} & x < 1 \\[2ex] x^2+2 & \text{si} & x \geq 1 \end{array} \right.$

Zie de oplossing

De functie is ook continu in het eerste deel,

$5x-2$

, zoals in het tweede deel,

$x^2+2$

, omdat het polynomiale functies zijn.

Het enige punt waarop de functie discontinu zou kunnen zijn, is dus het punt waar de functie stuksgewijs breekt. Laten we dus de laterale grenzen op dit punt berekenen:

$\displaystyle \lim_{x \to 1^-} f(x) = \lim_{x \to 1} (5x-2)=5\cdot 1-2=\bm{3}$

$\displaystyle \lim_{x \to 1^+} f(x) = \lim_{x \to 1} (x^2+2)=1^2+2=\bm{3}$

De twee laterale grenzen vallen dus samen, de limiet van de functie wanneer x naar 1 neigt, is gelijk aan 3:

$\displaystyle \lim_{x \to 1^-} f(x) = \lim_{x \to 1^+} f(x) = 3 \ \bm{\longrightarrow} \ \exists \lim_{x \to 1} f(x) = 3$

Bovendien is het beeld van x=1 ook 3:

$f(1)=1^2+2=\bm{3}$

Aangezien de limiet van de functie op x=1 gelijk is aan het beeld van genoemd punt, is de functie dus continu op punt x=1. En daarom is het continu in alle reële getallen.

$\displaystyle f(1)=\lim_{x \to 1} f(x)$

Oefening 5

Bestudeer de continuïteit van de volgende irrationele functie:

$f(x)=\sqrt{2x+6}$

Zie de oplossing

Het is een radicaalfunctie met een even index, dus de functie zal continu zijn zolang het argument van het radicaal groter is dan 0 (omdat de vierkantswortel van een negatief getal niet bestaat):

$2x+6\ge 0$

We lossen de ongelijkheid op:

$2x\ge -6$

$x\ge \cfrac{-6}{2}$

$x\ge -3$

De oplossing bestaat uit alle getallen groter dan of gelijk aan -3. De functie is daarom continu op het interval van zijn domein:

$\mathbf{Dom } \ \bm{f = [-3,+\infty) }$

Oefening 6

Analyseer de continuïteit van de volgende logaritmische functie:

$f(x)=\log_3 (-3x+6)$

Zie de oplossing

Dit is een logaritmische functie en er is noch de logaritme van een negatief getal, noch de logaritme van 0. Daarom zal de functie bestaan zolang het argument van de logaritme positief is (groter dan nul):

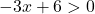$-3x+6>0″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”95″ style=”vertical-align: -2px;”> <p class=$ We lossen de ongelijkheid op:

$-3x>-6″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”78″ style=”vertical-align: -2px;”> <p class=$ $x<\cfrac{-6}{-3}$

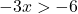
Onthoud dat wanneer je een negatief getal deelt door de andere kant van een ongelijkheid, je het teken van de ongelijkheid moet omkeren.

$x<2$

De oplossing bestaat uit alle getallen kleiner dan 2. Het definitiedomein van de functie is daarom:

$\mathbf{Dom } \ \bm{f = (-\infty,2) }$

De functie is daarom continu op elk punt in zijn domein.

Oefening 7

Bereken de continuïteit van de volgende functie:

$f(x)=\cfrac{4x-2}{\sqrt{-2x-8}}$

Zie de oplossing

In de noemer van de breuk hebben we een radicaal met een even index, dus de functie zal bestaan wanneer de inhoud van de wortel gelijk is aan of groter is dan nul:

$-2x-8\geq 0$

Maar de wortel ligt ook in de noemer van de breuk, en de noemer van een breuk kan nooit 0 zijn. De functie zal dus alleen bestaan als de inhoud van de wortel strikt groter is dan 0:

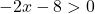$-2x-8> 0″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”95″ style=”vertical-align: -2px;”> <p class=$ Nu lossen we de ongelijkheid op:

$-2x>8″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”64″ style=”vertical-align: -2px;”> <p class=$ $x<\cfrac{8}{-2}$

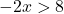
Bedenk dat wanneer we de zijden van een negatief getal veranderen door een ongelijkheid te vermenigvuldigen of te delen, we ook het ongelijkheidsteken moeten roteren.

$x<-4$

Het resultaat is alle getallen kleiner dan -4. Het domein van de functie, en dus de continuïteit ervan, wordt dus gedefinieerd door het volgende interval:

$\mathbf{Dom } \ \bm{f = (-\infty,-4) }$

Oefening 8

Bereken de waarde van k zodat de functie overal continu is

$\mathbb{R} .$

$\displaystyle f(x)= \left\{ \begin{array}{lcl} kx-1 & \text{si} & x \leq 2 \\[2ex] 3x^2 - 5 & \text{si} & x > 2 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”65″ width=”225″ style=”vertical-align: 0px;”> <div class=$

Zie de oplossing

Om de functie continu te laten zijn, moeten de twee laterale limieten op het breekpunt hetzelfde resultaat opleveren. We berekenen daarom eerst de laterale grens op het breekpunt van het onderdeel dat geen k heeft:

$\displaystyle \lim_{x \to 2^+} f(x) = \lim_{x \to 2} (3x^2 - 5) = 3\cdot 2^2-5=\bm{7}$

Om de stuksgewijze functie continu te laten zijn, moet de limiet van de andere zijde daarom ook gelijk zijn aan 7.

$\displaystyle \lim_{x \to 2^-} f(x) = \lim_{x \to 2} (kx-1) = k\cdot2 -1= 2k-1$

Om de functie continu te laten zijn, moeten de twee laterale grenzen van elk punt dus hetzelfde resultaat opleveren. We stellen daarom de uitdrukking verkregen uit de limiet gelijk aan 7 (het resultaat van de andere laterale limiet).