Constante functie - Mathority

In dit artikel leggen we uit wat een constante functie is en wat de grafische weergave ervan is. Bovendien kunt u verschillende voorbeelden van constante functies en alle kenmerken van dit type functie zien. En ten slotte kun je trainen met opgeloste oefeningen van constante functies.

Wat is een constante functie?

Een constante functie is die functie die altijd hetzelfde beeld aanneemt voor elke waarde van de onafhankelijke variabele (x) , dwz een constante functie heeft de vorm f(x)=k , waarbij k een willekeurig reëel getal is.

$f(x)=k$

De grafische weergave van een constante functie is een horizontale lijn.

Alle volgende functies zijn bijvoorbeeld constanten:

$f(x)=1 \qquad f(x)=7 \qquad f(x)=5$

Grafische weergave van een constante functie

Zodra we het concept van een constante functie hebben gezien, zullen we zien hoe we een constante functie in een grafiek kunnen weergeven.

Het tekenen van een constante functie is vrij eenvoudig: teken gewoon een horizontale lijn in de waarde van de functie (k).

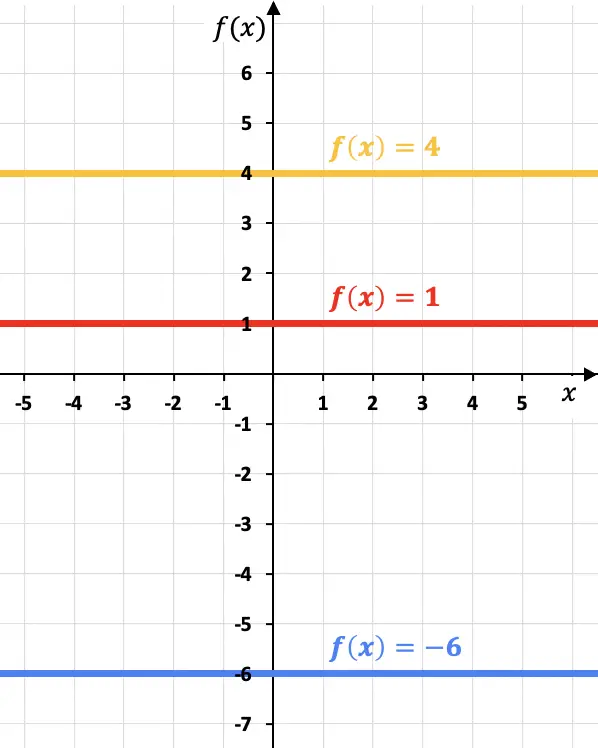
Bekijk de volgende voorbeelden waarin we drie verschillende constante functies in een grafiek hebben weergegeven:

Merk op dat elke constante functie evenwijdig is aan de x-as.

Aan de andere kant moet je er rekening mee houden dat een verticale lijn geen constante functie is. In feite is een verticale lijn niet eens een functie, aangezien een functie per definitie slechts één afbeelding kan hebben voor elke waarde van x.

Kenmerken van de constante functie

Vervolgens zullen we de eigenschappen van de constante functie analyseren. Beschouw een constante functie van elke waarde:

$f(x)=k$

Het domein van de constante functie bestaat uit alle reële getallen:

$\text{Dom } f = \mathbb{R}$

Het pad of bereik van de constante functie is alleen de waarde van de constante:

$\text{Im } f= k$

Het is een continue en even functie, omdat de functie altijd dezelfde waarde heeft:

$\displaystyle f(x)=f(-x)$

De constante functie neemt niet toe of af, het is een type functie dat altijd een nulhelling heeft:

$m=0$

Het snijdt altijd de OY-as in het punt (0,k).

$(0,k)$

Elke constante functie is een polynoom van graad nul.

Ja
$k\neq 0$

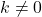
de constante functie heeft geen wortel, in plaats daarvan if

$k=0$

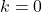
alle reële getallen zijn de wortels van de constante functie.

De limiet van de constante functie naarmate x plus oneindig of min oneindig nadert, is gelijk aan de waarde van de constante:

$\displaystyle\lim_{x\to +\infty} f(x)=k$

$\displaystyle\lim_{x\to -\infty} f(x)=k$

De afgeleide van de constante functie is altijd nul:

$f(x)=k \ \longrightarrow \ f'(x)=0$

In feite kan de definitie van de constante functie ook worden gedaan vanuit het begrip afgeleide: een functie is constant als zijn afgeleide over zijn hele domein verdwijnt.

De integraal van de constante functie is de lineaire (of affiene) functie:

$\displaystyle \int k \ dx= x + C$

➤ Zie: Wat is een lineaire functie?

Constante functie op een interval

We hebben gezien hoe een functie constant is, maar een functie kan alleen constant zijn in een interval van zijn domein.

Om dit concept te begrijpen, moet je weten welke functies in stukjes zijn gedefinieerd. Voordat we verder gaan, raden we je aan de volgende uitleg te bekijken:

➤ Zie: Wat is een stuksgewijze functie?

Als je eenmaal weet wat dit soort functies zijn, kijk dan naar de functie die is gedefinieerd in de onderstaande onderdelen:

Zoals je in de grafiek kunt zien, is de functie niet constant voor alle getallen in zijn domein. Maar het is constant in het interval [-2,4), dus het is slechts een constante functie in één interval.