Op deze pagina vindt u de definitie van kegelsneden, waarom ze zo belangrijk zijn en de verschillende soorten kegelsneden die er bestaan (cirkel, ellips, hyperbool en parabool). Bovendien kunt u de verschillen tussen hun vergelijkingen zien.
Wat zijn kegelsneden?
In de analytische meetkunde zijn kegelsneden (of eenvoudigweg kegelsneden) alle krommen die het resultaat zijn van de verschillende snijpunten tussen een kegel en een vlak, wanneer dit vlak niet door de top van de kegel gaat. Er zijn vier soorten kegelsneden: de cirkel, de ellips, de parabool en de hyperbool.
Hieronder staan de 4 mogelijke secties die uit elke kegel kunnen worden verkregen:
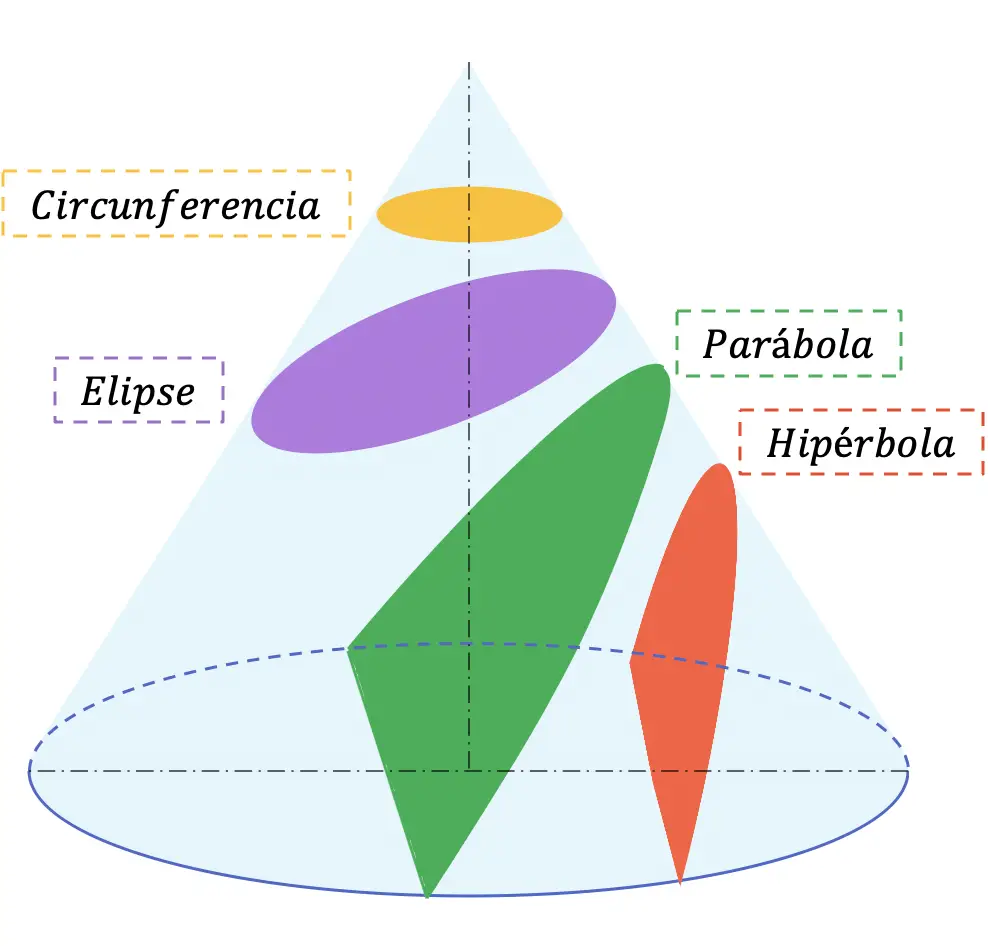
Kegelsneden worden over het algemeen bestudeerd op de middelbare school (Bachillerato), in de vakken wiskunde en technisch tekenen.
Soorten kegelsneden
Als we eenmaal het concept kegelsnede hebben gezien, gaan we kijken welke vier soorten kegelsneden er bestaan: de cirkel, de ellips, de parabool en de hyperbool.
omtrek
De omtrek is een kegelvormig gedeelte dat kan worden gevonden door een kegel af te snijden met een vlak loodrecht op de omwentelingsas (parallel aan de basis).

Bovendien is de omtrek de verzameling punten op het vlak die op gelijke afstand liggen van een vast punt dat het middelpunt wordt genoemd.
Ovaal
De ellips is een platte, gesloten, gebogen lijn die sterk lijkt op de omtrek, maar de vorm is meer ovaal. In het bijzonder is dit het gevolg van het snijden van het oppervlak van een kegel door een schuin vlak waarvan de hoek ten opzichte van de omwentelingsas groter is dan die van de generator.
Bovendien voldoen alle punten van een ellips aan een voorwaarde: de ellips is de meetkundige plaats van alle punten van een vlak waarvan de som van de afstanden tot twee andere vaste punten (de zogenaamde brandpunten F en F’) constant is.

Gelijkenis
In de wiskunde is een parabool de verzameling punten op het vlak die op gelijke afstand liggen van een vast punt (het brandpunt genoemd) en een vaste lijn (de richtlijn genoemd).

Geometrisch gezien is de parabool het resultaat van de doorsnede van een kegel door een vlak met een hellingshoek ten opzichte van de omwentelingsas die gelijk is aan de hoek van de beschrijvende lijn van de kegel. Daarom is het vlak dat de parabool bevat evenwijdig aan de generator van de kegel.
Een heel belangrijk kenmerk van deze kegelsnede is de paraboolvergelijking , omdat we, afhankelijk van de toestand ervan, kunnen identificeren welk type parabool het is. In deze link vind je alle vergelijkingen van de parabool, wat de elementen van de parabool zijn, hun eigenschappen, voorbeelden, opgeloste oefeningen,… naast andere kenmerken van parabolen.
Hyperbool
Als kegelsnede wordt een hyperbool verkregen wanneer een kegel wordt gesneden door een vlak met een hoek kleiner dan de hoek gevormd door de generator van de kegel ten opzichte van zijn omwentelingsas.
Wiskundig gezien kan een hyperbool worden gedefinieerd als de verzameling punten op het vlak die aan de volgende eigenschap voldoen: de absolute waarde van het verschil in afstanden tussen elk punt op de hyperbool en twee vaste punten (de zogenaamde brandpunten) moet constant zijn.
Bovendien is de waarde van het aftrekken van deze twee afstanden altijd gelijk aan de afstand tussen de twee hoekpunten van de hyperbool.
![]()

Zoals je vast al hebt afgeleid, de parameterwaarde
![]()
van een hyperbool is van fundamenteel belang voor hyperbolen. In de volgende link kunt u onze uitleg van de hyperbool zien, waar u zult ontdekken waarom het zo’n belangrijke coëfficiënt is en wat alle elementen zijn die een hyperbool karakteriseren. Bovendien ontdek je hoe de vergelijking van een hyperbool eruit ziet, welke verschillende soorten hyperbolen er bestaan, en zelfs stapsgewijze problemen en oefeningen met hyperbolen.
Algemene vergelijking van kegelsneden
Elke kegelsnede kan analytisch worden uitgedrukt als een vergelijking. In feite moeten alle kegelsnedevergelijkingen van de tweede graad zijn:
![]()
Bijgevolg ten minste één van de coëfficiënten
![]()
of
![]()
van de formule mag niet nul zijn.
Afhankelijk van de parameterwaarden komt de vergelijking dus overeen met het ene of het andere type kegelsnede:
- Omtrek : voor de algemene vergelijking die een omtrek beschrijft, de termen

En

moet overeenkomen met en

moet nul zijn.
![]()
- Ellips : De vergelijking komt overeen met de wiskundige uitdrukking van een ellips wanneer de volgende voorwaarde is geverifieerd:
![]()
- Parabool : Om de vergelijking een parabool te laten zijn, moet aan de volgende gelijkheid worden voldaan:
![]()
- Hyperbool : Ten slotte moet de algemene vergelijking van een hyperbool aan de volgende ongelijkheid voldoen:
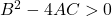 Bericht navigatie
Bericht navigatie