Je hebt waarschijnlijk wel eens gehoord van complexe getallen . Ze zijn misschien wel de moeilijkste reeks getallen om mee om te gaan, omdat ze echte en denkbeeldige getallen combineren. De unificatie ervan maakt het mogelijk om numeriek gedrag te bestuderen dat niet met alle reële getallen kan worden behandeld.
Wat zijn complexe getallen?
Complexe getallen zijn de combinatie van een reëel getal en eendenkbeeldig getal . 4 + 5i is bijvoorbeeld een complex getal met een reëel deel gelijk aan 4 en een imaginair deel gelijk aan 5i. Over het algemeen kunnen we ze uitdrukken met de volgende formule:
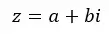
Waarbij Re(z) = a en Im(z) = b
Zoals we al zeiden, zijn complexen de grootste verzameling of globale verzameling , die zowel reële getallen als denkbeeldige getallen omvat. Vervolgens laten we u een klein diagram zien van de hiërarchische structuur van alle sets:

Als we dus een combinatie hebben van een reëel getal en een denkbeeldig getal, hebben we een complex getal. Maar er zijn momenten waarop een van de twee delen gelijk is aan nul. Wat gebeurt er in deze gevallen? Welnu, we hebben nog steeds te maken met complexen, omdat de complexe verzameling alle andere numerieke verzamelingen omvat. Maar we komen in een andere subcategorie terecht:
| complex getal | koninklijke partij | verbeelding deel | Subcategorie |
| 2+5i | 2 | 5i | Complex |
| 4 | 4 | 0 | puur koninklijk |
| 3i | 0 | 3i | Puur verbeelding |
Als we een puur reëel getal hebben, aangezien de denkbeeldige waarde b gelijk is aan nul, is het resterende complexe getal gelijk aan:
z = een + 0i = een
Aan de andere kant, als we pure verbeelding hebben, is a gelijk aan nul en bijgevolg blijft het complexe getal als volgt:
z = 0 + bi = bi
Grafische weergave van complexe getallen
Om complexe getallen weer te geven, gebruiken we het complexe vlak . Die bestaat uit twee lijnen : de echte lijn en de denkbeeldige lijn. Deze twee getallenlijnen worden gebruikt om de getallen in elke set grafisch te lokaliseren en als we ze samenvoegen, krijgen we een plan, zoals:

De X-as wordt de echte as genoemd, omdat daar de echte onderdeelwaarden zich bevinden. Hoewel de Y-as de denkbeeldige as wordt genoemd, worden hier de denkbeeldige waarden geschreven. Laten we een voorbeeld bekijken, we plaatsen het getal 3 + 2i in het complexe vlak.

Zoals je in de afbeelding zag, hebben we het getal gelokaliseerd met behulp van de getallen 3 en 2 als coördinaten, elk voor een as. Als je meer wilt weten over het weergeven van complexe getallen, raden we je aan dit artikel te lezen.
Wat zijn de soorten complexe getallen?
Nu zullen we zien op welke manieren we een complex getal kunnen uitdrukken. Tot nu toe hebben we alleen de basisvorm gezien (de binomiale vorm genoemd), die als een som is geschreven: reëel deel plus imaginair deel.
Maar in werkelijkheid hebben we drie vormen: de binominale, de polaire en de trigonometrische . Elk type uitdrukking heeft zijn eigenschappen en wordt in de ene of de andere situatie gebruikt. We gaan ze dus allemaal uitleggen en laten zien hoe je van de een naar de ander kunt gaan.
1. Binomiale vorm
Complexe getallen in binomiale vorm worden geschreven als de som van het reële deel en het imaginaire deel: a + bi. Het getal 6 + i is bijvoorbeeld een complex uitgedrukt in binominale notatie. In deze is de formule altijd hetzelfde:

Om een complex getal in binomiale vorm uit te drukken, hoeft u daarom alleen de werkelijke waarde en de denkbeeldige waarde ervan te kennen.
De waarde 3 + 2i heeft bijvoorbeeld de binomiale vorm en wordt, zoals we eerder zagen, als volgt weergegeven:

De binomiale vorm wordt voornamelijk gebruikt om het optellen en aftrekken van complexe getallen op te lossen.
2. Polaire vorm
Om complexe getallen in polaire vorm uit te drukken, moeten we hun module |z| berekenen en zijn betoog. De polaire vorm wordt voornamelijk gebruikt als we vermenigvuldiging en deling van complexe getallen moeten oplossen.
Om de modulus van het complexe getal te berekenen , voert u eenvoudigweg de modulus van a en b uit, zoals uitgelegd in de volgende formule:

En om het argument of de hoek van z te berekenen , moeten we de boogtangens van b tussen a berekenen:

Het is belangrijk op te merken dat om de waarde van hoek α precies te bepalen, het noodzakelijk is om te identificeren in welk kwadrant deze zich bevindt. De boogtangensfunctie berekent namelijk alleen hoeken tussen π/2 en -π/2. Om aan te geven in welk kwadrant het complexe getal zich bevindt, moeten we naar de waarden a en b kijken (of ze positief of negatief zijn):
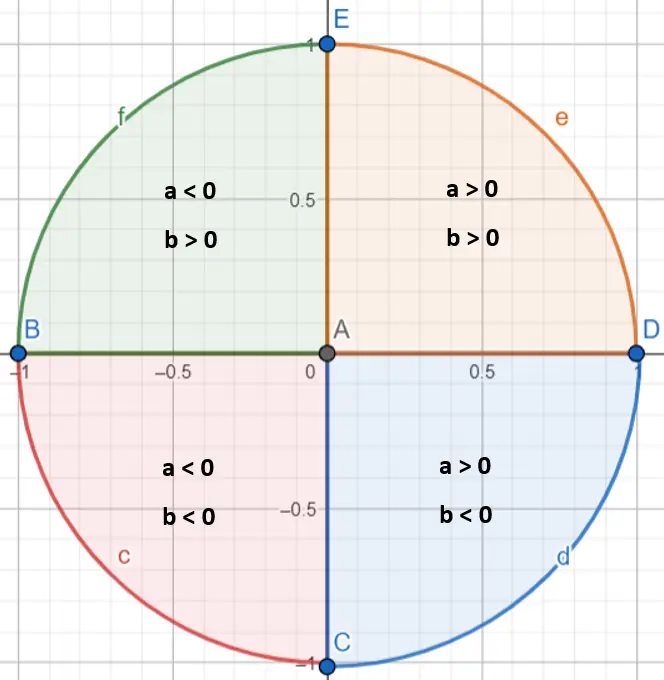
Zodra we weten in welk kwadrant ons getal valt, moeten we een paar regels volgen:
- Als het complexe getal zich in het eerste kwadrant bevindt (a > 0 en b > 0), laten we het argument ongewijzigd.
- Als het complexe getal zich in het tweede kwadrant bevindt (a < 0 en b > 0), voegen we π toe aan het argument.
- Als het complexe getal zich in het derde kwadrant bevindt (a < 0 en b < 0), trekken we π af van het argument.
- Als het complexe getal zich in het vierde kwadrant bevindt (a > 0 en b < 0), voegen we 2π toe aan het argument.
Als u niet weet waar we het over hebben als we kwadrant zeggen, raden we u aan ons artikel over trigonometrische verhoudingen te raadplegen.
Zodra we de grootte en het argument van z kennen, kunnen we het complexe getal in polaire vorm uitdrukken. Hoewel dit formulier verschillende nomenclaturen accepteert, zijn de twee belangrijkste:

Als we bijvoorbeeld het getal 3 + 5i in polair willen veranderen, hoeven we alleen maar de volgende procedure te volgen.
We berekenen eerst de module:
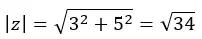
Vervolgens berekenen we het argument, dat zich in het eerste kwadrant bevindt, zodat het blijft zoals we het hebben berekend.
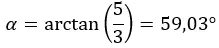
En we drukken het getal uit in polaire vorm:
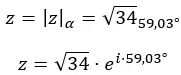
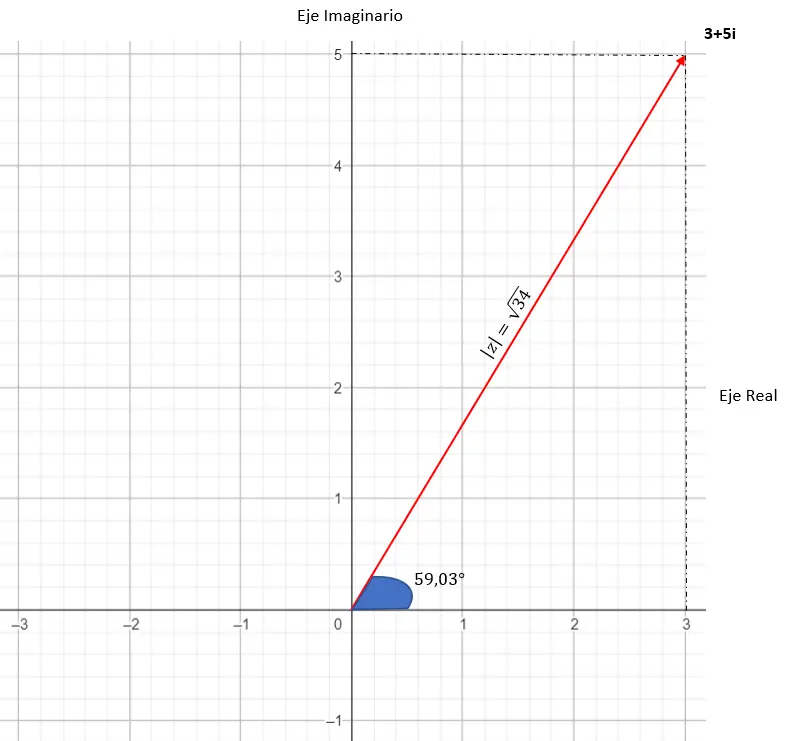
De grafische weergave is als volgt:
3. Trigonometrische vorm
Ten slotte hebben we de trigonometrische notatie , die wordt berekend op basis van de formule van Euler :

Om bijvoorbeeld het getal 4 – 3i in trigonometrische vorm uit te drukken, volgen we de volgende procedure:
We beginnen met het berekenen van de modulus en het argument met de formules die we in de polaire vormsectie hebben gebruikt.
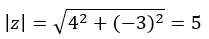
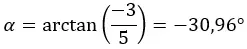
LET OP: Het argument bevindt zich in het vierde kwadrant, omdat (a > 0 en b < 0).
We voegen de gegevens in trigonometrische vorm toe aan de vergelijking.
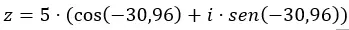
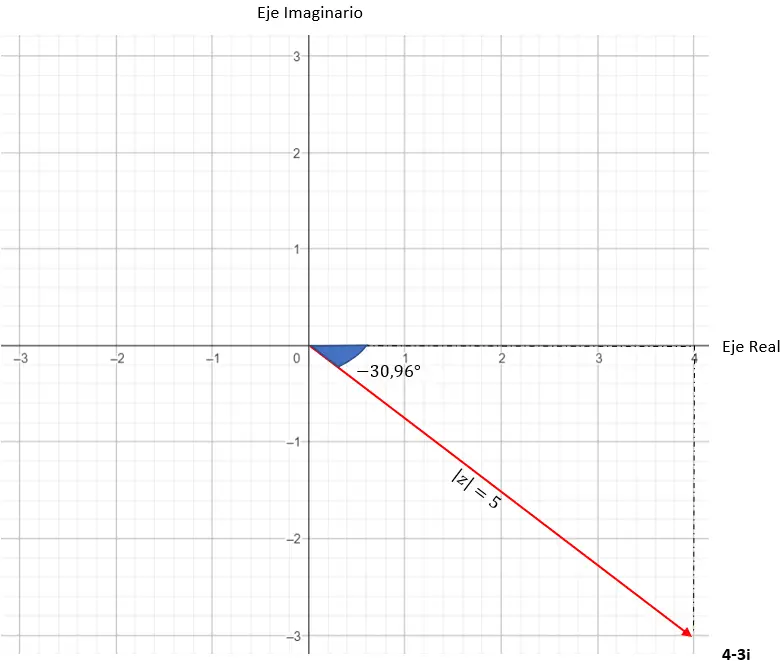
En we hebben het getal al uitgedrukt in trigonometrische vorm. De grafische weergave is als volgt.
Hoe kan ik van het ene type naar het andere overstappen?
Je kent nu alle manieren om een complex getal uit te drukken. En in de laatste sectie heb je kunnen zien hoe je toegang krijgt tot elk van deze, maar voordat we klaar zijn willen we een korte samenvatting geven van hoe je van het ene formulier naar het andere kunt gaan. Alleen jij hoeft de formules te gebruiken die we in de vorige sectie hebben gezien.
Van binomiale naar polaire vorm en omgekeerd
Om van binomiaal naar polair te gaan, stellen we het volgende diagram voor:
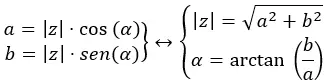
We hebben eerder een voorbeeld gezien waarin we van binomiaal naar polair gingen, dus nu gaan we van polair naar binomiaal met behulp van het bovenstaande diagram. We moeten √41 38,66 omzetten naar een binomiaal.
We berekenen eerst de a.
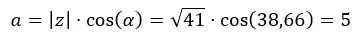
Dan berekenen we b.
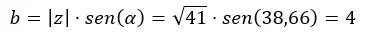
En we drukken het uit in binomiale vorm.
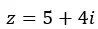
De grafische weergave van dit getal ziet er als volgt uit:
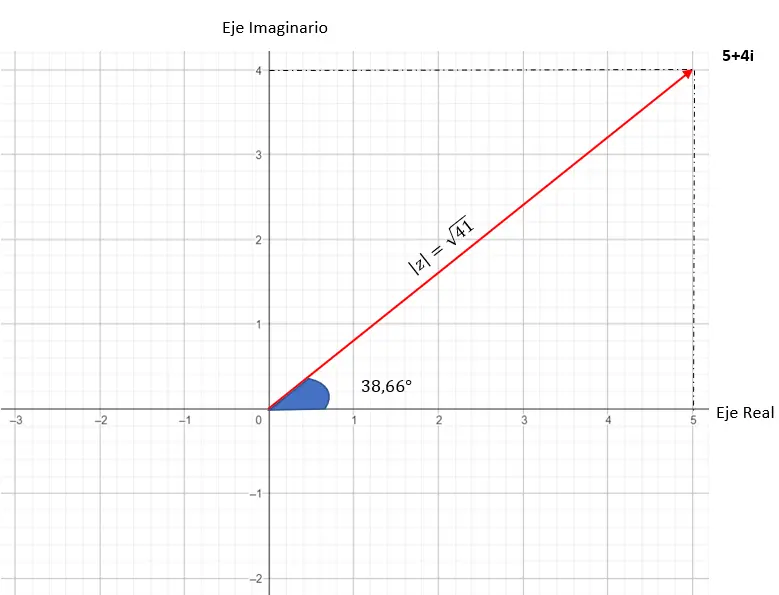
Van binominale vorm naar trigonometrische vorm en omgekeerd
Om van binomiaal naar trigonometrisch te gaan, moet je ook de formules toepassen waar we het in de vorige sectie over hadden. Op deze manier berekenen we eerst de modulus en het argument, en vervolgens plaatsen we deze gegevens in de vergelijking van de trigonometrische vorm. Om een voorbeeld te geven: we zullen het getal z = 3 + 2i trigonometrisch doorgeven.
We berekenen eerst de modulus en het argument.
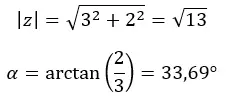
LET OP: Het argument bevindt zich in het eerste kwadrant, omdat (a > 0 en b > 0).
Vervolgens voltooien we de trigonometrische vormvergelijking met deze gegevens.
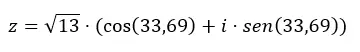
En als we van trigonometrisch naar binomiaal willen gaan, hoeven we alleen maar de vorige uitdrukking op te lossen.
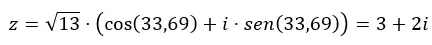
Van polaire vorm naar trigonometrische vorm en omgekeerd
Ten slotte gaan we van polaire vorm naar trigonometrische vorm. Dat is vrij eenvoudig, omdat deze twee vormen worden uitgedrukt door dezelfde twee waarden: modulo en argument . U hoeft dus alleen maar de formulieren in te vullen en dat is alles.
Laten we een voorbeeld geven, we zullen het getal z = √85 12,53 omzetten in trigonometrische vorm.
We herformuleren de twee variabelen (module en argument) in de vergelijking van de trigonometrische vorm:
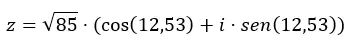
Dus nu je weet hoe je van de ene vorm naar de andere kunt overgaan, raden we je aan om een beetje te oefenen met een paar oefeningen . Op deze manier consolideer je de kennis die je in dit artikel hebt geleerd. Als u vragen heeft over dit onderwerp, kunt u deze achterlaten in de reacties. En als je meer wilt weten over complexe getallen, bekijk dan de onderstaande links.