Complexe getallen zijn een verzameling bestaande uit reële getallen endenkbeeldige getallen . Deze laatste twee numerieke sets kunnen grafisch worden weergegeven met behulp van de echte lijn en de denkbeeldige lijn. En wanneer we beide lijnen in hetzelfde vlak plaatsen, ontstaat het bekende complexe vlak.
Wat is het complexe plan?
Het complexe vlak wordt gevormd door de reële as (X-as), die equivalent is aan de echte lijn, en aan de andere kant de denkbeeldige as (Y-as), die de denkbeeldige lijn conceptualiseert.
Opgemerkt moet worden dat dit plan alle complexe getallen omvat. Daarom, hoe klein of klein het ook is, of in welke vorm een complex getal ook is geschreven, het kan grafisch op het plan worden weergegeven. Laten we eens kijken hoe deze getallen worden weergegeven in het complexe vlak.
Hoe complexe getallen in het complexe vlak te tekenen?
Zoals we al weten (of als je het niet weet, raden we je aan ons artikel over complexe getallen te lezen), zijn er drie manieren om een complex te schrijven: de binomiale vorm, de polaire vorm en de trigonometrische vorm. Elk drukt de complexe waarde uit volgens een andere structuur, dus de te volgen methode voor het maken van de grafische weergaven is anders.
Vervolgens leggen we uit welke procedure in de drie gevallen moet worden gevolgd:
Weergave in binominale vorm
Als we een complex getal in binomiale notatie hebben, wat het meest voorkomt, moeten we naar de structuur van het getal kijken:

waarbij a het reële deel is en b het denkbeeldige deel.
Als we dit weten, leiden we af dat de waarde van a degene is die we gebruiken voor de abscis (reële as) en dat de waarde van b degene is die we gebruiken voor de computer (denkbeeldige as). Met het volgende voorbeeld zul je het beter begrijpen.
We zullen proberen het getal weer te geven: 3 + 2i.
Het eerste is om de grafiek te tekenen (merk op dat de horizontale as de echte is en de verticale as de denkbeeldige):

Vervolgens lokaliseren we het punt van de grafiek in cartesiaanse coördinaten (x, y), die we afleiden uit het complexe getal. In dit praktische voorbeeld is ons punt (3, 2).
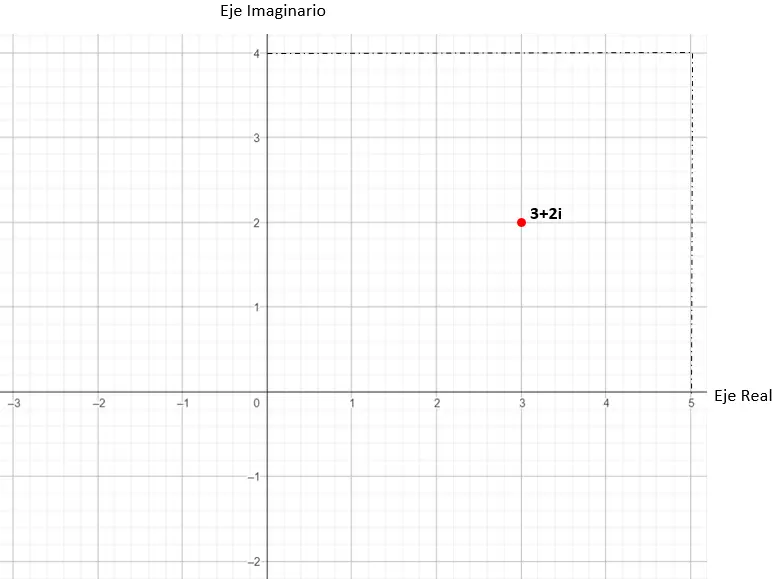
De waarde 3 + 2i zou dus in het complexe vlak worden weergegeven.
Vertegenwoordiging in polaire vorm
We zullen nu zien hoe een complex getal in polaire vorm wordt weergegeven. Om deze methode volledig te begrijpen, moet je weten dat polaire notatie een complex getal definieert op basis van de module en het argument. Die in de grafische weergave als poolcoördinaten worden gebruikt (en niet als cartesiaanse coördinaten!).
En het belangrijkste kenmerk van het polaire coördinatensysteem is dat de locatie van een punt wordt beschreven door middel van een vector en een hoek (niet zoals de vorige methode). Dat komt overeen met de module en het argument van complexe getallen. Vervolgens laten we u de universele formule zien voor de polaire vorm van een complex getal:

Waar |z| is de modulus en α is het argument. Deze twee variabelen worden in het plan vertaald door:
- Module: het is de lengte die een vector definieert (tussen de oorsprong en het punt dat overeenkomt met ons getal).
- Argument: is de hoek die de vector maakt met de X-as.
Daarom komt de modulus van een complex getal overeen met de lengte van de vector die we gebruiken om de grafiek te maken. Terwijl het argument of de hoek van het complexe getal de hoek is tussen de vector en de X-as. Hieronder ziet u een diagram waarin alle variabelen zijn geplaatst :
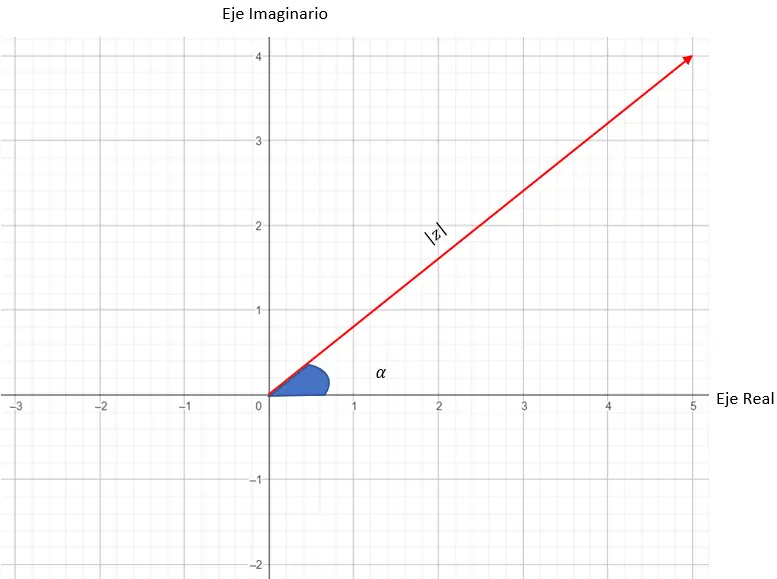
Nu zullen we proberen het getal weer te geven: 3 45 .
Eerst moeten we de module en het argument identificeren:
- Module: 3.
- Argument: 45 graden.
Vervolgens moeten we de punten in de grafiek vinden met een modulus gelijk aan 3, in dit geval zal elk punt op een cirkel met straal 3 werken.
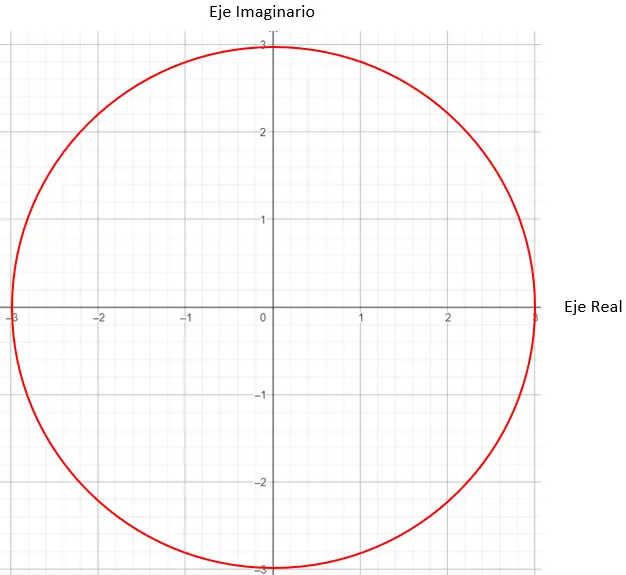
En om het exacte punt te bepalen, moeten we de voorwaarde stellen dat de door de module gegenereerde vector en de oorsprong een hoek van 45 graden moeten maken met de X-as.
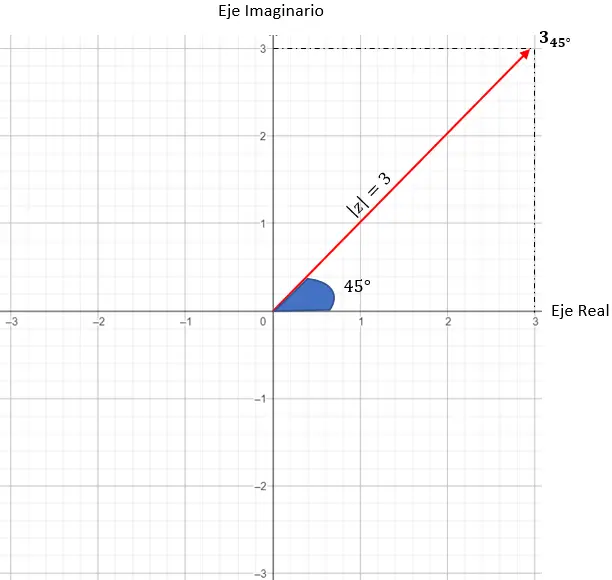
En we hebben al een complex getal weergegeven in polaire notatie.
Vertegenwoordiging in trigonometrische vorm
Ten slotte moeten we nog uitleggen hoe een complex getal in trigonometrische vorm wordt weergegeven. Dit geval en het vorige zijn praktisch hetzelfde, omdat de polaire vorm en de trigonometrische vorm dezelfde gegevens gebruiken om een complex getal uit te drukken: de modulus en het argument. Dit verandert alleen de structuur van de uitdrukking:

Waar, |z| is de modulus en α is het argument.
We moeten daarom profiteren van dezelfde methode als in het vorige geval: gebruik de module als “lengte” en het argument als hoek. Door het volgende voorbeeld te zien, zult u het beter begrijpen.
We stellen z = 4 · (cos (45) + i · sin(45)) voor.
Het eerste is om de module en de hoek te identificeren:
- Module: 4.
- Argument: 45 graden.
Vervolgens moeten we de punten in de grafiek vinden die een modulus gelijk aan 4 hebben, in dit geval zal elk punt op een cirkel met straal 4 werken.
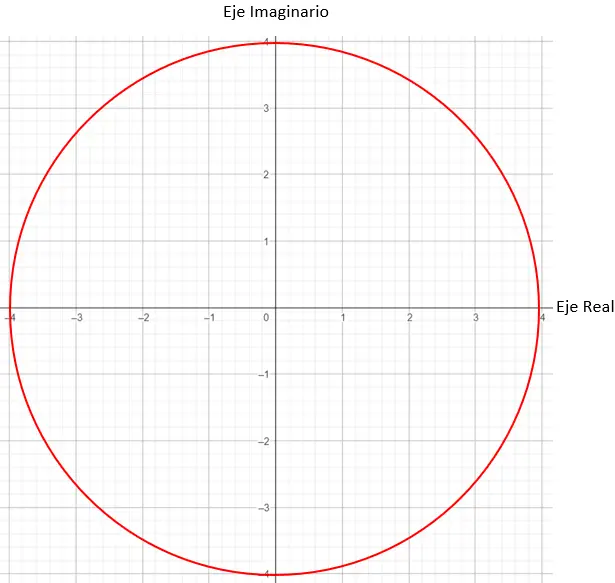
En ten slotte lokaliseren we het exacte punt, waarbij we vereisen dat de hoek gevormd tussen de modulusvector en de X-as 45 graden is, zoals het argument ons vertelt.
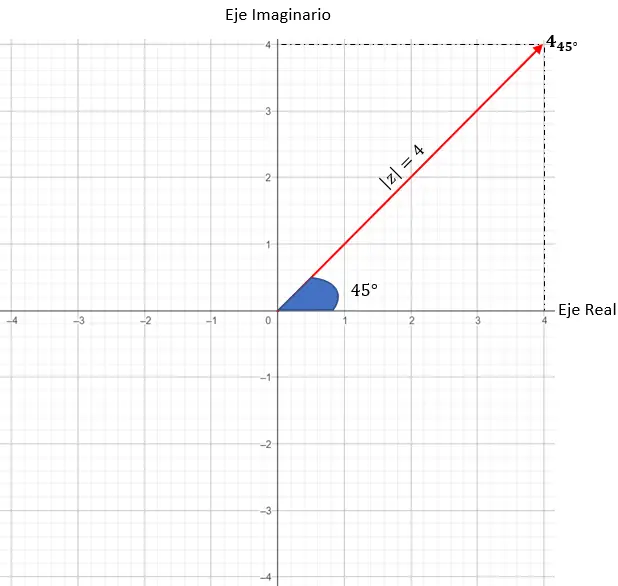
En dus vertegenwoordigen we een complex getal in trigonometrische vorm.
Complexe vliegtuigoefening
Ter afsluiting van deze publicatie bieden we nog een laatste oefening aan. We raden u ten zeerste aan het probleem op te lossen, omdat u op deze manier de kennis die in dit artikel wordt uitgelegd, consolideert.
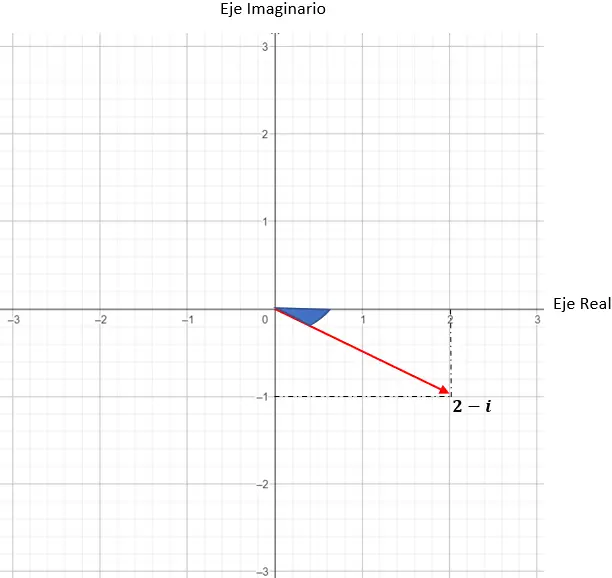
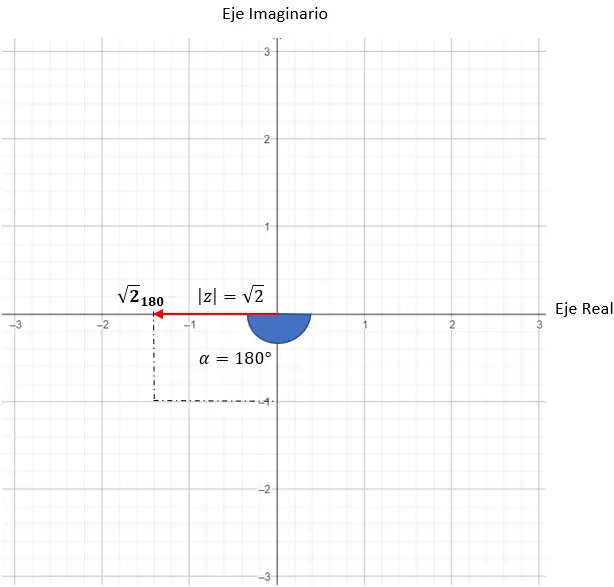
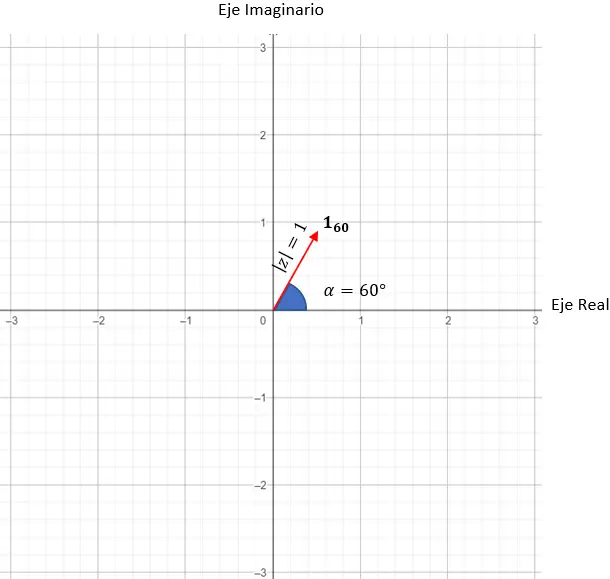
Bewijs van de grafische weergave van de volgende drie complexe getallen op het complexe vlak:
z = 2 – ik
w = √2180
p = cos(60) + ik zonde(60)