Complexe, geconjugeerde en getransponeerde matrix

Op deze pagina ziet u wat complexe matrices, geconjugeerde matrices en geconjugeerde transponeringsmatrices zijn. Nu lijken ze veel op jou, maar je zult zien hoe je aan het einde van de pagina het verschil tussen beide volledig zult begrijpen. Daarnaast zullen we voorbeelden zien van elk type en zijn eigenschappen.

complexe matrix

Laten we, voordat we de uitleg van de geconjugeerde matrix en de geconjugeerde matrix transponeren, het concept van complexe matrix bekijken:

Wat is een complexe matrix?

Een complexe matrix is een matrix die een bepaald complex aantal elementen heeft.

Bedenk dat een complex of denkbeeldig getal een getal is dat bestaat uit een reëel deel en een denkbeeldig deel, wat wordt aangegeven door de letter i. Bijvoorbeeld:

$3+5i$

Voorbeelden van complexe matrices

Laten we eens kijken naar enkele voorbeelden van complexe multidimensionale arrays:

Voorbeeld van een complexe matrix van orde 2 × 2

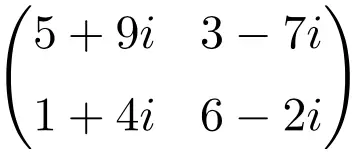
Voorbeeld van een complexe matrix met afmeting 3×3

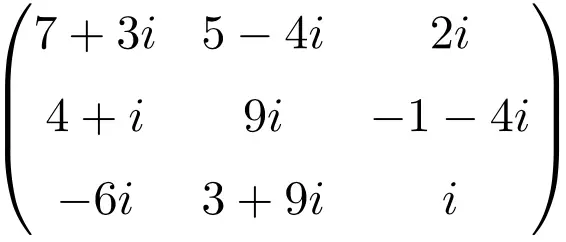
Voorbeeld van een complexe matrix van grootte 4×4

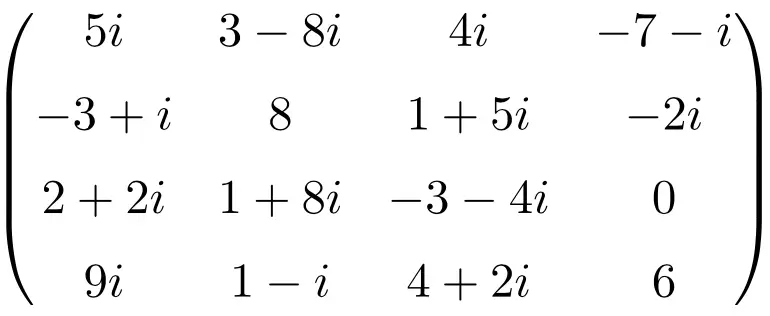
geconjugeerde matrix

Als we eenmaal hebben gezien wat de definitie van een complexe matrix is, gaan we kijken wat een geconjugeerde matrix en een getransponeerde geconjugeerde matrix zijn:

Wat is een geconjugeerde matrix?

Een geconjugeerde matrix is een complexe matrix waarin al zijn elementen zijn vervangen door hun conjugaten, dat wil zeggen dat het teken van het denkbeeldige deel van al zijn complexe getallen is veranderd.

De geconjugeerde matrix van

$A$

wordt uitgedrukt door een horizontale balk erboven:

$\overline{A}$

Voorbeeld van een geconjugeerde matrix

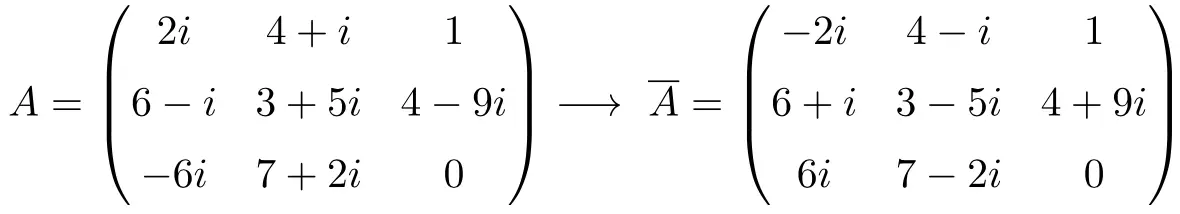
voorbeeld van matrixconjugaat, hoe een matrix te conjugeren

Eigenschappen van de geconjugeerde matrix

De kenmerken van dit type matrix zijn als volgt:

Het conjugaat van een geconjugeerde matrix is de oorspronkelijke matrix.

$\displaystyle \overline{\bigl( \ \overline{A} \vphantom{A^{9^1}} \ \bigr)} = A$

Het optellen (of aftrekken) van twee matrices en het conjugeren van het resultaat is hetzelfde als het eerst afzonderlijk conjugeren van de twee matrices en ze vervolgens optellen (of aftrekken).

$\displaystyle \overline{\bigl( A \pm B \bigr)} = \overline{A} \pm \overline{B}$

Het geconjugeerde product van twee matrices is gelijk aan het afzonderlijk conjugeren van de twee matrices en het vervolgens berekenen van de matrixvermenigvuldiging.

$\displaystyle \overline{\bigl( A \cdot B \bigr)} = \overline{A} \cdot \overline{B}$

Het vermenigvuldigen van een matrix met een scalair en het conjugeren van het resultaat is hetzelfde als eerst de conjugaten van de scalair en de matrix uitvoeren en vervolgens het product oplossen.

$\displaystyle \overline{\bigl( k \cdot A \bigr)} = \overline{k} \cdot \overline{A}$

Het transponeren van een matrix en deze vervolgens conjugeren betekent eerst de matrix conjugeren en deze vervolgens transponeren.

$\displaystyle \overline{\bigl(A^t \bigr)} = \left( \overline{A}\right)^t$

Het omgekeerde van een matrix doen en deze vervolgens conjugeren, is hetzelfde als de matrix conjugeren en vervolgens omkeren.

$\displaystyle \overline{\bigl( A^{-1} \bigr)} = \left(\overline{A} \right)^{-1}$

De rangorde van een geconjugeerde matrix is gelijk aan de rangorde van dezelfde ongeconjugeerde matrix.

$\displaystyle rg\left(\overline{A}\right) =rg(A)$

Het is onverschillig om het spoor van een geconjugeerde matrix te berekenen of om het spoor van dezelfde matrix zonder conjugatie te berekenen en vervolgens het resultaat te conjugeren.

$\displaystyle tr\left(\overline{A}\right) =\overline{tr(A)}$

Ten slotte komt het nemen van de determinant van een geconjugeerde matrix neer op het berekenen van de conjugaat van het resultaat van de determinant van dezelfde matrix zonder conjugatie.

$\displaystyle det\left(\overline{A}\right) = \overline{det(A)}$

Geconjugeerde transpositiematrix

Laten we, nadat we hebben gezien hoe we een matrix kunnen conjugeren, verder gaan met het concept van een geconjugeerde transpositiematrix:

Wat is een geconjugeerde transponeer- (of transponeer-) matrix?

De getransponeerde (of getransponeerde) conjugaatmatrix is die verkregen nadat een matrix is getransponeerd en vervolgens zijn conjugaat is gemaakt.

Dit type matrix wordt ook wel adjunct-matrix of eenvoudigweg adjunct-matrix genoemd. Bovendien wordt het meestal weergegeven met een asterisk

$(A^*)$

, hoewel er wiskundigen zijn die het tekenen als

$A^*$

$A^H$

Voorbeeld van een geconjugeerde transpositiematrix

Hier is een voorbeeld van het berekenen van de transpositie (of geconjugeerde transpositie) van een matrix:

$\displaystyle A=\begin{pmatrix}1+3i&2-i & -4i \\[1.1ex] 6 & 8+2i & 3-5i \\[1.1ex] 7i & 1+9i & -2+i\end{pmatrix}$

We transponeren eerst de matrix A:

$\displaystyle A^t=\begin{pmatrix}1+3i& 6 & 7i \\[1.1ex] 2-i & 8+2i & 1+9i \\[1.1ex] -4i & 3-5i & -2+i\end{pmatrix}$

En dan berekenen we de geconjugeerde matrix van de getransponeerde, of met andere woorden, we veranderen het teken van het imaginaire deel van alle complexe getallen:

$\displaystyle A^*=\overline{A^t}=\begin{pmatrix}1-3i& 6 & -7i \\[1.1ex] 2+i & 8-2i & 1-9i \\[1.1ex] 4i & 3+5i & -2-i\end{pmatrix}$

Daarom is de samenvatting van de berekening van de geconjugeerde transpositiematrix:

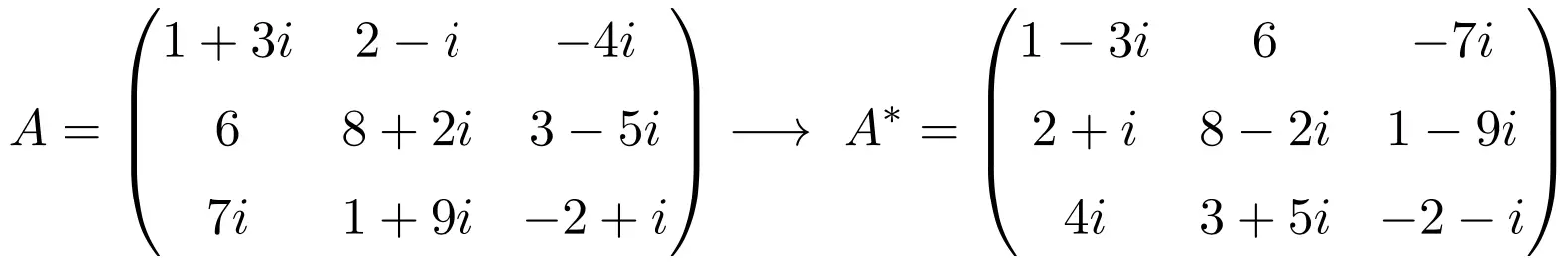
geconjugeerde transpositiematrix met dimensie 3x3

Eigenschappen van de geconjugeerde transpositiematrix

De eigenschappen van dit type vierkante matrix zijn als volgt:

De geconjugeerde getransponeerde matrix van een eerder getransponeerde en geconjugeerde matrix is de oorspronkelijke matrix.

$\displaystyle \bigl(A^*\bigr) ^* = A$

De opteleigenschap van geconjugeerde transpositiematrices stelt dat het optellen (of aftrekken) van twee matrices en het vervolgens toepassen van deze bewerking op het resultaat gelijkwaardig is aan het eerst uitvoeren van de geconjugeerde transpositie van elke matrix en vervolgens het optellen (of aftrekken) van de resultaten.

$\displaystyle \bigl( A\pm B \bigr)^* = A^*\pm B^*$

Het vermenigvuldigen van twee matrices en vervolgens hun geconjugeerde transpositie geeft hetzelfde resultaat als het inverse product van de geconjugeerde transponeringsmatrices.

$\displaystyle \bigl( A\cdot B \bigr)^* = B^*\cdot A^*$

Het berekenen van de geconjugeerde transpositiematrix van het product van een scalair en een matrix is hetzelfde als het conjugeren van het complexe getal en het afzonderlijk vinden van de geconjugeerde transpositie van de matrix en vervolgens vermenigvuldigen.

$\displaystyle \bigl( k\cdot A \bigr)^* = \overline{k}\cdot A^*$

Als de matrix inverteerbaar is, is de volgorde waarin de matrixinversie en de geconjugeerde transpositiebewerkingen worden uitgevoerd niet relevant.

$\displaystyle \bigl( A^{-1} \bigr)^*= \bigl( A^* \bigr)^{-1}$