Op deze pagina leggen we uit wat een coördinatensysteem is en daarnaast vind je alles over het cartesiaanse coördinatensysteem. Je zult ook andere soorten coördinatensystemen zien (polair, cilindrisch, bolvormig, enz.) en praktische toepassingen van een coördinatensysteem.
Wat is een coördinatensysteem?
Hoewel het in eerste instantie wat moeilijk is om dit concept te begrijpen, is de definitie van een coördinatensysteem:
Een coördinatensysteem is een systeem waarmee we de positie van een punt kunnen identificeren. Dat wil zeggen, het is een reeks waarden die worden gebruikt om de locatie van elk geometrisch object te definiëren.
De positie waarin het volgende vliegtuig vliegt, kan bijvoorbeeld worden beschreven door een coördinatensysteem:
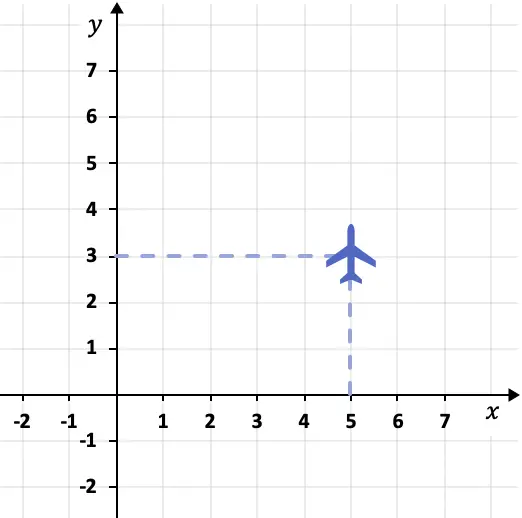
In dit geval bevindt het vlak zich op punt (5.3). Omdat de X-coördinaat 5 is en de Y-coördinaat 3.
![]()
Aan de andere kant wordt het punt (0,0) de coördinatenoorsprong genoemd, omdat dit het punt is waar de coördinatenassen beginnen en het het referentiepunt is van het coördinatensysteem.
Uit nieuwsgierigheid wordt aangenomen dat de wiskundige die het coördinatensysteem heeft uitgevonden de Fransman René Descartes was. En daarom wordt het ook wel het Cartesiaanse coördinatensysteem genoemd.
Cartesisch coördinatensysteem in het vlak
De grafiek die we in de vorige sectie zagen, behoort tot het cartesiaanse coördinatensysteem in het vlak. We zeggen dat het zich in het vlak bevindt omdat het een tweedimensionaal systeem is, dat wil zeggen dat het slechts twee assen heeft: de X-as en de Y-as.
De X-as komt overeen met horizontale coördinaten, terwijl de Y-as verticale coördinaten vertegenwoordigt. Hieronder ziet u verschillende punten grafisch weergegeven met hun coördinaten:
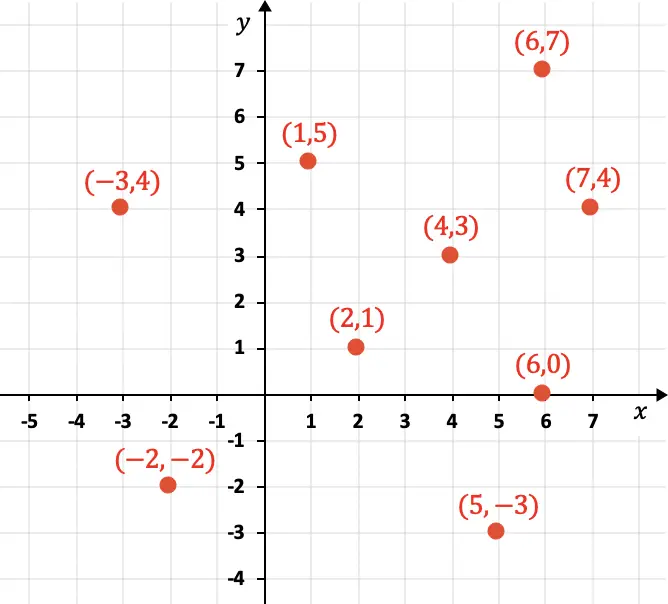
Zoals je in de grafiek kunt zien, worden de coördinaten numeriek weergegeven tussen haakjes, daarnaast wordt de X-component eerst geplaatst en vervolgens de Y-component: (4,3). Bovendien kunnen coördinaten positief, negatief of nul zijn.
Aan de andere kant wordt dit type coördinatensysteem ook wel Cartesisch vlak genoemd.
Ten slotte moet je weten dat coördinaatassen op verschillende manieren kunnen worden gezegd, hoewel ze allemaal hetzelfde betekenen:
- De X-as wordt ook wel de abscis-as of OX-as genoemd.
- De Y-as wordt ook wel de y-as of OY-as genoemd.
Cartesisch coördinatensysteem in de ruimte
We hebben zojuist gezien hoe je een punt in het vlak kunt weergeven, dat wil zeggen in een coördinatensysteem met twee assen (2 dimensies). De werkelijkheid bestaat echter uit 3 dimensies (hoogte, breedte en diepte).
In de Euclidische meetkunde wordt de driedimensionale ruimte dus over het algemeen weergegeven door een coördinatensysteem met drie assen, allemaal loodrecht op elkaar:
- De X-as vertegenwoordigt diepte.
- De Y-as geeft de breedte aan.
- De Z-as komt overeen met de hoogte.
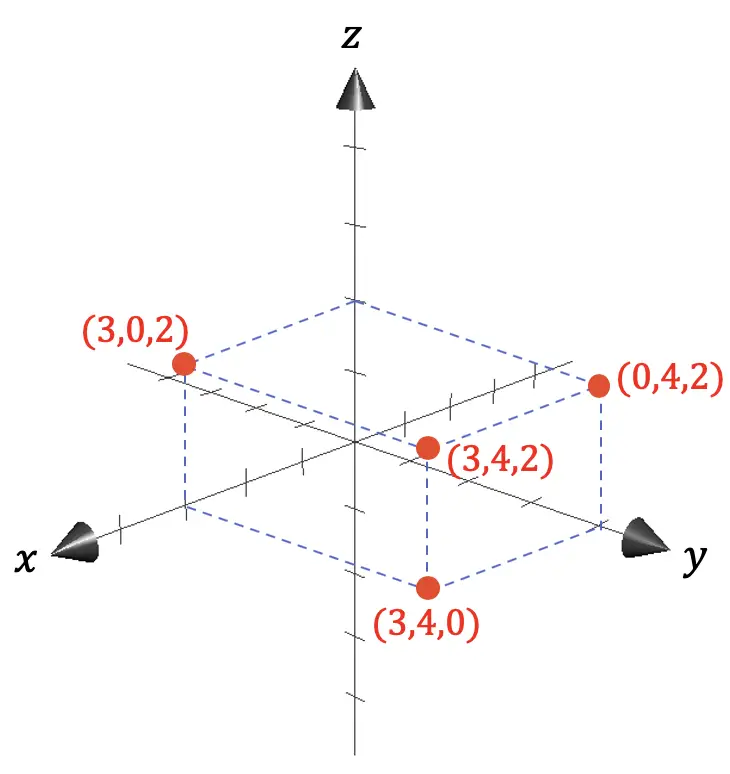
Zoals je in de vorige grafische weergave kunt zien, worden de coördinaten van elk punt gegeven door de projecties op de assen van de afstanden tussen het betreffende punt en de oorsprong (0,0,0).
polair coördinatensysteem
Cartesische coördinatensystemen, 2D of 3D, worden het meest gebruikt. Maar in sommige gevallen kan het voor ons handig zijn om een ander type coördinatensysteem te gebruiken.
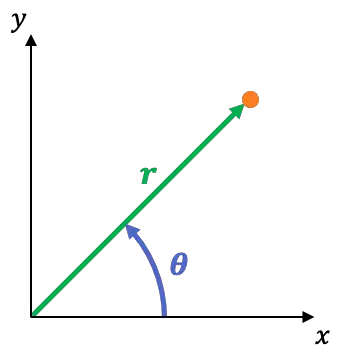
Het polaire coördinatensysteem is een tweedimensionaal referentiesysteem waarvan de coördinaten zijn:
-

is de afstand tussen de coördinaatoorsprong en het punt. Dit wordt de radiale coördinaat genoemd.
-

is de hoek die de X-as maakt met de lijn die door het punt en de oorsprong gaat. Dit wordt een hoek- of azimutale coördinaat genoemd.
U kunt eenvoudig overschakelen van het rechthoekige coördinatensysteem naar het polaire coördinatensysteem met behulp van de volgende vergelijkingen:
Converteer poolcoördinaten naar cartesiaanse coördinaten
![]()
![]()
Overschakelen van cartesische coördinaten naar poolcoördinaten
![]()
![]()
Cilindrisch coördinatensysteem
Het cilindrische coördinatensysteem lijkt sterk op het polaire coördinatensysteem. In feite is het hetzelfde, maar met nog een coördinaat: hoogte.
Het cilindrische frame is dus een driedimensionaal frame, dat wil zeggen met 3 coördinaten:
-

is de orthogonale projectie van het punt in het XY-vlak, of met andere woorden, de afstand van het punt tot de Z-as.
-

is de hoek die de positieve halve as maakt

-

is de hoogte van het punt, is dezelfde coördinaat van het cartesiaanse coördinatensysteem in de ruimte.
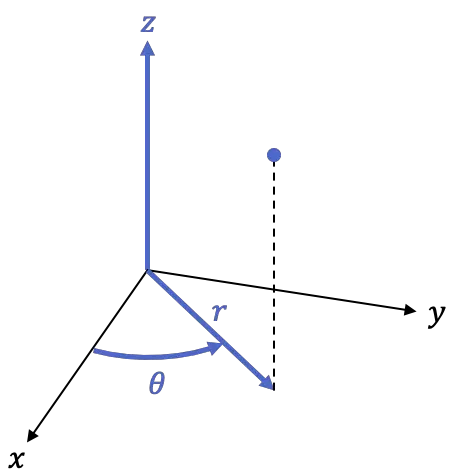
De volgende formules worden gebruikt om het cartesiaanse coördinatensysteem om te zetten in cilindrische coördinaten:
Converteer cilindrische coördinaten naar cartesische coördinaten
![]()
![]()
![]()
Converteer cartesische coördinaten naar cilindrische coördinaten
![]()
![]()
![]()
Sferisch coördinatensysteem
Ten slotte hebben we het bolvormige coördinatensysteem. Dit type coördinatensysteem lijkt ook behoorlijk op poolcoördinaten en cilindrische coördinaten, hoewel er uiteraard enkele verschillen van bestaan.
Het bolvormige coördinatensysteem is een systeem voor het beschrijven van driedimensionale Euclidische ruimtes en heeft daarom drie coördinaten:
-

is de afstand (in R3) van de oorsprong tot het punt.
-

is de hoek die het positieve deel van de X-as maakt met de lijn

geprojecteerd in het XY-vlak.
-
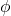
is de hoek tussen het positieve deel van de Z-as en de lijn

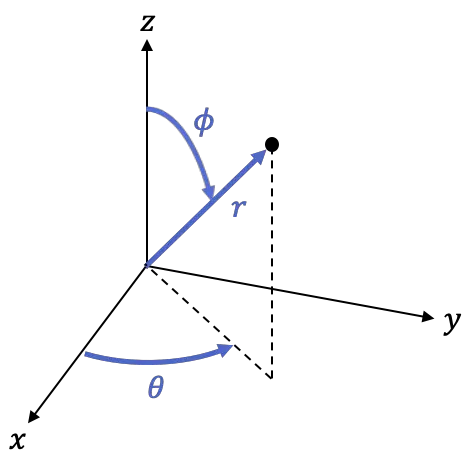
U kunt schakelen tussen sferische en cartesiaanse coördinaten met behulp van de volgende formules:
Sferische coördinaten omzetten in cartesiaanse coördinaten
![]()
![]()
![]()
Cartesische coördinaten omzetten in sferische coördinaten
![]()
![]()
Real-world toepassingen van het coördinatensysteem
Coördinatensystemen zijn zo belangrijk in de wiskunde omdat ze ook in het echte leven worden gebruikt. Ze zijn bijvoorbeeld handig voor het lokaliseren van objecten, mensen of zelfs plaatsen op een kaart. In feite bestaat GPS vanwege coördinatensystemen, omdat ze dat gebruiken om je positie op aarde te kennen.
Om precies te zijn: de geografische coördinaten van GPS bestaan uit twee elementen: breedtegraad en lengtegraad. Breedtegraad (noord of zuid) en lengtegraad (oost of west) zijn twee hoekcoördinaten die de hoek meten tussen het middelpunt van de aarde en uw locatie. Beide worden uitgedrukt in graden, in decimale of sexagesimale coördinaten.