Canonieke, segmentale of symmetrische vergelijking van de lijn

Hier vind je de uitleg van wat de formule voor de canonieke (of segmentale) vergelijking van de lijn, ook wel symmetrische vergelijking genoemd, is. Daarnaast krijg je voorbeelden te zien en te oefenen met opgeloste oefeningen. En je zult zelfs ontdekken hoe de canonieke vergelijking wordt berekend op basis van de algemene (of impliciete) vergelijking van de lijn.

Wat is de canonieke of segmentale vergelijking van de lijn?

Bedenk dat de wiskundige definitie van een lijn een reeks opeenvolgende punten is die in dezelfde richting worden weergegeven, zonder krommen of hoeken.

De canonieke vergelijking van de lijn , ook wel de segmentvergelijking van de lijn genoemd, is dus een manier om elke lijn wiskundig uit te drukken. Om dit te doen, is het voldoende om de snijpunten met de coördinaatassen van de genoemde lijn te kennen.

Aan de andere kant wordt in de analytische meetkunde de canonieke (of segmentale) vergelijking van de lijn ook wel de symmetrische vergelijking van de lijn genoemd.

Formule van de canonieke of segmentale vergelijking van de lijn

De canonieke of segmentale vergelijking van de lijn is de algebraïsche uitdrukking van de lijn die kan worden bepaald door de waarden te kennen waar de lijn de x-as en de y-as snijdt.

Als een lijn de cartesische assen op de volgende punten snijdt:

Snijpunt met de X-as:

$(a,0)$

Snijpunt met de Y-as:

$(0,b)$

De formule voor de canonieke (of segmentale) vergelijking van de lijn is:

$\cfrac{x}{a}+ \cfrac{y}{b}= 1$

segmentale of symmetrische canonieke vergelijking van de lijn in de ruimte

Opgemerkt moet worden dat er in geen van de volgende drie gevallen sprake is van een canonieke (of segmentale) vergelijking van de lijn:

Wanneer de lijn verticaal is, dat wil zeggen evenwijdig aan de OY-as. Omdat de vergelijking van een verticale lijn is
$x=k.$
Wanneer de lijn horizontaal is, dat wil zeggen evenwijdig aan de OX-as. Omdat de vergelijking van een horizontale lijn is
$y=k.$
Wanneer de lijn door de coördinaatoorsprong (punt
$(0,0)$

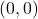
), omdat we dan twee onbepaaldheden in de vergelijking van de lijn zouden hebben.

Voorbeeld van hoe u de canonieke of segmentale vergelijking van de lijn kunt vinden

Om u het concept beter te laten begrijpen, zullen we een segmentaal (of canoniek) vergelijkingsprobleem van de lijn oplossen:

Zoek de canonieke of segmentale vergelijking van de lijn die door de volgende twee punten gaat:

$A(0,4) \qquad \qquad B(-2,0)$

In dit geval geeft de verklaring ons niet 2 punten, maar eerder de twee snijpunten met de assen.

Snijpunt van de lijn met de X-as:

$(-2,0)$

Snijpunt van de lijn met de Y-as:

$(0,4)$

Omdat we dus de twee snijpunten met de assen al kennen, hoeven we alleen maar de formule voor de canonieke of segmentale vergelijking van de lijn toe te passen:

$\cfrac{x}{a}+ \cfrac{y}{b}= 1$

En ten slotte vervangen we de waarde van de parameters

$a$

$b$

in de formule:

$\cfrac{\bm{x}}{\bm{-2}}\bm{+} \cfrac{\bm{y}}{\bm{4}}\bm{= 1}$

Je weet nu wat de canonieke (of segmentale) vergelijking van de lijn is. U moet echter weten dat er andere manieren zijn om een lijn uit te drukken, en daarvan valt de expliciete vergelijking op. Dit type lijnvergelijking is moeilijk volledig te begrijpen, daarom hebben we er alles over in detail uitgelegd op de gelinkte pagina.

Bereken de canonieke of segmentale vergelijking van de lijn op basis van de algemene vergelijking

We hebben zojuist een manier gezien om de canonieke of segmentale vergelijking van de lijn te bepalen, maar er zijn ook andere methoden:

De canonieke of segmentale vergelijking van een lijn kan worden verkregen uit de algemene (of impliciete) vergelijking van dezelfde lijn:

$Ax+By+C=0$

Eerst veranderen we van kant bij de coëfficiënt C:

$Ax+By=-C$

Vervolgens delen we de hele vergelijking door de waarde van de teken-veranderde parameter C:

$\cfrac{Ax+By}{-C}=\cfrac{-C}{-C}$

$\cfrac{Ax}{-C}+\cfrac{By}{-C}=1$

En via de eigenschappen van breuken komen we tot de formule voor de canonieke of segmentale vergelijking van de lijn:

$\cfrac{x}{-\frac{C}{A}}+\cfrac{y}{-\frac{C}{B}}=1$

Uit deze formule volgt dus dat de termen

$a$

$b$

van de canonieke vergelijking van een lijn zijn gelijkwaardig aan de volgende uitdrukkingen:

$a= -\cfrac{C}{A} \qquad \qquad b= -\cfrac{C}{B}$

Opgeloste problemen van de canonieke of segmentale vergelijking van de lijn

Oefening 1

Wat zijn de snijpunten met de coördinaatassen van de volgende lijn?

$\cfrac{x}{3}+ \cfrac{y}{-1}= 1$

zie oplossing

De lijn in de oefening wordt uitgedrukt in de vorm van een canonieke of segmentale vergelijking van de lijn, waarvan de formule is:

$\cfrac{x}{a}+ \cfrac{y}{b}= 1$

Daarom zijn de punten waar de lijn de coördinaatassen snijdt:

Snijpunt met de X-as:

$\bm{(3,0)}$

Snijpunt met de Y-as:

$\bm{(0,-1)}$

Oefening 2

Wat is de canonieke of segmentale vergelijking van de getekende lijn?

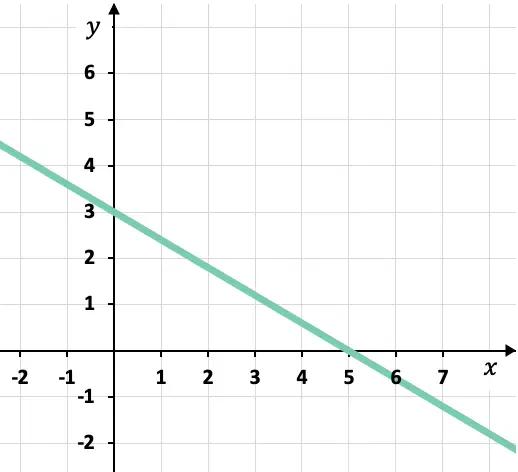
segmentale of symmetrische canonieke vergelijking in het vlak

zie oplossing

Uit de grafiek kunnen we de punten weten waar de lijn de coördinaatassen kruist:

Snijpunt van de lijn met de X-as:

$(5,0)$

Snijpunt van de lijn met de Y-as:

$(0,3)$

Dus zodra we de twee snijpunten met de assen al kennen, hoeven we alleen maar de formule te gebruiken voor de canonieke of segmentale vergelijking van de lijn:

$\cfrac{x}{a}+ \cfrac{y}{b}= 1$

En ten slotte vervangen we de waarde van de parameters

$a$

$b$

in de formule:

$\cfrac{\bm{x}}{\bm{5}}\bm{+} \cfrac{\bm{y}}{\bm{3}}\bm{= 1}$

Oefening 3

Bereken de canonieke of segmentale vergelijking van de lijn die wordt bepaald door de volgende algemene (of impliciete) vergelijking:

$3x-2y+6=0$

zie oplossing

Om van een algemene vergelijking naar een segmentvergelijking te gaan, moeten we eerst de onafhankelijke term van de vergelijking isoleren:

$3x-2y+6=0$

$3x-2y=-6$

Ten tweede delen we de hele vergelijking door de coëfficiënt aan de rechterkant van de vergelijking:

$\cfrac{3x-2y}{-6}=\cfrac{-6}{-6}$

$\cfrac{3x}{-6}+\cfrac{-2y}{-6}=\cfrac{-6}{-6}$

De bovenstaande uitdrukking komt overeen met het volgende:

$\cfrac{x}{\frac{-6}{3}}+\cfrac{y}{\frac{-6}{-2}}=1$

Zodat de canonieke, segmentale of symmetrische vergelijking van de lijn is:

$\cfrac{\bm{x}}{\bm{-2}}\bm{+} \cfrac{\bm{y}}{\bm{3}}\bm{= 1}$

Oefening 4

Bepaal de canonieke of segmentale vergelijking waarvan de richtingsvector is

$\vv{\text{v}}=(4,-3)$

en gaat door het punt

$P(-1,5).$

zie oplossing

We vinden eerst gemakkelijk de continue vergelijking van de lijn vanuit zijn richtingsvector en een punt dat bij de lijn hoort:

$\cfrac{x-P_1}{\text{v}_1} = \cfrac{y-P_2}{\text{v}_2}$

$\cfrac{x-(-1)}{4} = \cfrac{y-5}{-3}$

$\cfrac{x+1}{4} = \cfrac{y-5}{-3}$

Laten we nu de algemene vergelijking van de lijn berekenen door de breuken kruislings te vermenigvuldigen en de resulterende termen te groeperen:

$-3(x+1) = 4(y-5)$

$-3x-3 = 4y-20$

$-3x-3 - 4y+20 =0$

$-3x - 4y+17 =0$

Het is daarom voldoende om de algemene vergelijking van de lijn om te zetten in een canonieke vergelijking. Om dit te doen, verwijderen we eerst de onafhankelijke term uit de vergelijking:

$-3x - 4y=-17$