Het vereenvoudigen van breuken of het verkleinen van breuken is een wiskundige procedure die tot doel heeft een complexe breuk om te zetten in een andere, eenvoudiger gelijkwaardige breuk . Daarom kunnen we hierdoor de onherleidbare fractie van de oorspronkelijke uitdrukking vinden, en dit kan op verschillende manieren worden gedaan. Voordat we ze uitleggen, raden we je echter aan om de rekenmachine uit te proberen om breuken te vereenvoudigen, die je net onder deze tekst kunt vinden.
Online breuk vereenvoudigen
Met de volgende rekenmachine om breuken online te vereenvoudigen, kunt u gemengde getallen van elk type verkleinen. U hoeft eenvoudigweg de waarden van de teller en de noemer in te voeren en vervolgens op de knop Vereenvoudigen te klikken. Zodra je dat hebt gedaan, krijg je de meest vereenvoudigde uitdrukking.
Hoe een breuk vereenvoudigen?
Zoals we eerder zeiden, impliceert het vereenvoudigen van breuken het vinden van de onherleidbare fractie van een complexere breuk. Momenteel hebben we twee methoden om breuken te vereenvoudigen: de eerste is het gebruik van normale delingen en de tweede is het extraheren van een gemeenschappelijke deler.
Vereenvoudig breuken door te delen
Dit systeem bestaat uit het delen van zowel de teller als de noemer tussen gemeenschappelijke delers (behalve 1) totdat we geen gemeenschappelijke deler meer hebben, op deze manier krijgen we een onherleidbare breuk. Hoewel we bij het kiezen van de deler die we bij elke deling gaan gebruiken, dit op twee verschillende manieren kunnen doen: de eerste is door gemeenschappelijke delers te gebruiken totdat we de eenvoudigste vorm van die breuk verkrijgen, en de tweede is door de grootste gemene deler van de teller en de noemer.
Als we bijvoorbeeld de breuk 12/64 willen vereenvoudigen, kunnen we dat doen door de teller en de noemer te delen door de gcf van beide, of door beide delen van de breuk door hetzelfde getal te delen totdat we een onherleidbare breuk krijgen, te beginnen met de kleinste delers (1 niet meegerekend) en naar boven toe werkend. Hieronder zie je beide methoden stap voor stap opgelost:
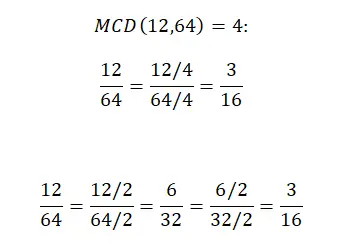
Vereenvoudiging van breuken door extractie van gemeenschappelijke factoren
Om deze andere methode uit te voeren, zullen we de teller en de noemer moeten ontbinden in priemgetallen . En we zullen de originele numerieke waarden vervangen door het product van gelijkwaardige machten . Vervolgens gaan we verder met het reduceren van de uitdrukking door de machten te vereenvoudigen met een gemeenschappelijke basis, waarbij we de eigenschappen van de machten gebruiken. We zullen nu een voorbeeldbreuk vereenvoudigen met behulp van deze methode:
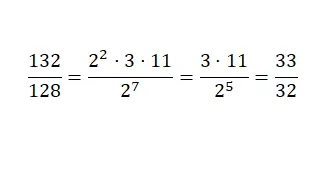
Breuken die moeilijk te verkleinen zijn
Vervolgens zullen we enkele twijfels oplossen met betrekking tot de meest complexe gevallen van vereenvoudiging, op deze manier kunt u elke fractie die u wordt voorgesteld, verminderen. Hoewel dit gedeelte nogal optioneel is, kunt u, als u wilt beginnen met oefenen, doorgaan naar het laatste gedeelte:
Breuken vereenvoudigen met exponenten
Om dit soort breuken te vereenvoudigen, moeten we de exponent-expressie als een enkele numerieke waarde schrijven. Ten eerste kunnen we priemfactorisatie proberen, waarbij we de teller en de noemer vereenvoudigen. En als we dan nog geen onherleidbare breuk hebben verkregen, gaan we verder met het delen van de twee delen van de breuk totdat we een uitdrukking krijgen die niet langer kan worden gereduceerd. Zoals je kunt zien, impliceert het vereenvoudigen van breuken met machten het combineren van alle methoden waar we het in de vorige sectie over hadden.
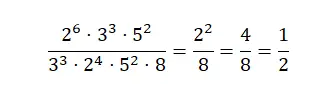
vereenvoudig negatieve breuken
Als we negatieve breuken willen vereenvoudigen, kunnen we dat doen met een van de drie eerder uitgelegde methoden, aangezien het teken geen directe invloed heeft op de berekeningsprocedure . U hoeft slechts één wijziging in het resultaat aan te brengen, namelijk door het minteken toe te voegen. Maar al het andere is precies hetzelfde. Zodat u het kunt zien, laten we u hieronder het eerste voorbeeld zien dat we opgelost hebben uitgelegd, maar met een minteken.
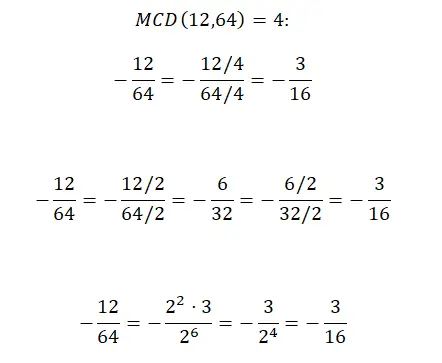
Breuken vereenvoudigen met grote getallen
In dit geval raden we aan de extractiemethode met gemeenschappelijke factoren te gebruiken, omdat grote getallen gemakkelijker worden als je ze in priemfactoren uitdrukt. Zo voorkom je dat je veel delingen moet oplossen totdat je bij een onherleidbare breuk uitkomt. Hoewel je in werkelijkheid elke methode kunt gebruiken die je verkiest.
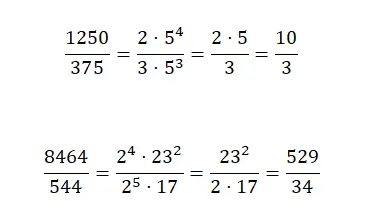
Hoe breuken vereenvoudigen met de wetenschappelijke rekenmachine?
In veel wetenschappelijke rekenmachines kunnen we elke breuk die we willen op een eenvoudiger manier uitdrukken, zolang deze maar niet onherleidbaar is. In het geval van de wetenschappelijke rekenmachines van Casio (het meest voorkomende merk onder studenten) moeten we op de knop drukken die is gemarkeerd met de volgende uitdrukking "S⇔D". Hierdoor zullen we alle soorten uitdrukkingen kunnen vereenvoudigen , inclusief breuken . Bij andere merken zijn er ook manieren om dit te doen, maar je zult dit moeten raadplegen in de handleiding van jouw model, aangezien de te volgen procedure enigszins kan variëren.

Opgeloste oefeningen voor het vereenvoudigen van breuken
Hier volgen enkele oefeningen om breuken te vereenvoudigen, waarmee je de verschillende methoden kunt oefenen die we hebben uitgelegd. We raden u aan het theoretische deel met hetzelfde belang te volgen als de praktijk, omdat u dankzij dit deel de wiskundige concepten die bij dit soort oefeningen betrokken zijn, perfect zult begrijpen.
Oefening 1
Vereenvoudig de volgende breuken totdat je de onherleidbare breuk vindt:
In de volgende afbeelding vindt u vier breuken vereenvoudigd met behulp van een van de drie methoden. Hoewel u, wanneer u ze zelf probeert te verminderen, dit kunt doen met de methode die u verkiest, is het belangrijkste dat u het juiste resultaat krijgt, dat u moet vergelijken met het resultaat dat we u in de correctie laten zien:

Oefening 2
Bereken de waarde van x in de volgende breukvergelijkingen:
We geven nu twee vergelijkingen met breuken, die door vereenvoudiging kunnen worden opgelost. Dit is een iets ingewikkelder oefening, maar door enkele wiskundige basisconcepten toe te passen, naast de concepten die we in dit artikel hebben uitgelegd, kun je deze eenvoudig oplossen.
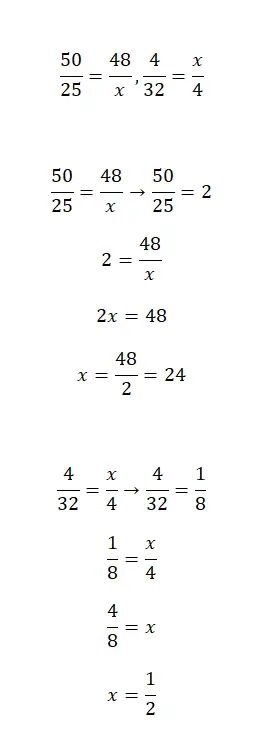
Oefening 3
Bereken de equivalente onherleidbare breuken van elk van de onderstaande breuken:
Nu dagen we je uit om deze breuken zoveel mogelijk te vereenvoudigen, terwijl je ze oplost, zul je zien dat ze iets moeilijker zijn dan de vorige. Omdat de ene een negatief teken bevat, bevat de andere grote numerieke waarden en een andere bevat machten.

Als je meer oefeningen over breuken wilt, raden we je aan deze laatste link in te voeren, daar vind je veel problemen en bewerkingen met breuken. Waarmee je alle concepten met betrekking tot breuken kunt oefenen.