Breuken of gemengde getallen zijn numerieke uitdrukkingen die de ene hoeveelheid aangeven gedeeld door de andere. Het is daarom een waarde die wordt weergegeven door het quotiënt van twee getallen. Met dit soort getallen kunnen we decimale en gehele getallen uitdrukken en zelfs verhoudingen aangeven. Vervolgens zullen we breuken op een meer wiskundige manier definiëren en u enkele voorbeelden laten zien, zodat u dit concept grafisch begrijpt.
Wat zijn breuken?
Een breuk is gelijk aan het aantal delen dat we nemen van een eenheid die in gelijke delen is verdeeld. Grafisch wordt het dus weergegeven door twee termen, gescheiden door een horizontale lijn in het midden. Om precies te zijn: bovenaan de regel vinden we de teller en onder de noemer.
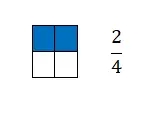
Zoals u kunt zien, zijn breuken een heel eenvoudig wiskundig concept om in een grafiek te tekenen , omdat ze hand in hand gaan met verhoudingen. Daarom hebben we in het vorige voorbeeld het aantal gekleurde vierkantjes uitgedrukt met een breukgetal.
Fractionele termen
De twee delen van de breuk zijn:
- Teller: Deze term bevindt zich boven de horizontale lijn en hier schrijven we het aantal stukken dat we nemen. We kunnen positieve, negatieve en nul (gelijk aan nul) tellers vinden.
- Noemer: Deze andere term bevindt zich onder de lijn en hier schrijven we het totale aantal delen waarin de eenheid is verdeeld. We kunnen positieve en negatieve noemers vinden, maar deze kunnen niet nul zijn.
soorten breuken
Er zijn veel soorten breuken, afhankelijk van de getallen waaruit ze bestaan en de gelijkwaardigheid die ze met andere breuken hebben. Vervolgens zullen we alle bestaande categorieën definiëren en commentaar geven op de kenmerken waarmee ze van de andere kunnen worden onderscheiden:
- Juiste breuken: zijn breuken die gevormd worden door een teller die kleiner is dan de noemer. Als je deze breuken omzet naar een decimaal getal , krijg je een getal tussen nul en één. Het kan niet groter zijn dan één, omdat de waarde van de teller altijd kleiner zal zijn dan die van de noemer en daarom zal de eenheid niet worden overschreden.
- Onjuiste breuken: zijn breuken met een teller die groter is dan de noemer, in dit geval drukken ze numerieke waarden uit die groter zijn dan één. Zo is 8/5 bijvoorbeeld gelijk aan 1,6, wat groter is dan 1. Dit is een andere manier om gemengde getallen uit te drukken, die van het volgende type zijn.
- Gemengde breuken: ook wel gemengde getallen genoemd, zijn breuken die bestaan uit een geheel getal en een gemengd getal. In principe worden ze weergegeven met de gehele waarde vóór de breuk, dus om ze om te zetten in onechte breuken moet je het gehele deel vermenigvuldigen met de noemer, het optellen bij de teller en de noemer hetzelfde laten.
- Decimale breuken: zijn breuken met een noemer die een hoeveelheid uitdrukt die gelijk is aan een macht van tien, bijvoorbeeld: 6/10, 34/1000 of 5/100. Deze worden gebruikt in decimale notatie en komen het meest voor bij het converteren van exacte decimale getallen naar gemengde getallen. We zullen dit in meer detail bespreken in de volgende sectie.
- Samengestelde breuken: zijn breuken die zijn samengesteld uit een andere breuk, hetzij in de teller, hetzij in de noemer, of in beide. Om deze uitdrukkingen te vereenvoudigen en als één breuk weer te geven, moeten we de teller delen door de noemer. Dit zal duidelijker worden zodra we de verdeling tussen breuken uitleggen.
- Equivalente breuken: zijn breuken die gelijkwaardig zijn aan hetzelfde getal, ook al bestaan ze niet uit dezelfde tellers of noemers. Bijvoorbeeld: 8/4 = 4/2 = 2, beide breuken zijn gelijk aan twee. In dit specifieke geval komt dat doordat de eerste breuk gelijk is aan tweemaal de tweede en daarom een proportionele relatie handhaaft.
- Onherleidbare breuken: dit zijn breuken die niet verder kunnen worden vereenvoudigd, omdat de teller en de noemer geen gemeenschappelijke factoren hebben en daarom door geen enkel getal kunnen worden gedeeld. Enkele voorbeelden van dit type zijn onder andere: 9/5, 5/6, 7/8. Om te weten hoe je ze kunt detecteren, is het belangrijk om te weten hoe je de grootste gemene deler kunt berekenen .
Bewerkingen met breuken
Nu we de verschillende categorieën breuken kennen die er bestaan, zullen we zien hoe we de verschillende rekenkundige bewerkingen met gemengde getallen kunnen oplossen. Opgemerkt moet worden dat dit iets ingewikkelder is dan bewerkingen met gehele getallen, hoewel alles vrij eenvoudig is als je de methodologie eenmaal begrijpt. Bovendien leggen we niet alleen de theorie uit, maar laten we je ook enkele voorbeelden zien. Dat gezegd hebbende, laten we aan de slag gaan.
som van breuken
Het optellen van breuken met een gemeenschappelijke noemer is vrij eenvoudig, omdat je gewoon de twee tellers bij elkaar optelt en de noemer hetzelfde laat. Aan de andere kant wordt het optellen van breuken met verschillende noemers een beetje lastig, omdat je het kleinste gemene veelvoud van de noemers moet vinden. En dan moeten we het product van elke teller optellen door de lcm (de nieuwe noemer) te delen door de oude noemer. Om het beter te begrijpen, kunt u het volgende diagram bekijken:
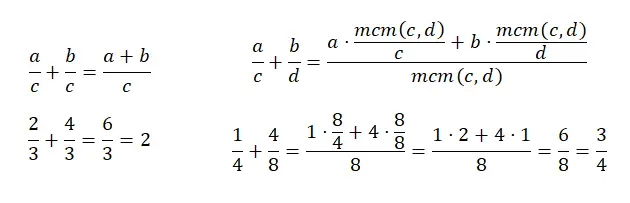
aftrekken breuken
Het aftrekken van breuken met een gemeenschappelijke noemer lijkt erg op optellen, in feite gebeurt alles op dezelfde manier, behalve in de som van de tellers, want in plaats van optellen moet je aftrekken. En bij het aftrekken van breuken met verschillende noemers gebeurt hetzelfde, het is praktisch hetzelfde, behalve dat we in plaats van het product van de tellers op te tellen door de lcm te delen door de oude noemer, moeten aftrekken. Hier is nog een diagram:
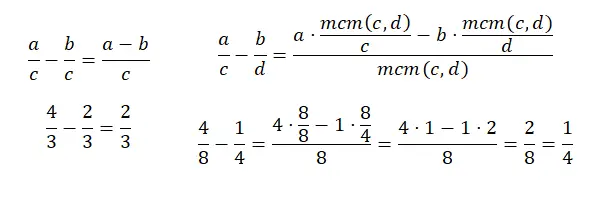
vermenigvuldigen van breuken
Het vermenigvuldigen van breuken kan op dezelfde manier worden opgelost, ongeacht of de noemers hetzelfde zijn of niet. Kortom, je moet de tellers met het ene deel vermenigvuldigen en de noemers met een ander deel. Dit is misschien wel de eenvoudigste handeling, aangezien u slechts twee vermenigvuldigingen hoeft uit te voeren.
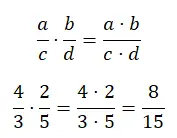
delen van breuken
Het verdelen in breuken is ook vrij eenvoudig op te lossen, je hoeft alleen maar de kruisjes te vermenigvuldigen. Met andere woorden: de teller is het resultaat van het vermenigvuldigen van de teller van de eerste breuk met de noemer van de tweede. terwijl de noemer het product is van de noemer van de eerste breuk en de teller van de tweede.
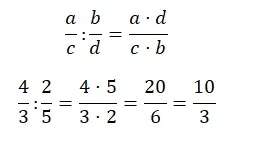
Vereenvoudig breuken
Het vereenvoudigen van breuken of het verkleinen van breuken is op zichzelf geen rekenkundige bewerking , maar het is erg belangrijk om te weten hoe je dat moet doen. Het is ook een onderwerp dat we al een beetje hebben behandeld met de soorten breuken. Om een gemengd getal te vereenvoudigen, moeten we dus de teller en de noemer door hetzelfde getal delen. Over het algemeen zullen we de grootste gemene deler kiezen om deze vereenvoudiging te bewerkstelligen. In de volgende afbeelding vindt u een voorbeeld.
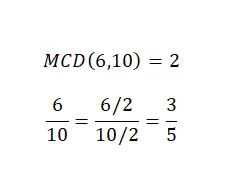
Zoals je kunt zien, hebben we twee equivalente breuken , dus beide vertegenwoordigen dezelfde numerieke waarde, maar de tweede is eenvoudiger dan de eerste. Daarom hebben we de vereenvoudigingsdoelstelling met succes bereikt.
Hoe ga je van decimaal naar breuk en omgekeerd?
De genererende breuk is de onherleidbare breuk die wordt verkregen uit een decimaal getal, een exact decimaal getal of een herhalend decimaal getal. Natuurlijk moeten we verschillende methoden gebruiken, afhankelijk van het type decimaal, die we hieronder zullen bespreken.
Converteer van exact decimaal naar genererende breuk
In dit geval kunnen we onze toevlucht nemen tot de decimale breuken waar we in het begin commentaar op gaven. We moeten eenvoudigweg de numerieke waarde in de teller schrijven, maar zonder de komma. Terwijl we in de noemer de macht van tien schrijven, die evenveel nullen heeft als er cijfers in de teller zijn.
Als we echter een decimaal getal groter dan één hebben, zoals 4,25, dan moeten we het aantal volledige eenheden dat we hebben vermenigvuldigen met de noemerwaarde en dit optellen bij de oorspronkelijke teller. Hieronder vindt u van elk type een voorbeeld:
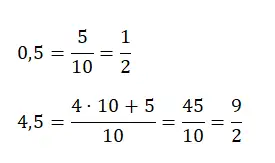
Converteer zuivere herhalende decimalen naar genererende breuken
Als we een puur periodiek decimaal getal hebben, zullen we, als we de genererende breuk willen krijgen, dezelfde waarde in de teller moeten zetten, maar zonder decimaalpunt, en het gehele deel ervan aftrekken. Hoewel de noemer gelijk zal zijn aan een getal dat uit slechts negens bestaat, moeten we specifiek evenveel negens schrijven als het aantal cijfers in het decimale deel van het oorspronkelijke getal. Dit systeem is enigszins verwarrend, maar met een paar voorbeelden zullen we het begrijpen:
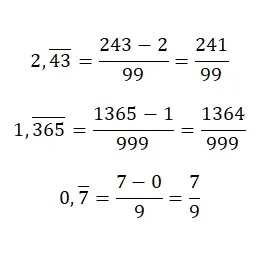
Converteer gemengde herhaalde decimalen naar het genereren van breuken
Als we een gemengd herhaald decimaal getal hebben, zullen we een vrij complexe regel moeten toepassen. Eerst schrijven we het getal zonder de komma in de teller en trekken we het gehele deel af, gevolgd door de niet-terugkerende decimalen, ook zonder de komma. Wat de noemer betreft, moet u net zoveel negens schrijven als er cijfers in het periodieke decimale deel zijn, gevolgd door evenveel nullen als er cijfers in het niet-terugkerende decimale deel zijn.
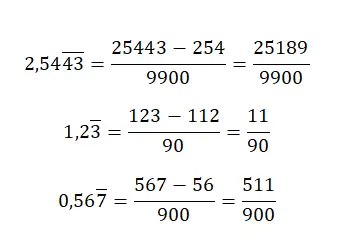
breuk omzetten naar decimaal
Om van een breuk naar een decimaal te gaan, deelt u eenvoudigweg de teller door de noemer, omdat een gemengd getal niets meer is dan het quotiënt tussen twee waarden . Dus door de deling op te lossen, krijg je het overeenkomstige decimale getal. In de volgende afbeelding vindt u enkele vrij eenvoudige voorbeelden:
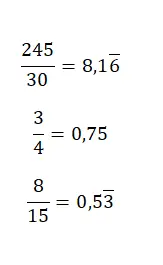
breuken oefeningen
Nu je alle theorie over breuken kent, raden we je aan enkele oefeningen te doen. Zo leer je alle begrippen dieper uitgelegd en ga je op de dag van het examen sneller verder met het oplossen van de berekeningen. Bovendien heb je alle soorten breukenoefeningen gezien die er bestaan en weet je hoe je ze dienovereenkomstig kunt oplossen. Tot slot wil ik u vertellen dat we ook een online breukcalculator tot uw beschikking hebben, waarmee u alle breukbewerkingen kunt oplossen.