Binomials - Mathority

Op deze pagina vindt u uitleg over wat een binominale term is en daarnaast kunt u van elk type binominale voorbeelden bekijken. We laten u ook de formules zien die worden gebruikt om bewerkingen met binominale getallen op te lossen: vermenigvuldiging van binomiale getallen, binomiale kwadraten, binominale kubussen,…

Wat is een paar?

In de algebra is de definitie van een binomiaal:

Een binomiaal is een polynoom dat uit slechts twee monomialen bestaat . Met andere woorden, een binomiaal bestaat uit een algebraïsche uitdrukking met slechts twee verschillende termen die worden samengevoegd door het plusteken (+) of het minteken (-).

Het woord binomiaal komt uit het Grieks en is samengesteld uit twee lexicale componenten ( bi en nomos ), die het volgende betekenen:

bi : voorvoegsel betekenis 2.
nomos : betekent deel.

We kunnen hieruit de betekenis van de binomiaal afleiden: polynoom met twee delen (of 2 monomialen).

Aan de andere kant heeft het concept van een paar een andere betekenis dan de wiskundige, namelijk dat een paar ook een stel van twee persoonlijkheden kan aanduiden die een leidende rol spelen in het politieke leven, in bepaalde sportdisciplines of zelfs in entertainment. . Maar uiteraard zullen we ons hier concentreren op de wiskundige definitie van de binominale waarde.

Voorbeelden van binomialen

Om het begrip binomiaal te begrijpen, zullen we verschillende voorbeelden van dit type polynoom zien:

Voorbeeld van een kwadratische binomiaal:

$x^2+4x$

Voorbeeld van een derdegraads binomiaal:

$x^3+5$

Voorbeeld van een binomiaal van de vierde graad:

$3x^4+8x^2$

Nu we weten wat een binominale term is, zullen we zien welke verschillende soorten binomiale getallen er zijn en hoe bewerkingen met binomiale getallen worden opgelost.

binomiaal kwadraat

Een kwadratische binomiaal is een opmerkelijke identiteit, ook wel een opmerkelijk product of opmerkelijke gelijkheid genoemd. Het oplossen van de macht van een binominale waarde verhoogd tot 2 hangt af van het feit of het een sombinominale of een verschilbinominale waarde is.

Een binominale som verwijst naar die binominale waarde waarvan de twee termen positief zijn, dat wil zeggen een binominale som is:

$(a+b)^2$

Aan de andere kant is een binomiaal verschil (of aftrekking) het conjugaat van de binomiaal van de optelling, dat wil zeggen dat een van zijn monomialen een negatief teken heeft. Daarom is de algebraïsche uitdrukking voor een kwadraat binomiaal verschil:

$(a-b)^2$

Om een kwadratische binomiaal te berekenen, moet je een formule toepassen die, zoals we hebben gezien, varieert afhankelijk van of het om een optelling of een aftrekking gaat. Ontdek hoe dit wordt gedaan in de formules voor opmerkelijke gelijkheden , waar u alle stapsgewijze uitleg, voorbeelden en opgeloste oefeningen kunt zien, en niet alleen van deze twee opmerkelijke gelijkheden, maar van ze allemaal.

binomiaal in blokjes

Hoewel ze minder vaak worden gebruikt, worden kubusbinomialen ook als opmerkelijke producten beschouwd. Of met andere woorden, er zijn wiskundige regels waarmee je snel de kubus van een binomiaal kunt vinden (je kunt ze zien in de link hierboven met opmerkelijke identiteitsformules ).

Net als voorheen hangt het resultaat van deze potentiëring ervan af of het de derde macht van een som is:

$(a+b)^3$

Of als de macht daarentegen wordt gevormd door de derde macht van een verschil of een aftrekking:

$(a-b)^3$

Logischerwijs is het belangrijkste verschil tussen een gekwadrateerde binominale en een kubusvormige binomiale de machtsexponent. De formule voor een kubusvormige binomiaal is echter veel ingewikkelder dan die voor een kwadratische binomiaal.

opmerkelijke overeenkomsten

Er zijn met name bepaalde soorten binominale namen die een beetje bijzonder zijn vanwege hun kenmerken, omdat ze overeenkomen met minder bekende opmerkelijke identiteiten (of opmerkelijke producten).

Som van de kwadraten:
$a^2+b^2$
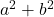
Verschil (of aftrekking) van vierkanten:
$a^2-b^2$
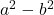
Som van kubussen:
$a^3+b^3$
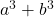
Verschil (of aftrekking) van kubussen:
$a^3-b^3$

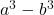
Goud

$a$

$b$

zijn twee monomialen.

Hoewel deze binomiale uitdrukkingen veel lijken op de uitdrukkingen die we hierboven zagen (binomiaal kwadraat en binomiaal kubusvormig), zijn ze, als je goed kijkt, verschillend. In die zin kun je ook de formules van opmerkelijke binomialen en hun afleidingen zien door op de bovenstaande link te klikken ⬆ formules van opmerkelijke identiteiten.⬆

binomiale vermenigvuldiging

Een van de meest voorkomende bewerkingen met binominale getallen is vermenigvuldiging. Vervolgens zien we een voorbeeld van hoe je een vermenigvuldiging tussen binomialen kunt berekenen.

$(x^2+2x)\cdot (x-5)$

Om de binominale vermenigvuldiging te berekenen, moeten we eerst elke term in de eerste binominale factor vermenigvuldigen met elke term in de tweede binomiale:

$x^2\cdot x+x^2\cdot (-5)+2x\cdot x +2x\cdot (-5)$

$x^3-5x^2+2x^2 -10x$

Vervolgens groeperen we vergelijkbare termen, dat wil zeggen dat ze hetzelfde letterlijke deel hebben:

$\bm{x^3-3x^2 -10x}$

En op deze manier zijn we erin geslaagd om het resultaat van het product tussen de paren te vinden.

Product van twee binomialen met een gemeenschappelijke term

Wanneer de binomialen die deelnemen aan de vermenigvuldiging als gemeenschappelijke term de variabele hebben

$x,$

Er is een formule om deze binomiale bewerking snel te berekenen:

$(x+a)(x+b) = x^2+(a+b)x+ab$

Hier laten we u een opgeloste oefening zien, zodat u kunt zien hoe u deze formule kunt toepassen:

$\begin{aligned} (x+4)(x+5) &= x^2+(4+5)x+4\cdot 5 \\[2ex] & = x^2+9x+20 \end{aligned}$

De binomiaal van Newton

De binomiale stelling van Newton , ook wel de binominale stelling genoemd, is een formule die wordt gebruikt om de machten van binomiale getallen te berekenen.

De wiskundige formule voor de binomiaal van Newton is als volgt:

$\displaystyle \left( a+b\right)^n = & \sum_{k=0}^{n}\begin{pmatrix} n\\ k\end{pmatrix}x^{n-k}y^k$

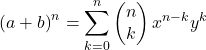
Of gelijkwaardig:

$\left( a+b\right)^n =\begin{pmatrix} n \\ 0 \end{pmatrix} \right)a^n b^0 + \begin{pmatrix} n \\ 1 \end{pmatrix} a^{n-1}b^{1} + \begin{pmatrix} n \\ 2 \end{pmatrix} a^{n-2}b^{2} + \dots + \begin{pmatrix} n \\ n \end{pmatrix} a^0 b^{n}$

Zoals u kunt zien, is deze formule een beetje ingewikkeld om te begrijpen. Dit is de reden waarom we de machten van de binomialen van de laagste graad hieronder hebben weergegeven, zodat je het beter kunt begrijpen:

formule voor de binominale stelling van Newton

Deze formule kan een beetje vervelend zijn bij het berekenen van binomialen in het kwadraat of in de kubus, omdat er, zoals we hierboven hebben gezien, eenvoudiger formules bestaan. De binomiaal van Newton is echter erg handig voor het vinden van machten van een hogere graad. Het wordt bijvoorbeeld veel gebruikt om een binomiaal tot de vierde te bepalen.

Maar om deze formule toe te passen, moet je weten hoe je een combinatorisch getal berekent, dat wil zeggen de algebraïsche uitdrukking van het type

$\begin{pmatrix} 4 \\ 2 \end{pmatrix}$

, berekening niet eenvoudig. 🔍 Daarom raden wij je aan om rechtsboven in onze zoekmachine te zoeken hoe dit moet 🔎, je vindt ons artikel waarin we deze handeling stap voor stap aan je uitleggen.