Bewerkingen met functies: optellen, aftrekken, product, delen en samenstelling

In dit artikel leggen we uit welke bewerkingen met functies kunnen worden uitgevoerd. U kunt de uitleg en opgeloste oefeningen over bewerkingen met functies bekijken. En tot slot vind je de eigenschappen van de bewerkingen bij de functies.

Wat zijn bewerkingen met functies?

U kunt 5 verschillende soorten bewerkingen uitvoeren met functies: optellen, aftrekken, product, delen en samenstelling. Dat wil zeggen dat twee functies kunnen worden opgeteld, afgetrokken, vermenigvuldigd, verdeeld of samengesteld.

Vervolgens zullen we zien hoe elk type bewerking wordt uitgevoerd met functies en de kenmerken van elk ervan.

Som van functies

De waarde van de som (of optelling) van twee functies is gelijk aan de som van de waarde van elke functie. Met andere woorden, om de afbeelding van een somfunctie te berekenen, voegt u eenvoudigweg de afbeeldingen toe van de functies die bij de bewerking betrokken zijn.

$(f+g)(x)=f(x)+g(x)$

Bovendien is het domein van de som van twee functies het snijpunt van het domein van elke gesommeerde functie.

$\text{Dom}(f+g)=\text{Dom}(f)\cap\text{Dom}(g)$

Laten we eens kijken hoe twee functies worden toegevoegd aan de hand van een voorbeeld:

$f(x)=x^2+1 \qquad g(x)=\log(x-1)$

We voegen eerst de twee functies toe:

$(f+g)(x)=f(x)+g(x)=x^2+1+\log(x-1)$

En nu vinden we het domein van de somfunctie. Om dit te doen, berekenen we het domein van elke functie afzonderlijk:

$\text{Dom}(f)=\mathbb{R}\qquad\text{Dom}(g)=(1,+\infty)$

➤ Zie: hoe je het domein van een functie berekent

Het domein van de functie die het resultaat is van de bewerking is dan:

$\text{Dom}(f+g)=\text{Dom}(f)\cap\text{Dom}(g)=(1,+\infty)$

Elke bewerking met functies moet vergezeld gaan van zijn domein om het resultaat volledig te definiëren.

Aftrekken van functies

Het beeld van de aftrekking (of het verschil) van twee functies is de aftrekking van de afbeeldingen van elke functie die aan de bewerking deelneemt:

$(f-g)(x)=f(x)-g(x)$

Net als bij de optelfunctie is het aftrekkingsdomein van twee functies gelijk aan het snijpunt van het domein van elke functie.

$\text{Dom}(f-g)=\text{Dom}(f)\cap\text{Dom}(g)$

Dus als een functie niet is gedefinieerd bij een bepaalde waarde van de onafhankelijke variabele x, zal de functie die voortvloeit uit de aftrekking ook niet worden gedefinieerd.

Laten we eens kijken hoe twee functies worden afgetrokken via een voorbeeld:

$f(x)=\sqrt{x}\qquad g(x)=\cfrac{3}{x-4}$

We trekken eerst de twee functies af:

$(f-g)(x)=f(x)-g(x)=\sqrt{x}-\cfrac{3}{x-4}$

En dan bepalen we het domein van de aftrekkingsfunctie:

$\text{Dom}(f)=[0,+\infty)\qquad\text{Dom}(g)=\mathbb{R}-\{4\}$

$\text{Dom}(f-g)=\text{Dom}(f)\cap\text{Dom}(g)=[0,4)\cup (4,+\infty)$

Vlaggenschipproduct

Om het product of (de vermenigvuldiging) van twee functies te berekenen, hoeft u alleen maar de uitdrukkingen van elke functie te vermenigvuldigen.

$(f\cdot g)(x)=f(x)\cdot g(x)$

Aan de andere kant is het domein van de productfunctie de verzameling snijpunten van het domein van elke vermenigvuldigde functie.

$\text{Dom}(f\cdot g)=\text{Dom}(f)\cap\text{Dom}(g)$

Als we bijvoorbeeld de volgende twee functies hebben:

$f(x)=\sqrt[3]{x^2-1}\qquad g(x)=\cfrac{2}{3x+6}$

Eerst voeren we de werking van het product uit met de twee functies:

$(f\cdot g)(x)=f(x)\cdot g(x)=\sqrt[3]{x^2-1}\cdot\cfrac{2}{3x+6}=\cfrac{2\sqrt[3]{x^2-1}}{3x+6}$

En ten slotte vinden we het domein van de functie die voortvloeit uit de bewerking:

$\text{Dom}(f)=\mathbb{R}\qquad\text{Dom}(g)=\mathbb{R}-\{-2\}$

$\text{Dom}(f\cdot g)=\text{Dom}(f)\cap\text{Dom}(g)=(-\infty,-2)\cup (-2,+\infty)$

Verdeling van functies

Het numerieke resultaat van een deling (of quotiënt) van twee functies komt overeen met de volgende vergelijking:

$\displaystyle\left(\frac{f}{g}\right)(x)=\frac{f(x)}{g(x)}$

Het domein van de deling van twee functies is echter de verzameling snijpunten van het domein van elke functie minus alle x, wat de functie opheft die als deler fungeert, omdat we anders een onbepaaldheid zouden verkrijgen.

$\displaystyle\text{Dom}\left(\frac{f}{g}\right)(x)=\text{Dom}(f)\cap\text{Dom}(g)-\{x:g(x)=0\}$

Als voorbeeld verdelen we de volgende functies:

$f(x)=5^x \qquad g(x)=x-3$

De functieverdeling is als volgt:

$\displaystyle\left(\frac{f}{g}\right)(x)=\frac{f(x)}{g(x)}=\cfrac{5^x}{x-3}$

Aan de andere kant bestaat het domein van elke functie afzonderlijk uit alle reële getallen

$\text{Dom}(f)=\mathbb{R}\qquad\text{Dom}(g)=\mathbb{R}$

Omdat er echter geen nul in de noemer van een breuk kan voorkomen, moeten we in het domein van de resulterende functie alle waarden verwijderen die de noemer opheffen (x=3).

$\displaystyle\text{Dom}\left(\frac{f}{g}\right)(x)=\text{Dom}(f)\cap\text{Dom}(g)-\{x:g(x)=0\}=\mathbb{R}-\{3\}$

Samenstelling van functies

Het samenstellen van functies is de moeilijkste operatie om op te lossen, omdat het het meest gecompliceerde concept is.

Functiesamenstelling bestaat uit de opeenvolgende toepassing van twee functies. Algebraïsch wordt de samenstelling van twee functies als volgt uitgedrukt:

$(g\circ f)(x)=g\Bigl(f(x)\Bigr)$

Aan de andere kant het domein van de samenstelling van functies

$(g\circ f)(x)$

is equivalent aan de verzameling van alle waarden van x in het domein van de functie

$f$

zoals

$f(x)$

behoort tot het domein van de functie

$g.$

$\text{Dom}(g\circ f)=\{x\in\text{Dom}(f)\ | \ f(x)\in \text{Dom}(g)\}$

Gegeven bijvoorbeeld de volgende twee functies:

$f(x)=x^2+1 \qquad g(x)=3x-4$

Om de samengestelde functie te vinden

$f$

gevolgd door

$g$

we moeten de uitdrukking van vervangen

$f(x)$

waar er een is

$x$

in de uitdrukking van

$g(x):$

$\begin{aligned}(g\circ f)(x)&=g\Bigl(f(x)\Bigr)\\[2ex]&= g\Bigl(x^2+1\Bigr)\\[2ex]&=3(x^2+1)-4\\[2ex]&=3x^2+3-4\\[2ex]&=3x^2-1\end{aligned}$

In dit geval bestaat het domein van beide functies volledig uit reële getallen, dus zal het domein van de samengestelde functie ook uit reële getallen bestaan.

$\text{Dom}(g\circ f)=\mathbb{R}$

Zoals u kunt zien, is het samenstellen van functies geen eenvoudige handeling. Daarom raden wij u aan de volgende functiecompositieoefeningen te doen:

➤ Zie: opgeloste oefeningen over de samenstelling van functies

Eigenschappen van bewerkingen met functies

Van alle bewerkingen met functies worden de som en het product gekenmerkt door de volgende eigenschappen:

Associatieve eigenschap : de volgorde waarin 3 of meer functies worden toegevoegd of vermenigvuldigd, is niet relevant.

$f(x)+\bigl[g(x)+h(x)\bigr]=\bigl[f(x)+g(x)\bigr]+h(x)$

$f(x)\cdot \bigl[g(x)\cdot h(x)\bigr]=\bigl[f(x)\cdot g(x)\bigr] \cdot h(x)$

Commutatieve eigenschap : de volgorde van de optelling of vermenigvuldiging van twee functies verandert het resultaat niet.

$f(x)+g(x)=g(x)+f(x)$

$f(x)\cdot g(x)=g(x)\cdot f(x)$

Neutraal element: de sombewerking en de productbewerking hebben constante neutrale elementfuncties
$f(x)=0$

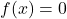
En

$f(x)=1$

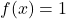
respectievelijk.

Symmetrisch element : de somfunctie heeft de tegenovergestelde functie
$-f(x).$

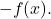
Distributieve eigenschap : deze eigenschap verbindt de som en het product van bewerkingen en is gebaseerd op de volgende gelijkheid:

$f(x)\cdot \bigl[g(x)+h(x)\bigr]=f(x)\cdot g(x)+f(x)\cdot h(x)$