In deze sectie zullen we zien hoe we een stelsel vergelijkingen kunnen bespreken en oplossen volgens de Gauss-Jordan-methode . Dat wil zeggen, bepaal of het een bepaald compatibel systeem (DCS), een onbepaald compatibel systeem (ICS) of een incompatibel systeem is. Daarnaast vindt u voorbeelden en opgeloste oefeningen zodat u de concepten perfect kunt oefenen en verwerken.
Om te begrijpen wat we hierna gaan uitleggen, is het belangrijk dat je al weet hoe je een systeem oplost met behulp van de Gauss-methode . We raden je daarom aan even te kijken voordat je verdergaat.
Compatibele systemen bepaald door de Gauss-methode
Zolang de laatste rij van de Gauss-matrix is
![]()
, zijn
![]()
En
![]()
twee willekeurige getallen, dit is een SCD (Systeem Compatibel Bepaald). Daarom heeft het systeem een unieke oplossing .
De overgrote meerderheid van de systemen is SCD.
Voorbeeld:
We hebben bijvoorbeeld dit systeem:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 3x+2y-z=1 \\[2ex] 3x+8y+z=1\\[2ex] 6x+4y-z=-1 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bab5d5823e45833aa691a3510a2a23eb_l3.png)
Waarvan de uitgebreide matrix is:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 3x+2y-z=1 \\[2ex] 3x+8y+z=1\\[2ex] 6x+4y-z=-1 \end{array} \right\}} \ \longrightarrow \ \left( \begin{array}{ccc|c} 3 & 2 & -1 & 1 \\[2ex] 3 & 8 & 1 & 1 \\[2ex] 6 & 4 & -1 & -1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-1f8daea11edeedfd6b86bb251fe19032_l3.png)
Om het systeem op te lossen moeten we op de rijen van de matrix werken en alle elementen onder de hoofddiagonaal naar 0 converteren. Dus van de tweede rij trekken we de eerste rij af en van de derde rij trekken we de eerste regel af, vermenigvuldigd met 2:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 3 & 2 & -1 & 1 \\[2ex] 3 & 8 & 1 & 1 \\[2ex] 6 & 4 & -1 & -1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -f_1} \\[2ex] \xrightarrow{f_3 -2f_1} & \end{array} \left( \begin{array}{ccc|c} 3 & 2 & -1 & 1 \\[2ex] 0 & 6 & 2 & 0 \\[2ex] 0 & 0 & 1 & -3 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-d68ac25745ddc71d1e7f55f68dd4ea7a_l3.png)
Zodra alle getallen onder de hoofddiagonaal 0 zijn, keren we terug om het systeem in vergelijkingsvorm om te zetten:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 3 & 2 & -1 & 1 \\[2ex] 0 & 6 & 2 & 0 \\[2ex] 0 & 0 & 1 & -3 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 3x+2y-z=1 \\[2ex] 6y+2z=0\\[2ex] 1z=-3 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4457f1b034e72c6945bfe609eff52b9a_l3.png)
Dit systeem is dus SCD , omdat de matrix is verschoven en de laatste rij van het type is
![]()
. Daarom lossen we het op zoals altijd: door de onbekenden van onder naar boven uit de vergelijkingen te elimineren.
![]()
![]()
![]()
Nu we z kennen, vullen we de waarde ervan in de tweede vergelijking in om de waarde van te vinden
![]()
:
![]()
![]()
![]()
![]()
![]()
En ten slotte doen we hetzelfde met de eerste vergelijking: we vervangen de waarden van de andere onbekenden en lossen op
![]()
:
![]()
![]()
![]()
![]()
![]()
![]()
De oplossing van het stelsel vergelijkingen is daarom:
![]()
Incompatibele systemen volgens de methode van Gauss
In de Gauss-matrix hebben we een rij met drie nullen op rij en een getal
![]()
, het is een IS (Incompatibel Systeem) en daarom heeft het systeem geen oplossing .
Voorbeeld:
Stel je bijvoorbeeld voor dat we na het werken met de Gauss-matrix van een systeem het volgende overhouden:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 4 & 1 & -1 & 0 \\[2ex] 0 & 3 & 1 & -1 \\[2ex] 0 & 0 & 0 & 2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-defe65fa616eff800314ebc6dc6f552b_l3.png)
Zoals de laatste regel is
![]()
, dat wil zeggen drie nullen gevolgd door een getal aan het einde, is een IF (Incompatibel systeem) en daarom heeft het systeem geen oplossing .
Hoewel het niet nodig is om het te weten, zul je hieronder zien waarom het geen oplossing heeft.
Als we de laatste regel nemen, krijgen we deze vergelijking:
![]()
Deze vergelijking zal nooit vervuld worden, want welke waarde z ook aanneemt, het vermenigvuldigen met 0 zal nooit 2 opleveren (elk getal vermenigvuldigd met 0 geeft altijd 0). En aangezien aan deze vergelijking nooit zal worden voldaan, heeft het systeem geen oplossing.
Compatibele systemen niet bepaald door de Gauss-methode
Telkens wanneer een rij van de Gauss-matrix gevuld is met 0
![]()
, het is een SCI (Indeterminate Compatible System) en daarom heeft het systeem oneindige oplossingen .
Laten we een voorbeeld bekijken van hoe u een ICS kunt oplossen:
Voorbeeld:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+y+2z=6 \\[2ex] 2x+3y-1z=-2 \\[2ex] 3x+4y+z=4 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-18a63dfebc1f23923714e475aad2e808_l3.png)
Zoals altijd maken we eerst de uitgebreide matrix van het systeem :
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+y+2z=6 \\[2ex] 2x+3y-1z=-2 \\[2ex] 3x+4y+z=4 \end{array} \right\} \ \longrightarrow \ \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 2 & 3 & -1 & -2 \\[2ex] 3 & 4 & 1 & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f273040101827fdfea5c9a4858be5567_l3.png)
Nu willen we dat alle getallen onder de hoofddiagonaal 0 zijn. Dus aan de tweede rij voegen we de eerste rij vermenigvuldigd met -2 toe:
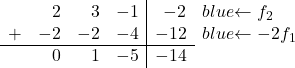
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 2 & 3 & -1 & -2 \\[2ex] 3 & 4 & 1 & 4\end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -2f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 3 & 4 & 1 & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-c889a6f147c6b0430731aa778121af52_l3.png)
Om 3 naar 0 te converteren, voegen we in de derde regel de eerste regel vermenigvuldigd met -3 toe:
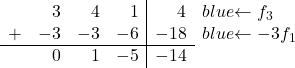
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 3 & 4 & 1 & 4 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 -3f_1} & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 0 & 1 & -5 & -14 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-c5acccc51108267fef6d3320068743aa_l3.png)
Om de 1 in de laatste regel om te zetten naar 0, voegen we in de derde regel de tweede regel vermenigvuldigd met -1 toe:

![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 0 & 1 & -5 & -14 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 -1f_2} & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 0 & 0 & 0 & 0 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-a02e4819adfbe7b80d2952f87f113757_l3.png)
Omdat de laatste regel allemaal 0 is , kunnen we deze verwijderen:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 0 & 0 & 0 & 0 \end{array} \right) \ \longrightarrow \ \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-6aea469dceab08e6aa62571922eb2824_l3.png)
En aangezien we een hele rij gevuld hadden met nullen, is dit een SCI.
We komen dus uit op het volgende systeem:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x+y+2z=6 \\[2ex] y-5z=-14 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-598c031f4cba5a865952a57ed46f0f95_l3.png)
Wanneer het systeem een SCI is, is het noodzakelijk om de waarde van de parameter uit een onbekende te halen
![]()
. En we moeten het systeem oplossen op basis van deze parameter
![]()
.
Daarom kennen we de waarde toe van
![]()
tot z :
![]()
Hoewel we ook een andere onbekende hadden kunnen kiezen om de waarde van te nemen
![]()
.
Nu isoleren we y uit de tweede vergelijking en laten we deze een functie zijn van
![]()
:
![]()
![]()
![]()
En ten slotte verwijderen we x uit de eerste vergelijking en laten we deze ook als functie van staan
![]()
:
![]()
![]()
![]()
![]()
De systeemoplossingen zijn daarom:
![]()
Zoals u kunt zien, laten we, wanneer het systeem SCI is, de oplossingen afhankelijk van de parameter
![]()
. En onthoud dat het oneindige oplossingen heeft, omdat het afhankelijk is van de waarde die het nodig heeft
![]()
, zal de oplossing het een of het ander zijn.
Voordat je verdergaat met de opgeloste oefeningen, moet je weten dat, hoewel we in dit artikel de methode van Gauss gebruiken, de stelling van Rouche een andere manier is om stelsels van lineaire vergelijkingen te bespreken en op te lossen. Sterker nog, het wordt waarschijnlijk meer gebruikt.
Opgeloste oefeningen voor de bespreking van stelsels vergelijkingen met behulp van de Gauss-Jordan methode
Oefening 1
Bepaal om welk type systeem het gaat en los het volgende stelsel vergelijkingen op met behulp van de Gauss-methode:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+y+2z=6 \\[2ex] 2x+3y+5z=8 \\[2ex] 3x+3y+6z=9 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-be4ba1bd1ce7452e66c5189d995d948c_l3.png)
Het eerste dat we moeten doen is de uitgebreide matrix van het systeem:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+y+2z=6 \\[2ex] 2x+3y+5z=8 \\[2ex] 3x+3y+6z=9 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 2 & 3 & 5 & 8 \\[2ex] 3 & 3 & 6 & 9 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-b600f3fc0d79a06eb972dbacb673a780_l3.png)
Nu moeten we alle getallen onder de hoofdarray 0 maken.
We voeren daarom rijbewerkingen uit om de laatste twee termen van de eerste kolom te annuleren:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 2 & 3 & 5 & 8 \\[2ex]3 & 3 & 6 & 9 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 - 2f_1} \\[2ex] \xrightarrow{f_3 - 3f_1}& \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & 1 & -4 \\[2ex] 0 & 0 & 0 & -9 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-a1d832d5bb115666614ae96822c360eb_l3.png)
We hebben een rij van de matrix verkregen die bestaat uit drie nullen gevolgd door een getal. Het is dus een IS (Incompatibel Systeem) en het systeem heeft geen oplossing.
Oefening 2
Bepaal welk type systeem het is en vind de oplossing voor het volgende stelsel vergelijkingen met behulp van de Gauss-methode:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x-2y+3z=1 \\[2ex] -2x+5y-z=5 \\[2ex] -x+3y+2z=6 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7f5aba495f2c6a301e923ee3c6238012_l3.png)
Het eerste dat we moeten doen is de uitgebreide matrix van het systeem:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x-2y+3z=1 \\[2ex] -2x+5y-z=5 \\[2ex] -x+3y+2z=6 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] -2 & 5 & -1 & 5 \\[2ex] -1 & 3 & 2 & 6 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f8bb5e5ab85946bddad72067fe17d937_l3.png)
Nu moeten we alle getallen onder de hoofdarray 0 maken.
We voeren daarom rijbewerkingen uit om de laatste twee termen van de eerste kolom te annuleren:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] -2 & 5 & -1 & 5 \\[2ex] -1 & 3 & 2 & 6 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 + 2f_1} \\[2ex] \xrightarrow{f_3 + f_1} \end{array} \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \\[2ex] 0 & 1 & 5 & 7 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-83e48becaaa6683719ac57eb7d118943_l3.png)
Laten we nu proberen het laatste element uit de tweede kolom te verwijderen:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \\[2ex] 0 & 1 & 5 & 7 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 -f_2} \end{array} \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \\[2ex] 0 & 0 & 0 & 0 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-16a1afc0eb224ee5f05c9e313586854d_l3.png)
Maar we krijgen een hele rij nullen. Dit is dus een SCI en het systeem heeft oneindig veel oplossingen.
Maar omdat het een ICS is, kunnen we het systeem oplossen op basis van
![]()
. We schrappen daarom de 0-regel:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \\[2ex] 0 & 0 & 0 & 0 \end{array} \right) \ \longrightarrow \ \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-5c838c5f1b229d4c8a43ac9ddd8e3629_l3.png)
We drukken de matrix nu uit in de vorm van een stelsel van vergelijkingen met onbekenden:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 1x-2y+3z=1 \\[2ex] 1y+5z=7 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b3fd941d33fec646d16b8181430c9986_l3.png)
Wij geven de waarde van
![]()
Voor
![]()
![]()
Wij vervangen de waarde van
![]()
in de tweede vergelijking om de waarde van te vinden
![]()
![]()
![]()
![]()
En we doen hetzelfde met de eerste vergelijking: we vervangen de waarden van de andere onbekenden en we wissen
![]()
![]()
![]()
![]()
![]()
De oplossing van het stelsel vergelijkingen is daarom:
![]()
Oefening 3
Zoek welk type systeem het is en los het volgende stelsel vergelijkingen op met de Gauss-methode:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 4x-4y+z=-4 \\[2ex] x+3y+z=2 \\[2ex] x+5y+2z=6 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b04370b42854e53c650ca0eae14aadb5_l3.png)
Het eerste dat we moeten doen is de uitgebreide matrix van het systeem:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 4x-4y+z=-4 \\[2ex] x+3y+z=2 \\[2ex] x+5y+2z=6\end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 4 & -4 & 1 & -4 \\[2ex] 1 & 3 & 1 & 2 \\[2ex] 1 & 5 & 2 & 6 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-ff2c7644e19fdf405f3c5c42ffc0ee98_l3.png)
Om de Gauss-methode toe te passen is het eenvoudiger als het eerste getal op de eerste regel een 1 is. We zullen daarom de volgorde van regels 1 en 2 veranderen:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 4 & -4 & 1 & -4 \\[2ex] 1 & 3 & 1 & 2 \\[2ex] 1 & 5 & 2 & 6 \end{array} \right) \begin{array}{c} \xrightarrow{f_1 \rightarrow f_2} \\[2ex] \xrightarrow{f_2 \rightarrow f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} 1 & 3 & 1 & 2 \\[2ex] 4 & -4 & 1 & -4 \\[2ex] 1 & 5 & 2 & 6 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-471d89605d4bf6ddef1896a8fbe4c5ea_l3.png)
Nu moeten we alle getallen onder de hoofdarray 0 maken.
We voeren daarom rijbewerkingen uit om de laatste twee termen van de eerste kolom te annuleren:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 3 & 1 & 2 \\[2ex] 4 & -4 & 1 & -4 \\[2ex] 1 & 5 & 2 & 6 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 - 4f_1} \\[2ex] \xrightarrow{f_3 -f_1} \end{array} \left( \begin{array}{ccc|c} 1 & 3 & 1 & 2 \\[2ex] 0 & -16 & -3 & -12 \\[2ex] 0 & 2 & 1 & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f4d5cbc50b87927077018175c4678e90_l3.png)
Nu converteren we het laatste element van de tweede kolom naar nul:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & 3 & 1 & 2 \\[2ex] 0 & -16 & -3 & -12 \\[2ex] 0 & 2 & 1 & 4 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{8f_3 + f_2} \end{array} \left( \begin{array}{ccc|c}1 & 3 & 1 & 2 \\[2ex] 0 & -16 & -3 & -12 \\[2ex] 0 & 0 & 5 & 20 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-9013720883fd719e2bd0779bfbaa7a9f_l3.png)
Dit systeem is SCD , omdat het ons is gelukt de matrix te verschuiven en de laatste rij van het type is
![]()
. Daarom zal het een unieke oplossing hebben.
Zodra alle getallen onder de hoofddiagonaal 0 zijn, kunnen we nu het stelsel vergelijkingen oplossen. Om dit te doen, drukken we de matrix opnieuw uit in de vorm van een stelsel van vergelijkingen met onbekenden:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 3 & 1 & 2 \\[2ex] 0 & -16 & -3 & -12 \\[2ex] 0 & 0 & 5 & 20 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x+3y+1z=2 \\[2ex] -16y-3z=-12 \\[2ex] 5z=20 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0f0433738d5d0a22bdd3b04dbd44fd1e_l3.png)
En we lossen de onbekenden van de vergelijkingen van onder naar boven op. We lossen eerst de laatste vergelijking op:
![]()
![]()
Nu vervangen we de waarde van z in de tweede vergelijking om de waarde van y te vinden:
![]()
![]()
![]()
![]()
![]()
En we doen hetzelfde met de eerste vergelijking: we vervangen de waarden van de andere onbekenden en we lossen op voor x:
![]()
![]()
![]()
![]()
De oplossing van het stelsel vergelijkingen is daarom:
![]()
Oefening 4
Bepaal welk type systeem het is en los het volgende stelsel vergelijkingen op met de Gauss-methode:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x-y+4z=2 \\[2ex] -3x-3y+3z=7 \\[2ex] -2x-4y+7z=9 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4e8a133547b4719d7833a792550fd322_l3.png)
Het eerste dat we moeten doen is de uitgebreide matrix van het systeem:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x-y+4z=2 \\[2ex] -3x-3y+3z=7 \\[2ex] -2x-4y+7z=9 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c}1 & -1 & 4 & 2 \\[2ex] -3 & -3 & 3 & 7 \\[2ex] -2 & -4 & 7 & 9\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-cc41f78456a922a0fbff419d336b0b46_l3.png)
Nu moeten we alle getallen onder de hoofdarray 0 maken.
We voeren daarom rijbewerkingen uit om de laatste twee termen van de eerste kolom te annuleren:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] -3 & -3 & 3 & 7 \\[2ex] -2 & -4 & 7 & 9\end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 + 3f_1} \\[2ex] \xrightarrow{f_3 + 2f_1} \end{array} \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13\\[2ex] 0 & -6 & 15 & 13\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-ff92912f653c6aca7ceb7c990c9635a3_l3.png)
Laten we nu proberen het laatste element uit de tweede kolom te verwijderen:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13\\[2ex] 0 & -6 & 15 & 13\end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 -1f_2} \end{array} \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13\\[2ex] 0 & 0 & 0 & 0 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-3c6904a64a721f3a92bef8c6b7d713cf_l3.png)
Maar we krijgen een hele rij nullen. Dit is dus een SCI en het systeem heeft oneindig veel oplossingen.
Maar omdat het een ICS is, kunnen we het systeem oplossen op basis van
![]()
. We schrappen daarom de 0-regel:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13\\[2ex] 0 & 0 & 0 & 0 \end{array} \right) \ \longrightarrow \ \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-6d856e2c1246f3629d68a7bcd3cd759a_l3.png)
We drukken de matrix nu uit in de vorm van een stelsel van vergelijkingen met onbekenden:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 1x-1y+4z=2 \\[2ex] -6y+15z=13 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a4cf1265bfc12f94580de183230c8b7c_l3.png)
Wij geven de waarde van
![]()
Voor
![]()
![]()
Wij vervangen de waarde van
![]()
in de tweede vergelijking om de waarde van te vinden
![]()
![]()
![]()
![]()
![]()
En we doen hetzelfde met de eerste vergelijking: we vervangen de waarden van de andere onbekenden en we wissen
![]()
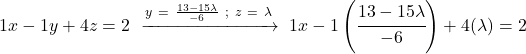
![]()
![]()
We hebben een som met breuken. Daarom herleiden we alle termen tot een gemeenschappelijke noemer:
![]()
![]()
Omdat ze nu allemaal dezelfde noemer hebben, kunnen we ze in één breuk groeperen:
![]()
En tenslotte werken we met de teller:
![]()
![]()
De oplossing van het stelsel vergelijkingen is daarom:
![]()