Bespreking van stelsels van vergelijkingen met parameters -

Op deze pagina zullen we zien hoe we een stelsel vergelijkingen met parameters kunnen bespreken en oplossen. Daarnaast vind je voorbeelden en opgeloste oefeningen van stelsels lineaire vergelijkingen om te oefenen.

Aan de andere kant is het voor het analyseren van stelsels van lineaire vergelijkingen belangrijk dat je weet wat de regel van Cramer is en wat de stelling van Rouché-Frobenius is , omdat we ze voortdurend zullen gebruiken.

Voorbeeld van een systeem van lineaire vergelijkingen met parameters

Bespreek en los het volgende stelsel vergelijkingen op in termen van de parameter m :

$\begin{cases} x+y+2z= 2 \\[1.5ex] -x+my+2z=0 \\[1.5ex] 3x+mz = 4\end{cases}$

We maken eerst de matrix A en de uitgebreide matrix A’ van het systeem:

$\displaystyle A= \left( \begin{array}{ccc}1 & 1 & 2 \\[1.1ex] -1 & m & 2 \\[1.1ex] 3 & 0 & m \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 1 & 2 & 2 \\[1.1ex] -1 & m & 2 & 0 \\[1.1ex] 3 & 0 & m & 4 \end{array} \right)$

Nu lossen we de determinant van A op met behulp van de regel van Sarrus, om te zien welke rangorde de matrix heeft:

$\displaystyle\begin{aligned} \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 1 & 2 \\[1.1ex] -1 & m & 2 \\[1.1ex] 3 & 0 & m \end{vmatrix} & =m^2+6+0-6m-0+m \\ & = m^2-5m+6 \end{aligned}$

Het resultaat van de determinant van A hangt dus af van de waarde van m . We zullen dus kijken voor welke waarden van m de determinant verdwijnt. Om dit te doen, stellen we het resultaat gelijk aan 0 :

$\displaystyle m^2-5m+6 = 0$

En we lossen de kwadratische vergelijking op met de formule:

$\displaystyle m = \cfrac{-b \pm \sqrt{b^2-4ac}}{2a}$

$\displaystyle m = \cfrac{-(-5) \pm \sqrt{(-5)^2-4\cdot 1 \cdot 6}}{2 \cdot 1} = \cfrac{5 \pm \sqrt{25-24}}{2} =\cfrac{5 \pm 1}{2} = \begin{cases} \bm{m = 3} \\[2ex] \bm{m =2} \end{cases}$

Dus als m gelijk is aan 2 of 3, zal de determinant van A 0 zijn. En als m verschillend is van 2 en verschillend van 3, zal de determinant van A verschillend zijn van 0.

We moeten daarom elk geval afzonderlijk analyseren:

m≠3 en m≠2:

Zoals we zojuist hebben gezien, is de determinant van de matrix A verschillend van 0 als de parameter m verschillend is van 2 en 3. Daarom is de rangorde van A 3 .

$\displaystyle rg(A)=3$

Bovendien is de rangorde van matrix A’ ook 3 , omdat daarbinnen een 3×3-submatrix zit waarvan de determinant anders is dan 0. En deze kan niet de rangorde 4 hebben omdat ‘we geen 4×4-determinant kunnen maken.

$\displaystyle rg(A')=3$

Omdat de rangorde van matrix A gelijk is aan de rangorde van matrix A’ en aan het aantal onbekenden van het systeem (3), weten we volgens de stelling van Rouché-Frobenius dat het een Bepaald Systeem Compatibel (SCD) is. :

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}$

Zodra we weten dat het systeem een Compatible Bepaald Systeem (DCS) is, passen we de regel van Cramer toe om het op te lossen. Om dit te doen, bedenk dat de matrix A, zijn determinant en de matrix A’ zijn:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 1 & 2 \\[1.1ex] -1 & m & 2 \\[1.1ex] 3 & 0 & m \end{vmatrix} = m^2-5m+6$

Om x te berekenen met de regel van Cramer, veranderen we de eerste kolom van de determinant van matrix A in de kolom met onafhankelijke termen en delen we deze door de determinant van A:

$\displaystyle\bm{x} = \cfrac{\begin{vmatrix} 2 & 1 & 2\\[1.1ex]0&m&2 \\[1.1ex] 4 & 0 & m \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{2m^2+8-8m}{m^2-5m+6}$

Om y te berekenen met de regel van Cramer, veranderen we de tweede kolom van de determinant van A in de kolom met onafhankelijke termen en delen we deze door de determinant van A:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix}1 & 2 & 2 \\[1.1ex] -1 & 0 & 2 \\[1.1ex] 3 & 4 & m \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}}=\cfrac{-4+2m}{m^2-5m+6}$

Om z te berekenen met de regel van Cramer, veranderen we de derde kolom van de determinant van A in de kolom met onafhankelijke termen en delen we deze door de determinant van A:

$\displaystyle \bm{z} = \cfrac{\begin{vmatrix} 1 & 1 & 2 \\[1.1ex] -1 & m & 0 \\[1.1ex] 3 & 0 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-2m+4}{m^2-5m+6}$

Daarom is de oplossing van het stelsel vergelijkingen voor het geval m≠3 en m≠2:

$\displaystyle \bm{x =} \cfrac{\bm{2m^2+8-8m}}{\bm{m^2-5m+6}} \qquad \bm{y=} \cfrac{\bm{-4+2m}}{\bm{m^2-5m+6}} \qquad \bm{z =} \cfrac{\bm{-2m+4}}{\bm{m^2-5m+6}}$

Zoals je kunt zien, is in dit geval de oplossing van het stelsel vergelijkingen een functie van m.

Zodra we de oplossing hebben gevonden voor wanneer m verschillend is van 2 en 3, zullen we het systeem oplossen voor wanneer m gelijk is aan 2:

m=2:

We zullen nu het systeem analyseren als de parameter m gelijk is aan 2. In dit geval zijn de matrices A en A’:

$\displaystyle A= \left( \begin{array}{ccc}1 & 1 & 2 \\[1.1ex] -1 & 2 & 2 \\[1.1ex] 3 & 0 & 2 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 1 & 2 & 2 \\[1.1ex] -1 & 2 & 2 & 0 \\[1.1ex] 3 & 0 & 2 & 4 \end{array} \right)$

Zoals we eerder zagen, is de determinant van A, wanneer m=2, 0. Daarom heeft matrix A niet rang 3. Maar binnenin heeft hij 2×2 determinanten die verschillen van 0, bijvoorbeeld:

$\displaystyle \begin{vmatrix}1 & 1 \\[1.1ex] -1 & 2 \end{vmatrix} = 2 - (-1)=3 \neq 0$

In dit geval is de rangorde van A dus 2 :

$\displaystyle rg(A)=2$

Zodra we de rangorde van matrix A kennen, berekenen we de rangorde van A’. De determinant van de eerste 3 kolommen geeft 0, dus we proberen de andere mogelijke 3×3 determinanten in de matrix A’:

$\displaystyle \begin{vmatrix} 1 & 2 & 2 \\[1.1ex] 2 & 2 & 0 \\[1.1ex] 0 & 2 & 4 \end{vmatrix} = 0 \qquad \begin{vmatrix} 1 & 2 & 2 \\[1.1ex] -1 & 2 & 0 \\[1.1ex] 3 & 2 & 4 \end{vmatrix}=0\qquad \begin{vmatrix} 1 & 1 & 2 \\[1.1ex] -1 & 2 & 0 \\[1.1ex] 3 & 0 & 4\end{vmatrix}=0$

Alle mogelijke determinanten van dimensie 3×3 geven 0. Maar uiteraard heeft matrix A’ dezelfde 2×2 niet-0 determinant als matrix A:

$\displaystyle \begin{vmatrix}1 & 1 \\[1.1ex] -1 & 2 \end{vmatrix} = 2 - (-1)=3 \neq 0$

Daarom heeft de matrix A’ ook rang 2 :

$\displaystyle rg(A')=2$

Dus aangezien de rangorde van matrix A gelijk is aan de rangorde van matrix A’, maar deze twee kleiner zijn dan het aantal onbekenden van systeem (3), weten we door de stelling van Rouché-Frobenius dat dit een onbepaald compatibel systeem is. (ICS):

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}$

Omdat het een ICS is, moeten we het systeem transformeren om het op te lossen. Om dit te doen, moeten we eerst een vergelijking uit het systeem verwijderen. In dit geval verwijderen we de laatste vergelijking:

$\begin{cases} x+y+2z= 2 \\[1.5ex] -x+2y+2z=0 \\[1.5ex] \cancel{3x+2z = 4} \end{cases} \longrightarrow \quad \begin{cases} x+y+2z= 2 \\[1.5ex] -x+2y+2z=0\end{cases}$

Laten we nu de variabele z naar λ converteren:

$\begin{cases}x+y+2z= 2 \\[1.5ex] -x+2y+2z=0 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} x+y+2\lambda= 2 \\[1.5ex] -x+2y+2\lambda=0\end{cases}$

En we plaatsen de termen met λ bij de onafhankelijke termen:

$\begin{cases}x+y=2-2\lambda \\[1.5ex] -x+2y=-2\lambda \end{cases}$

Daarom blijven de matrix A en de matrix A’ van het systeem:

$\displaystyle A= \left( \begin{array}{ccc} 1 & 1 \\[1.1ex] -1 & 2 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 1 & 1 & 2 -2\lambda \\[1.1ex] -1 & 2 & -2\lambda \end{array} \right)$

Ten slotte passen we, zodra we het systeem hebben getransformeerd, de regel van Cramer toe . Om dit te doen, lossen we eerst de determinant van A op:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 1 \\[1.1ex] -1 & 2\end{vmatrix} =2-(-1)=3$

Om x te berekenen met de regel van Cramer, veranderen we de eerste kolom van de determinant van A in de kolom met onafhankelijke termen en delen we deze door de determinant van A:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 2 -2\lambda & 1 \\[1.1ex] -2\lambda & 2 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{4-4\lambda-(-2\lambda)}{3} = \cfrac{\bm{4-2\lambda}}{\bm{3}}$

Om y te berekenen met de regel van Cramer, veranderen we de tweede kolom van de determinant van A in de kolom met onafhankelijke termen en delen we deze door de determinant van A:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} 1 & 2 -2\lambda \\[1.1ex] -1 & -2\lambda \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}}=\cfrac{-2\lambda -(-2+2\lambda)}{3} = \cfrac{\bm{2-4\lambda} }{\bm{3}}$

Zodat wanneer m=2 de oplossing van het stelsel vergelijkingen een functie is van λ, aangezien het een SCI is en daarom oneindige oplossingen heeft:

$\displaystyle \bm{x =} \cfrac{\bm{4-2\lambda}}{\bm{3}} \qquad \bm{y=}\cfrac{\bm{2-4\lambda}}{\bm{3}} \qquad \bm{z=\lambda}$

We hebben de oplossing van het systeem al geanalyseerd wanneer de parameter m verschillend is van 2 en 3, en wanneer deze gelijk is aan 2. We hebben daarom alleen het laatste geval nodig: wanneer m de waarde 3 aanneemt:

m=3:

We zullen nu analyseren wat er gebeurt als de parameter m 3 is. In dit geval zijn de matrices A en A’:

$\displaystyle A= \left( \begin{array}{ccc}1 & 1 & 2 \\[1.1ex] -1 & 3 & 2 \\[1.1ex] 3 & 0 & 3 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 1 & 2 & 2 \\[1.1ex] -1 & 3 & 2 & 0 \\[1.1ex] 3 & 0 & 3 & 4 \end{array} \right)$

Zoals we eerder zagen, is de determinant van A, wanneer m=3, 0. De matrix A heeft dus niet rang 3. Maar daarin zitten 2×2 determinanten die verschillen van 0, bijvoorbeeld:

$\displaystyle \begin{vmatrix}1 & 1 \\[1.1ex] -1 & 3 \end{vmatrix} = 3 - (-1)=4 \neq 0$

In dit geval is de rangorde van A dus 2 :

$\displaystyle rg(A)=2$

Zodra we de rangorde van matrix A kennen, berekenen we de rangorde van A’. De determinant van de eerste 3 kolommen geeft 0, we proberen daarom een andere 3×3 determinant die zich binnen de matrix A’ bevindt, bijvoorbeeld die van de laatste 3 kolommen:

$\displaystyle \begin{vmatrix} 1 & 2 & 2 \\[1.1ex] 3 & 2 & 0 \\[1.1ex] 0 & 3 & 4\end{vmatrix}=2$

Aan de andere kant bevat matrix A’ wel een determinant waarvan het resultaat anders is dan 0, daarom heeft matrix A’ rang 3 :

$\displaystyle rg(A')=3$

Wanneer m = 3 is de rangorde van matrix A dus lager dan de rangorde van matrix A’. Uit de stelling van Rouché-Frobenius leiden we dus af dat het systeem een incompatibel systeem (IS) is :

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas}=3\end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A)=2 \ \neq \ rg(A') = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SI}\phantom{^9_9}} \end{array}$

Daarom heeft het stelsel vergelijkingen geen oplossing als m = 3.

Samenvatting van het voorbeeld:

Zoals we hebben gezien hangt de oplossing van het stelsel vergelijkingen af van de waarde van de parameter m . Hier is een samenvatting van alle mogelijke gevallen:

m≠3 en m≠2:

$\displaystyle \bm{SCD} \longrightarrow \begin{cases} x = \cfrac{2m^2+8-8m}{m^2-5m+6} \\[3.5ex] y =\cfrac{-4+2m}{m^2-5m+6} \\[3.5ex] z = \cfrac{-2m+4}{m^2-5m+6} \end{cases}$

m=2:

$\displaystyle \bm{SCI} \longrightarrow \begin{cases} x = \cfrac{4-2\lambda}{3} \\[3.5ex] y= \cfrac{2-4\lambda}{3} \\[3.5ex] z = \lambda \end{cases}$

m=3:

$\displaystyle \bm{SI} \longrightarrow$

Het systeem heeft geen oplossing.

Hier hebben we het hele proces gedaan met behulp van de stelling van Rouche en de regel van Cramer, maar stelsels van vergelijkingen met parameters kunnen ook worden besproken en opgelost met de methode van Gauss (met oefeningen) . U kunt meer over deze methode te weten komen op de gelinkte pagina, waar u stap voor stap een gedetailleerde uitleg van de procedure vindt, evenals voorbeelden en opgeloste oefeningen.

Opgeloste discussieproblemen van stelsels van lineaire vergelijkingen met parameters

Oefening 1

Bespreek en los het volgende stelsel van parameterafhankelijke lineaire vergelijkingen op:

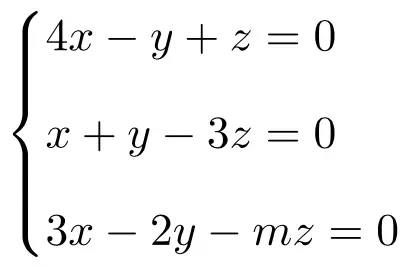
opgeloste oefening van stelsels van vergelijkingen met parameters

zie oplossing

We maken eerst de matrix A en de uitgebreide matrix A’ van het systeem:

$\displaystyle A= \left( \begin{array}{ccc} 4 & -1 & 1 \\[1.1ex] 1 & 1 & -3 \\[1.1ex] 3 & -2 & -m \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}4 & -1 & 1 & 0 \\[1.1ex] 1 & 1 & -3 & 0 \\[1.1ex] 3 & -2 & -m & 0\end{array} \right)$

We moeten nu de rangorde van matrix A vinden. Om dit te doen, controleren we of de determinant van de gehele matrix anders is dan 0:

$\displaystyle \begin{aligned}\begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 4 & -1 & 1 \\[1.1ex] 1 & 1 & -3 \\[1.1ex] 3 & -2 & -m \end{vmatrix} & =-4m+9-2-3-24-m \\ & =-5m-20 \end{aligned}$

Het resultaat van de determinant van A hangt af van de waarde van m. We zullen dus kijken voor welke waarden van m de determinant verdwijnt. Om dit te doen, stellen we het resulterende resultaat gelijk aan 0 en lossen we de vergelijking op:

$-5m-20 = 0$

$-5m = 20$

$m = \cfrac{20}{-5} = -4$

Dus als m -4 is, zal de determinant van A 0 zijn. En als m anders is dan -4, zal de determinant van A anders zijn dan 0. We moeten daarom elk geval afzonderlijk analyseren:

m≠-4:

Zoals we zojuist hebben gezien, is de determinant van matrix A anders dan 0 als de parameter m anders is dan -4. Daarom is de rangorde van A 3.

$\displaystyle rg(A)=3$

Bovendien is de rangorde van matrix A’ ook 3, omdat daarbinnen een 3×3-submatrix zit waarvan de determinant verschilt van 0. En deze kan niet de rangorde 4 hebben, aangezien ‘we geen 4×4-determinant kunnen maken.

$\displaystyle rg(A')=3$

Door de stelling van Rouché-Frobenius toe te passen, weten we daarom dat dit een compatibel bepaald systeem (SCD) is, omdat het bereik van A gelijk is aan het bereik van A’ en het aantal onbekenden.

Zodra we weten dat het systeem een SCD is, passen we de regel van Cramer toe om het op te lossen. Om dit te doen, bedenk dat de matrix A, zijn determinant en de matrix A’ zijn:

$\displaystyle A= \left( \begin{array}{ccc} 4 & -1 & 1 \\[1.1ex] 1 & 1 & -3 \\[1.1ex] 3 & -2 & -m \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 4 & -1 & 1 & 0 \\[1.1ex] 1 & 1 & -3 & 0 \\[1.1ex] 3 & -2 & -m & 0\end{array} \right)$

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 4 & -1 & 1 \\[1.1ex] 1 & 1 & -3 \\[1.1ex] 3 & -2 & -m\end{vmatrix} =-5m-20$

Om xatex] te berekenen met de regel van Cramer, veranderen we de eerste kolom van de determinant van A door de kolom met onafhankelijke termen en delen we deze door de determinant van A:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 0 & -1 & 1 \\[1.1ex] 0 & 1 & -3 \\[1.1ex] 0 & -2 & -m\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{0}{-5m-20} = \bm{0}$

Om het onbekende te berekenen, veranderen we met de regel van Cramer de tweede kolom van de determinant van A door de kolom met onafhankelijke termen en delen we deze door de determinant van A:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} 4 & 0 & 1 \\[1.1ex] 1 & 0 & -3 \\[1.1ex] 3 & 0 & -m \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{0}{-5m-20} = \bm{0}$

Om z te berekenen met de regel van Cramer, veranderen we de derde kolom van de determinant van A in de kolom met onafhankelijke termen en delen we deze door de determinant van A:

$\displaystyle \bm{z} = \cfrac{\begin{vmatrix}4 & -1 & 0 \\[1.1ex] 1 & 1 & 0 \\[1.1ex] 3 & -2 & 0 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{0}{-5m-20} = \bm{0}$

Daarom is de oplossing van het stelsel vergelijkingen voor het geval m≠-4:

x=0 y=0 z=0

m=-4:

We zullen nu het systeem analyseren als de parameter m -4 is. In dit geval zijn de matrices A en A’:

$\displaystyle A= \left( \begin{array}{ccc} 4 & -1 & 1 \\[1.1ex] 1 & 1 & -3 \\[1.1ex] 3 & -2 & 4 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}4 & -1 & 1 & 0 \\[1.1ex] 1 & 1 & -3 & 0 \\[1.1ex] 3 & -2 & 4 & 0\end{array} \right)$

Zoals we eerder zagen, is de determinant van A, wanneer m=-4, 0. De matrix A heeft dus niet de rangorde 3. Maar daarbinnen heeft hij 2×2 determinanten die verschillen van 0, bijvoorbeeld:

$\displaystyle \begin{vmatrix}4 & -1 \\[1.1ex] 1 & 1 \end{vmatrix} =4-(-1)=5 \neq 0$

Omdat de matrix een determinant van orde 2 heeft die verschilt van 0, heeft matrix A rang 2:

$\displaystyle rg(A)=2$

Zodra we de rang van A kennen, berekenen we de rang van A’. We weten al dat de determinant van de eerste 3 kolommen 0 oplevert, dus proberen we de andere mogelijke 3×3 determinanten:

$\displaystyle \begin{vmatrix} -1 & 1 & 0 \\[1.1ex] 1 & -3 & 0 \\[1.1ex] -2 & 4 & 0 \end{vmatrix} = 0 \quad \begin{vmatrix}4 & 1 & 0 \\[1.1ex] 1 & -3 & 0 \\[1.1ex] 3 & 4 & 0 \end{vmatrix} = 0 \quad \begin{vmatrix}4 & -1 & 0 \\[1.1ex] 1 & 1 & 0 \\[1.1ex] 3 & -2 & 0\end{vmatrix} = 0$

Alle 3×3 determinanten van matrix A’ zijn 0, dus matrix A’ zal ook niet van rang 3 zijn. Binnenin heeft het echter determinanten van orde 2 die verschillen van 0. Bijvoorbeeld:

$\displaystyle \begin{vmatrix}4 & -1 \\[1.1ex] 1 & 1 \end{vmatrix} =4-(-1)=5 \neq 0$

Dus de matrix A’ zal van rang 2 zijn:

$\displaystyle rg(A')=2$

De omvang van matrix A is gelijk aan de omvang van matrix A’, maar deze twee zijn kleiner dan het aantal onbekenden in systeem (3), daarom is c volgens de stelling van Rouché-Frobenius een onbepaald compatibel systeem (ICS):

Het is een ICS-systeem, dus we moeten het systeem transformeren om het op te lossen. We elimineren eerst één vergelijking, die in dit geval de laatste zal zijn:

$\begin{cases} 4x-y+z= 0 \\[1.5ex] x+y-3z=0 \\[1.5ex] \cancel{3x-2y+4z = 0} \end{cases} \longrightarrow \quad \begin{cases} 4x-y+z= 0 \\[1.5ex] x+y-3z=0\end{cases}$

Laten we nu de variabele z naar λ converteren:

$\begin{cases}4x-y+z= 0 \\[1.5ex] x+y-3z=0 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} 4x-y+\lambda= 0 \\[1.5ex] x+y-3\lambda=0\end{cases}$

En we plaatsen de termen met λ bij de onafhankelijke termen:

$\begin{cases} 4x-y=-\lambda \\[1.5ex] x+y=3\lambda \end{cases}$

Zodanig dat de matrix A en de matrix A’ van het systeem blijven:

$\displaystyle A= \left( \begin{array}{ccc} 4 & -1 \\[1.1ex] 1 & 1 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 4 & -1 & -\lambda \\[1.1ex] 1 & 1 & 3\lambda \end{array} \right)$

Als we tenslotte het systeem hebben getransformeerd, passen we de regel van Cramer toe. Om dit te doen, lossen we eerst de determinant van A op:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 4 & -1 \\[1.1ex] 1 & 1 \end{vmatrix} = 4-(-1)=5$

Om x te berekenen met de regel van Cramer, veranderen we de eerste kolom van de determinant van A in de kolom met onafhankelijke termen en delen we deze door de determinant van A:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix}-\lambda & -1 \\[1.1ex] 3\lambda & 1 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-\lambda-(-3\lambda)}{5} =\cfrac{\bm{2\lambda}}{\bm{5}}$

Om het onbekende te berekenen, veranderen we met de regel van Cramer de tweede kolom van de determinant van A door de kolom met onafhankelijke termen en delen we deze door de determinant van A:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} 4 & -\lambda \\[1.1ex] 1 & 3\lambda \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{12\lambda-(-\lambda)}{5}=\cfrac{\bm{13\lambda}}{\bm{5}}$

Zodat wanneer m=-4 de oplossing van het stelsel vergelijkingen een functie is van λ, aangezien het een SCI is en daarom oneindige oplossingen heeft:

$\displaystyle \bm{x =}\cfrac{\bm{2\lambda}}{\bm{5}}\qquad \bm{y=}\cfrac{\bm{13\lambda}}{\bm{5}} \qquad \bm{z=\lambda}$

Oefening 2

Bespreek en vind de oplossing voor het volgende systeem van parameterafhankelijke lineaire vergelijkingen:

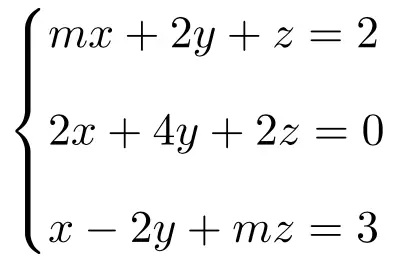
oefening opgelost stap voor stap systeem van lineaire vergelijkingen met parameters

zie oplossing

Het eerste wat je moet doen is de matrix A en de uitgebreide matrix A’ van het systeem:

$\displaystyle A= \left( \begin{array}{ccc} m & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & m\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}m & 2 & 1 & 2 \\[1.1ex] 2 & 4 & 2 & 0 \\[1.1ex] 1 & -2 & m & 3\end{array} \right)$

We moeten nu de rangorde van matrix A vinden. Om dit te doen, controleren we of de determinant van de gehele matrix anders is dan 0:

$\displaystyle \begin{aligned}\begin{vmatrix}A \end{vmatrix}= \begin{vmatrix}m & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & m\end{vmatrix} & =4m^2+4-4-4+4m-4m \\ & =4m^2-4 \end{aligned}$

$4m^2-4 = 0$

$4m^2=4$

$m^2 = \cfrac{4}{4}$

$m^2 = 1$

$m = \pm 1$

Dus als m +1 of -1 is, zal de determinant van A 0 zijn. En als m verschillend is van +1 en -1, zal de determinant van A anders zijn dan 0. We moeten daarom elk geval analyseren door:

m≠+1 en m≠-1:

Zoals we zojuist hebben gezien, is de determinant van matrix A verschillend van 0 als de parameter m verschillend is van +1 en -1. Daarom is de rangorde van A 3.

$\displaystyle rg(A)=3$

$\displaystyle rg(A')=3$

Zodra we weten dat het systeem een SCD is, passen we de regel van Cramer toe om het op te lossen. Om dit te doen, bedenk dat de matrix A, zijn determinant en de matrix A’ zijn:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix}m & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & m\end{vmatrix}=4m^2-4$

Om x te berekenen met de regel van Cramer, veranderen we de eerste kolom van de determinant van A in de kolom met onafhankelijke termen en delen we deze door de determinant van A:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 2& 2 & 1 \\[1.1ex] 0 & 4 & 2 \\[1.1ex] 3 & -2 & m\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{\bm{8m+8}}{\bm{4m^2-4}}$

Om het onbekende te berekenen, veranderen we met de regel van Cramer de tweede kolom van de determinant van A door de kolom met onafhankelijke termen en delen we deze door de determinant van A:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} m & 2 & 1 \\[1.1ex] 2 & 0 & 2 \\[1.1ex] 1 & 3 & m\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{\bm{-10m+10}}{\bm{4m^2-4}}$

Om z te berekenen met de regel van Cramer, veranderen we de derde kolom van de determinant van A in de kolom met onafhankelijke termen en delen we deze door de determinant van A:

$\displaystyle \bm{z} = \cfrac{\begin{vmatrix}m & 2 & 2 \\[1.1ex] 2 & 4 & 0 \\[1.1ex] 1 & -2 & 3 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{\bm{12m-28}}{\bm{4m^2-4}}$

Daarom is de oplossing van het stelsel vergelijkingen voor het geval m≠+1 en m≠-1:

$\displaystyle \bm{x = }\cfrac{\bm{8m+8}}{\bm{4m^2-4}} \qquad \bm{y=}\cfrac{\bm{-10m+10}}{\bm{4m^2-4}}\qquad \bm{z =} \cfrac{\bm{12m-28}}{\bm{4m^2-4}}$

m=+1:

We zullen nu het systeem analyseren als de parameter m gelijk is aan 1. In dit geval zijn de matrices A en A’:

$\displaystyle A= \left( \begin{array}{ccc} 1 & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & 1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}1 & 2 & 1 & 2 \\[1.1ex] 2 & 4 & 2 & 0 \\[1.1ex] 1 & -2 & 1 & 3\end{array} \right)$

Zoals we eerder zagen, is de determinant van A, wanneer m=+1, 0. De matrix A heeft dus niet rang 3. Maar daarbinnen heeft hij 2×2 determinanten die verschillen van 0, bijvoorbeeld:

$\displaystyle \begin{vmatrix}2 & 4\\[1.1ex] 1 & -2 \end{vmatrix} =-4-4=-8 \neq 0$

Omdat de matrix een determinant van orde 2 heeft die verschilt van 0, heeft matrix A rang 2:

$\displaystyle rg(A)=2$

Zodra we de rang van A kennen, berekenen we de rang van A’. We weten al dat de determinant van de eerste 3 kolommen 0 oplevert, dus nu proberen we bijvoorbeeld met de determinant van de laatste 3 kolommen:

$\displaystyle \begin{vmatrix} 2 & 1 & 2 \\[1.1ex] 4 & 2 & 0 \\[1.1ex] -2 & 1 & 3 \end{vmatrix} = 16$

Aan de andere kant bevat matrix A’ wel een 3×3 determinant waarvan het resultaat anders is dan 0, zodat matrix A’ van rang 3 is:

$\displaystyle rg(A')=3$

Dus als m=+1 is de rangorde van matrix A kleiner dan de rangorde van matrix A’. Uit de stelling van Rouché-Frobenius leiden we dus af dat het systeem een incompatibel systeem (IS) is:

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = 2 \ \neq \ rg(A') = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SI}\phantom{^9_9}} \end{array}$

Daarom heeft het stelsel vergelijkingen geen oplossing als m=+1 , aangezien het een incompatibel systeem is.

m=-1:

We zullen nu het systeem analyseren als de parameter m -1 is. In dit geval zijn de matrices A en A’:

$\displaystyle A= \left( \begin{array}{ccc} -1 & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & -1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}-1 & 2 & 1 & 2 \\[1.1ex] 2 & 4 & 2 & 0 \\[1.1ex] 1 & -2 & -1 & 3\end{array} \right)$

Zoals we eerder zagen, is de determinant van A, wanneer m=-1, 0. De matrix A heeft dus niet rang 3. Maar daarbinnen heeft hij 2×2 determinanten die verschillen van 0, bijvoorbeeld:

$\displaystyle \begin{vmatrix}-1 & 2\\[1.1ex] 2 & 4 \end{vmatrix} =-4-4=-8 \neq 0$

Omdat de matrix een determinant van orde 2 heeft die verschilt van 0, heeft matrix A rang 2:

$\displaystyle rg(A)=2$

Zodra we de rang van A kennen, berekenen we de rang van A’. We weten al dat de determinant van de eerste 3 kolommen 0 oplevert, dus proberen we nu bijvoorbeeld met de determinant van de kolommen 1, 3 en 4:

$\displaystyle \begin{vmatrix} -1 & 1 & 2 \\[1.1ex] 2 & 2 & 0 \\[1.1ex] 1 & -1 & 3\end{vmatrix} = -20$

Aan de andere kant bevat matrix A’ wel een 3×3 determinant waarvan het resultaat anders is dan 0, zodat matrix A’ van rang 3 is:

$\displaystyle rg(A')=3$

Wanneer m = -1 is de rangorde van matrix A dus lager dan de rangorde van matrix A’. Uit de stelling van Rouché-Frobenius leiden we dus af dat het systeem een incompatibel systeem (IS) is:

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = 2 \ \neq \ rg(A') = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SI}\phantom{^9_9}} \end{array}$

Daarom heeft het stelsel vergelijkingen geen oplossing als m=-1 , aangezien het een incompatibel systeem is.

Voorbeeld van een systeem van lineaire vergelijkingen met parameters

Samenvatting van het voorbeeld:

Opgeloste discussieproblemen van stelsels van lineaire vergelijkingen met parameters

Oefening 1

Oefening 2

Laat een reactie achter Reactie annuleren