Bereken het kleinste gemene veelvoud (lcm)

Het kleinste gemene veelvoud (LCM) van twee of meer getallen is het kleinste (niet-nul) veelvoud dat deze getallen gemeen hebben. Het is de omgekeerde bewerking van de grootste gemene deler , hoewel deze met vergelijkbare methoden wordt berekend. Als je wilt leren hoe je de LCM kunt berekenen, raden we je aan verder te lezen, omdat we in dit artikel alle procedures (van de eenvoudigste tot de meest gecompliceerde) zullen uitleggen om het kleinste gemene veelvoud van een reeks getallen te vinden.

lcm rekenmachine

Voordat we beginnen te praten over hoe je lcm kunt krijgen, willen we dat je weet dat we op deze pagina een rekenmachine met de minste gemeenschappelijke veelvouden hebben. Hiermee kun je de lcm berekenen van alle gewenste getallen, op deze manier kun je de resultaten van je oefeningen vergelijken om te zien of je ze correct hebt opgelost.

Om de minder gebruikelijke meervoudige rekenmachine te gebruiken, voert u hele getallen in, gescheiden door een komma:

bereken lcm

Hoe bereken je het kleinste gemene veelvoud?

Om het kleinste gemene veelvoud van twee of meer getallen te vinden, moet je een van de drie methoden volgen die we hieronder zullen uitleggen. Wanneer we vervolgens elk van de procedures die u kunt kiezen gedetailleerd beschrijven, zullen we u ook vertellen wat hun voor- en nadelen zijn. Zo weet u per situatie welke u moet kiezen om de betreffende LCM eenvoudig en snel op te lossen.

Methode 1: Meerdere lijst

De eerste methode is het maken van een lijst met veelvouden van de getallen die u in de LCM wilt berekenen. Vervolgens moet je de kleinste waarde vinden die in alle lijsten wordt herhaald , op deze manier heb je het kleinste gemene veelvoud. Dan zullen we het zien met een voorbeeld: lcm (5, 6).

Methode 2: factoriële ontbinding

Ten tweede kunnen we ervoor kiezen om de getallen in factoren te ontbinden. Meer specifiek zal deze methode het gemakkelijker maken om de pcm van grote getallen te berekenen . Omdat het volgen van methode 1 bij het uitvoeren van lcm van grote getallen langzaam en vervelend kan zijn, simpelweg omdat we hele lange lijsten met veelvouden zullen moeten schrijven. Deze tweede procedure kan in het begin wat ingewikkelder zijn om te begrijpen, maar als je de werking begrijpt, heeft het veel voordelen vergeleken met de vorige. Dat gezegd hebbende, laten we eens kijken naar de te volgen procedure:

• Factoriële decompositie: de eerste stap zal zijn het ontleden van alle getallen die we in de LCM gaan opnemen in priemfactoren. Als u niet weet hoe u een getal factorieel moet ontbinden , raden wij u aan deze laatste link in te voeren. Daar vindt u eersteklas uitleg over hoe u getallen snel en efficiënt kunt vereenvoudigen.
• Maak één enkele wiskundige uitdrukking: Wanneer we alle getallen als priemfactoren hebben uitgedrukt, kiezen we de gewone en niet-gewone getallen, verheven tot de grootste exponent. Vervolgens schrijf je ze op als één wiskundige uitdrukking en tot slot los je de benodigde vermenigvuldigingen en/of machten op. En je hebt al de numerieke waarde van lcm.

Methode 3: Wiskundige formule

Er is een laatste manier om het kleinste gemene veelvoud te verkrijgen, die bestaat uit het gebruik van de GCD en de volgende wiskundige formule:

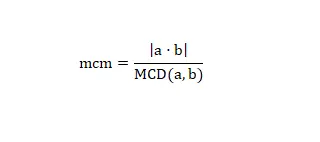
Met behulp van deze formule kunnen we de lcm van elk getal berekenen. Laten we een echt voorbeeld bekijken. Als we lcm (2,6) willen berekenen, hoeven we alleen maar de bewerking (2 x 6) / 2 = 6 op te lossen. En we hebben de berekening al opgelost, zoals je kunt zien is het een eenvoudige methode en snel als je de GCD hebt of deze eenvoudig kunt berekenen.

Tips om snel lcm te berekenen

Als je de drie methoden die we zojuist hebben uitgelegd onder de knie hebt, raden we je aan de eigenschappen van het kleinste gemene veelvoud te lezen waar we het nu over gaan hebben. Dankzij hen kunt u enkele specifieke situaties identificeren waarin de LCM zeer snel kan worden berekend, zonder dat u de reeds uitgelegde strategieën hoeft te gebruiken.

• Eerste getal deelbaar door het tweede: als we het kleinste gemene veelvoud van a en b willen berekenen wanneer a b deelt, dan zal de ppcm van deze twee getallen het grootste zijn (in dit geval b). Als u bijvoorbeeld de lcm van 2 en 8 wilt berekenen, is het resultaat het grootste, dus 8.
• Twee priemgetallen: Als u twee priemgetallen vindt, is de snelste methode om ze met elkaar te vermenigvuldigen. Het resultaat is de ppcm. Dit is logisch, aangezien de grootste gemene deler 1 is, wat betekent dat we het getal niet kunnen ontleden in eenvoudiger factoren dan het getal zelf, en dat we ze daarom alleen met elkaar kunnen vermenigvuldigen. De LCM van 3 en 5 is bijvoorbeeld het resultaat van hun product: 3 x 5 = 15.

Hoe krijg je het kleinste gemene veelvoud in breuken?

Als we breuken willen optellen of aftrekken, moeten we de kleinste gemene deler berekenen, die hetzelfde is als lcm, maar dan toegepast op breuken. In principe zoeken we naar de lcm van de twee noemers, zodat we de som vervolgens als één breuk kunnen uitdrukken. Als u wilt zien hoe de kleinste gemene deler wordt toegepast op een reële breukberekening, kunt u deze link invoeren.

Lcm op wetenschappelijke rekenmachine

Met de LCM-sleutel, die op elke wetenschappelijke rekenmachine te vinden is, kunt u het kleinste gemene veelvoud van twee gehele getallen berekenen. In het geval van Casio-rekenmachines is de syntaxis of procedure die u moet volgen als volgt. Eerst drukt u op APHA + MCM (deze laatste toets wordt bruin gemarkeerd). Zodra dit is gebeurd, kunt u beide cijfers invoeren, maar onthoud dat u ze moet scheiden met een komma ( SHIFT +, ). Ten slotte krijgt u het kleinste gemene veelvoud door op de knop 'is gelijk aan' te klikken.

LCM-oefeningen stap voor stap opgelost

Vervolgens laten we u stap voor stap drie voorbeelden zien van de opgeloste kleinste gemene veelvoud . Op deze manier kun je proberen deze problemen op te lossen en een beetje oefenen van wat we in dit artikel hebben uitgelegd. Het is belangrijk dat je de oefeningen probeert op te lossen als je de concepten wilt internaliseren, omdat het noodzakelijk is om de theorie op de werkelijkheid toe te passen. Dat gezegd hebbende, laten we je oefenen met de oefeningen:

Bereken de lcm van 4 en 6

Bereken de lcm van 6 en 9

Bereken de lcm van 30 en 40