In dit artikel leggen we uit wat begrensde (bovenste en onderste) functies zijn. Daarnaast laten we u zien wat het betekent als een functie op een punt wordt begrensd en tot slot vindt u de eigenschappen van dit type functie.
Wat is een begrensde functie?
Een begrensde functie is een functie waarvan de grafiek binnen bepaalde grenzen ligt. Dat wil zeggen, een functie wordt naar boven begrensd als er een getal K bestaat zodat er geen waarde van de functie groter is dan K (f(x)≤K), en een functie wordt naar beneden begrensd als er een getal K bestaat zodat het is kleiner dan alle waarden van de functie (f(x)≥K). Daarom is een begrensde functie een functie die boven en onder begrensd is.
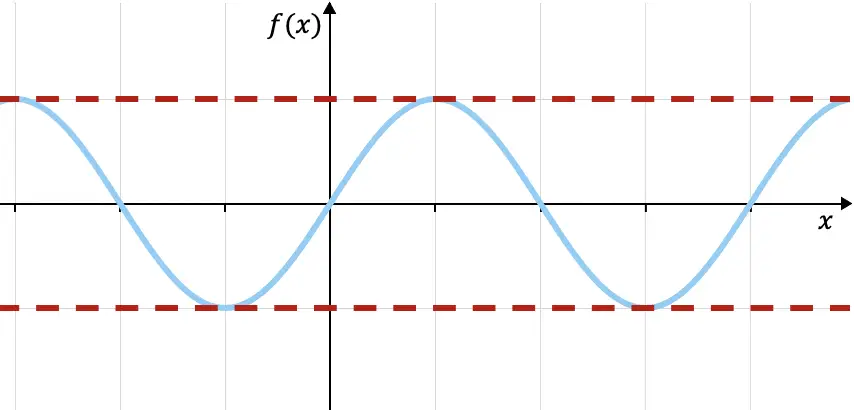
De trigonometrische sinusfunctie, hierboven weergegeven, wordt bijvoorbeeld bovenaan begrensd door f(x)=1 en onderaan begrensd door f(x)=-1 (rode stippellijnen), aangezien alle waarden van de functie liggen binnen deze twee grenzen. Meer eigenschappen van deze functie kunt u bekijken via de volgende link:
➤ Zie: Karakteristieken van de sinusfunctie
functie hierboven begrensd
Niet alle functies zijn echter boven en onder begrensd; een functie kan alleen boven of onder begrensd zijn.
De hierboven begrensde functies zijn functies die een bepaalde waarde niet overschrijden, dat wil zeggen dat aan de volgende voorwaarde is voldaan:
![]()
waarbij de waarde K de bovengrens van de functie is.
De volgende parabool wordt bijvoorbeeld bovenaan begrensd door K = 7, maar de functie wordt onderaan niet begrensd omdat de takken zich tot in het oneindige uitstrekken.

Logischerwijs wordt de functie, als deze wordt begrensd door K=7, ook begrensd door K=8 en hogere waarden.
De kleinste bovengrens wordt de bovengrens genoemd en wordt weergegeven door sup(f) . Bovendien, als de functie de bovengrens in zijn domein bereikt, zullen we zeggen dat dit punt het absolute maximum van de functie is.
➤ Zie: wat zijn de maxima en minima van een functie?
In ons geval wordt de functie geometrisch begrensd door K=7, het is daarom het bovenste uiterste en het absolute maximum van de functie.
hieronder afgebakende functie
De hieronder afgebakende functies zijn functies die geen waarde hebben die kleiner is dan een bepaald getal, dat wil zeggen dat ze voldoen aan de volgende wiskundige uitdrukking:
![]()
Waarbij de K-waarde de ondergrens van de functie is.
Hieronder ziet u de grafische weergave van een exponentiële functie die hieronder wordt begrensd door K=3:

Uiteraard wordt de functie ook begrensd door waarden kleiner dan K=3.
Net als voorheen wordt de grootste ondergrens de ondergrens genoemd en weergegeven door inf(f) . Bovendien, als de functie het onderste uiterste in zijn domein bereikt, zullen we zeggen dat dit punt het absolute minimum van de functie is.
In dit geval is K=3 niet het absolute minimum van de functie, omdat de functie deze waarde op oneindig bereikt en zich daarom buiten zijn domein bevindt. Met andere woorden, f(x)=3 is eenhorizontale asymptoot van de functie .
Er is een stelling waarmee je kunt weten of een functie aan de boven- en onderkant begrensd is zonder de grafische weergave ervan. Klik hier om te zien wat de stelling van Weierstrass is.
➤ Zie: Stelling van Weierstrass
Functie begrensd op één punt
We hebben zojuist het begrip begrenzing van een functie in het algemeen bestudeerd, maar het is ook mogelijk om te analyseren of een functie al dan niet wordt begrensd in een kleinere omgeving, dat wil zeggen in een deel van de functie.
Ja
![]()
is een punt in het domein van de functie en
![]()
welke waarde dan ook, we zullen zeggen dat de functie op het punt boven/onder begrensd is
![]()
als er een omgeving is
![]()
waarbij de functie boven/onder wordt begrensd.
Daarom is een functie begrensd op het punt
![]()
als deze in een buurt aan de boven- en onderkant is afgebakend
![]()
Als een functie in het algemeen begrensd is, zal deze uiteraard ook op elk van zijn punten begrensd worden. Het tegenovergestelde is echter niet waar, dat wil zeggen dat een functie op elk van zijn punten kan worden begrensd en niet op zijn hele domein.
De volgende affiene functie is bijvoorbeeld gedeeltelijk begrensd op elk van zijn punten, maar is geen begrensde functie.

Eigenschappen van begrensde functies
Begrensde functies hebben de volgende eigenschappen:
- Ja

En

zijn twee begrensde functies, de optelling (of aftrekking) van de twee functies
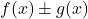
is ook een begrensde functie.
- Ja

En

zijn twee begrensde functies, het product van de twee functies
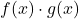
Het is ook een begrensde functie.
- Als een functie een verticale asymptoot heeft, kan deze niet volledig worden begrensd. Aan de andere kant kan de functie boven of onder worden begrensd.
- Elke continue en begrensde functie op een interval is integreerbaar.