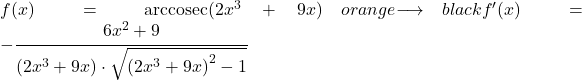Op deze pagina zie je wat de formule is voor de afgeleide van de arccosecant. Daarnaast kun je opgeloste oefeningen zien voor afgeleiden van de boog-cosecans van een functie.
Arccosecant-afgeleide formule
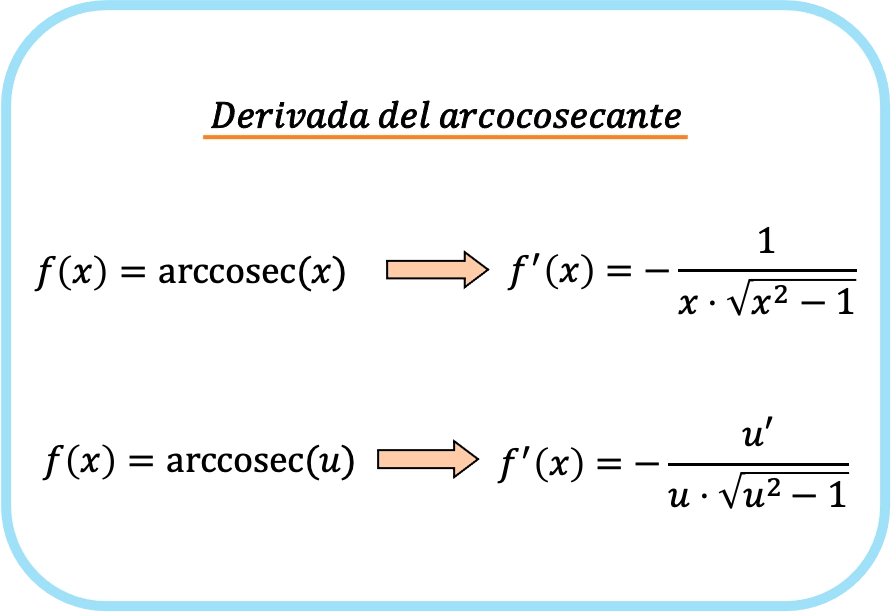
De afgeleide van de boogcosecans van x is negatief één over het product van x maal de wortel van x kwadraat minus 1.
![]()
Daarom is de afgeleide van de boogcosecans van een functie gelijk aan minus het quotiënt van de afgeleide van die functie gedeeld door de functie maal de wortel van die functie in het kwadraat min één.
![]()
In feite zijn de voorgaande twee formules hetzelfde, maar in de tweede uitdrukking wordt de kettingregel toegepast. Als je de identiteitsfunctie x in de u vervangt, krijg je in feite de afgeleide van de boogcosecans van x, aangezien de afgeleide van x één is.
Zoals u wel weet, is de boogcosecans de inverse trigonometrische functie van de cosecans, maar de afgeleiden ervan zijn heel verschillend. U kunt de formule voor dit andere type trigonometrische functie bekijken in de volgende link:
➤ Zie: afgeleide van de cosecans
Voorbeelden van afgeleide van de cosecante boog
Als we kijken wat de arccosecante afgeleide regel is, zullen we vervolgens twee voorbeelden van dit type afgeleide oplossen. Maar als u nog vragen heeft over het afleiden van de cosecansboog, kunt u ons deze in de opmerkingen stellen.
voorbeeld 1
In dit voorbeeld zullen we zien hoeveel de afgeleide is van de boogcosecans van de kwadratische functie x 2 .
![]()
Om de afgeleide van de boogcosecans van x kwadraat te berekenen, passen we de formule toe die we hierboven zagen:
![]()
De afgeleide van x tot de macht twee is 2x, dus de afgeleide van de samengestelde functie is:
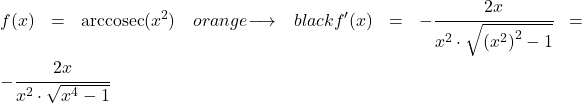
Voorbeeld 2
In dit tweede voorbeeld zullen we de boogcosecant van een potentiële functie afleiden.
![]()
We moeten de afgeleide regel van de boogsecant gebruiken om de afgeleide van de gehele functie te vinden.
![]()
Dus in de teller schrijven we de afgeleide van het argument van de functie, en in de noemer herschrijven we de potentiële functie en vermenigvuldigen we deze met de vierkantswortel van de functie van het argument in het kwadraat min 1: